
2.如图所示,物体甲、乙质量均为m。弹簧和悬线的质量可以忽略不计。当悬线被烧断的瞬间,甲、乙的加速度数值应是下列哪一种情况:
A.甲是0,乙是g B.甲是g,乙是g
C.甲是0,乙是0 D.甲是g/2,乙是g
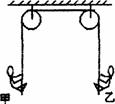 3.如图所示,一条质量不计的绳子跨过同一水平面的两个光滑的定滑轮,甲、乙两人质量相等,但甲的力气比乙大,他们各自握紧绳子的一端由静止同时在同一高度开始向上爬,并且两人在爬动过程中尽力爬,则 ( )
3.如图所示,一条质量不计的绳子跨过同一水平面的两个光滑的定滑轮,甲、乙两人质量相等,但甲的力气比乙大,他们各自握紧绳子的一端由静止同时在同一高度开始向上爬,并且两人在爬动过程中尽力爬,则 ( )
A.甲先到达顶端 B.乙先到达顶端
C.两人同时到达顶端 D.无法判断
 4.如图所示,车厢内用两根细绳AO、BO系住一个质量m的物体,AO绳与竖直方向间夹角为θ,BO是水平的,当车厢以加速度a水平向左作匀加速运动时,两绳中拉力T1、T2各是多少?
4.如图所示,车厢内用两根细绳AO、BO系住一个质量m的物体,AO绳与竖直方向间夹角为θ,BO是水平的,当车厢以加速度a水平向左作匀加速运动时,两绳中拉力T1、T2各是多少?
课后作业:
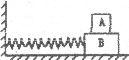 1.如图所示,质量为m的物体A放置在质量为M的物体B上,B与弹簧相连。它们一起在光滑水平面上作简谐振动。振动过程中A、B之无相对运动。设弹簧的劲度系数为k。当物体离开平衡位置的位移为x时,A、B间摩擦力的大小等于( )
1.如图所示,质量为m的物体A放置在质量为M的物体B上,B与弹簧相连。它们一起在光滑水平面上作简谐振动。振动过程中A、B之无相对运动。设弹簧的劲度系数为k。当物体离开平衡位置的位移为x时,A、B间摩擦力的大小等于( )
A.0 B.kx C.kmx/M D.kmx/(M+m)
2.几类问题的临界条件
(1)相互接触的两物体脱离的临界条件是相互作用的弹力为零,即N=0。
(2)绳子松弛的临界条件是绳中张力为零,即T=0。
(3)存在静摩擦的连接系统,相对静止与相对滑动的临界条件静摩擦力达最大值,即f静=fm。
 [例三]如图所示,质量为M的木板上放一质量为m的木块,木块与木板间的动摩擦因数为μ1;,木板和地面间的动摩擦因数为μ2,问加在木板上的力F多大时,才能将木板从木块和地面间抽出来?
[例三]如图所示,质量为M的木板上放一质量为m的木块,木块与木板间的动摩擦因数为μ1;,木板和地面间的动摩擦因数为μ2,问加在木板上的力F多大时,才能将木板从木块和地面间抽出来?
[例四]如图所示,质量为m的物体放在质量为M的倾角为α的斜面上,如果物体与斜面间、斜面体与地面间摩擦均不计,问
(1) 作用于斜面体上的水平力多大时,物体与斜面体刚好不发生相对运动?
 (2)此时m对M的压力多大?
(2)此时m对M的压力多大?
(3)此时地面对斜面体的支持力多大?
 [例五]如图所示,两光滑的梯形木块A和B,紧靠放在光滑水平面上,已知θ=60°,mA=2kg,mB=lkg,现水平推力F,使两木块使向右加速运动,要使两木块在运动过程中无相对滑动,则F的最大值多大?
[例五]如图所示,两光滑的梯形木块A和B,紧靠放在光滑水平面上,已知θ=60°,mA=2kg,mB=lkg,现水平推力F,使两木块使向右加速运动,要使两木块在运动过程中无相对滑动,则F的最大值多大?
课堂训练:
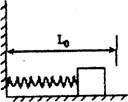 1.如图所示,在水平桌面上推一物体压缩一个原长为L0的轻弹簧。桌面与物体之间有摩擦,放手后物体被弹开,则( )
1.如图所示,在水平桌面上推一物体压缩一个原长为L0的轻弹簧。桌面与物体之间有摩擦,放手后物体被弹开,则( )
A.物体与弹簧分离时加速度为零,以后作匀减速运动
B.弹簧恢复到Lo时物体速度最大
 C.弹簧恢复到Lo以前一直作加速度越来越小的变加速运动
C.弹簧恢复到Lo以前一直作加速度越来越小的变加速运动
D.弹簧恢复到Lo以前的某一时刻物体已达到最大速度
1.在应用牛顿定律解决动力学问题中,当物体运动加速度不同时,物体有可能处于不同的状态,特别是题目中出现“最大”、“至少”、“刚好”等词语时,往往有临界现象,此时要采用极限分析法,看物体在不同加速度时,会有哪些现象发生,尽快找出临界点,求出临界条件。
3.在应用牛顿运动定律解题时,经常会遇到绳、杆、弹簧和橡皮条(绳)这些力学中常见的模型。全面、准确地理解它们的特点,可帮助我们灵活、正确地分析问题。
共同点
(1)都是质量可略去不计的理想化模型。
(2)都会发生形变而产生弹力。
(3)同一时刻内部弹力处处相同,且与运动状态无关。
不同点
(1)绳(或线):只能产生拉力,且方向一定沿着绳子背离受力物体;不能承受压力;认为绳子不可伸长,即无论绳所受拉力多大,长度不变。绳的弹力可以突变:瞬间产生,瞬间消失。
(2)杆:既可承受拉力,又可承受压力;施力或受力方向不一定沿着杆的轴向。
(3)弹簧:既可承受拉力,又可承受压力,力的方向沿弹簧的轴线。受力后发生较大形变;弹簧的长度既可以变长(比原来长度大),又可以变短。其弹力F与形变量(较之原长伸长或缩短的长度)x的关系遵守胡克定律F=kx(k为弹簧的劲度系数)。弹力不能突变(因形变量较大,产生形变或使形变消失都有一个过程),故在极短时间内可认为形变量和弹力不变。当弹簧被剪断时,其所受弹力立即消失。
(4)橡皮条(绳):只能受拉力,不能承受压力(因能弯曲)。其长度只能变长(拉
伸)不能变短.受力后会发生较大形变(伸长),其所受弹力F与其伸长量x的关系遵从胡克定律F=kx。弹力不能突变,在极短时间内可认为形变量和弹力不变。当被剪断时,弹力立即消失。
[例一]一轻弹簧上端固定,下端挂一重物,平衡时弹簧伸长了4cm,再将重物向下拉lcm,然后放手,则在刚释放的瞬间重物的加速度是(g=l0m/s2) ( )
A.2.5 m/s2 B.7.5 m/s2 C.10 m/s2 D.12.5 m/s2
 [例二]如图所示,自由下落的小球开始接触竖直放置的弹簧到弹簧被压缩到最短的过程中,小球的速度和所受合力的变化情况是( )
[例二]如图所示,自由下落的小球开始接触竖直放置的弹簧到弹簧被压缩到最短的过程中,小球的速度和所受合力的变化情况是( )
A.合力变小,速度变小
B.合力变小,速度变大
C.合力先变小后变大,速度先变大后变小
D.合力先变小后变大,速度先变小后变大
2.分析物体在某一时刻的瞬时加速度,关键是分析瞬时状态前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度,此类问题应注意两种基本模型的建立。
(1)钢性绳(或接触面):认为是一种不发生明显形变就可产生弹力的物体,若剪断(或脱离)后,其弹力立即消失,不需要形变恢复时间,一般题目中所给的细线和接触面在不加特殊说明时,均可按此模型处理。
(2)弹簧(或橡皮绳):此种物体的特点是形变量大,形变恢复需要较长时间,在瞬时问题中,其弹力的大小往往可以看成不变。
1.在动力学问题中,物体受力情况在某些时候会发生突变,根据牛顿第二定律的瞬时性,物体受力发生突变时,物体的加速度也会发生突变,突变时刻物体的状态称为瞬时状态,动力学中常常需要对瞬时状态的加速度进行分析求解。
15. 如图4-41所示,一个载货小车总质量为50kg,静止在水平地面上.现用大小为300N,跟水平方向成30°角斜向上的拉力拉动货车,做匀加速运动0.4s后撤去拉力,在经5s车的速度多大?货车运动的位移最大是多少?(已知
如图4-41所示,一个载货小车总质量为50kg,静止在水平地面上.现用大小为300N,跟水平方向成30°角斜向上的拉力拉动货车,做匀加速运动0.4s后撤去拉力,在经5s车的速度多大?货车运动的位移最大是多少?(已知 =0.1)
=0.1)
14.为了安全,在公路上行驶的汽车之间应保持必要的距离.已知某高速公路的最高限速 v=120km/h,假设前方车辆突然停下,后车司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s.刹车时汽车受到阻力的大小f为汽车重力的0.40倍,该高速公路上汽车间的距离s至少应为多少?g取10m/s2).
13.竖直升降的电梯内的天花板上悬挂着一根弹簧秤,如图4-40所示,弹簧秤的称钩上悬挂着一个质量为4kg的物体,试分析下列情况下电梯的运动情况:(g取10m/s2 )
 (1).当弹簧秤的实施FT1=40N,且保持不变.
(1).当弹簧秤的实施FT1=40N,且保持不变.
(2).当弹簧秤的实施FT2=32N,且保持不变.
(3).当弹簧秤的实施FT3=44N,且保持不变.
12.某人在以2.5 m/s2的加速度匀加速下降的升降机里最多能举起80kg的物体,他在地面上最多能举起 kg 的物体;若此人在一匀加速上升的升降机里最多能举起40kg的物体,则次升降机上升的加速度为 m/s2 .(g取10m/s2).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com