
2.如图所示,物体A置于物体B上,一轻质弹簧一端固定,另一端与B相连.在弹性限度范围内,A和B一起在光滑水平面上作往复运动(不计空气阻力),并保持相对静止.则下列说法正确的是
(A)A和B均作简谐运动
(B)作用在A上的静摩擦力大小与弹簧的形变量成正比
(C)B对A的静摩擦力对A做功,而A对B的静摩擦力对B不做功
(D)B对A的静摩擦力始终对A做正功,而A对B的静摩擦力始终对B做负功

1.木块A、B分别重50 N和60 N,它们与水平地面之间的动摩擦因数均为0.25。夹在A、B之间的轻弹簧被压缩了2 cm,弹簧的劲度系数为400 N/m。系统置于水平地面上静止不动。现用F=1 N的水平拉力作用在木块B上,如图所示。力F作用后

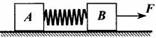 A.木块A所受摩擦力大小是12.5
N
A.木块A所受摩擦力大小是12.5
N
B.木块A所受摩擦力大小是11.5 N
 C.木块B所受摩擦力大小是9
N
C.木块B所受摩擦力大小是9
N
D.木块B所受摩擦力大小是7 N

2.方程: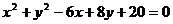 的曲线是什么图形?
的曲线是什么图形?
教学设计说明
圆是学生比较熟悉的曲线,初中平面几何对圆的基本性质作了比较系统的研究,因此这节课的重点确定为用解析法研究圆的标准方程及其简单应用。.首先,在已有圆的定义和求曲线方程的一般步骤的基础上,用实际问题引导学生探究获得圆的标准方程,然后,利用圆的标准方程由浅入深的解决问题,并通过圆的方程在实际问题中的应用,增强学生用数学的意识。另外,为了培养学生的理性思维,我分别在引例和问题四中,设计了两次由特殊到一般的学习思路,培养学生的归纳概括能力。在问题的设计中,我用一题多解的探究,纵向挖掘知识深度,横向加强知识间的联系,培养了学生的创新精神,并且使学生的有效思维量加大,随时对所学知识和方法产生有意注意,能力与知识的形成相伴而行,这样的设计不但突出了重点,更使难点的突破水到渠成.
本节课的设计了五个环节,以问题为纽带,以探究活动为载体,使学生在问题的指引下、教师的指导下把探究活动层层展开、步步深入,充分体现以教师为主导,以学生为主体的指导思想。应用启发式的教学方法把学生学习知识的过程转变为学生观察问题、发现问题、分析问题、解决问题的过程,在解决问题的同时锻炼了思维.提高了能力、培养了兴趣、增强了信心。
3.激发新疑:
问题七:1.把圆的标准方程展开后是什么形式?
2.分层作业:(A)巩固型作业:课本P81-82:(习题7.6)1.2.4
(B)思维拓展型作业:
试推导过圆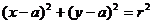 上一点
上一点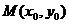 的切线方程.
的切线方程.
1.课堂小结:
(1)圆心为C(a,b),半径为r 的圆的标准方程为: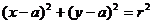
当圆心在原点时,圆的标准方程为:
(2) 求圆的方程的方法:①找出圆心和半径;②待定系数法
(3) 已知圆的方程是 ,经过圆上一点
,经过圆上一点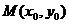 的切线的方程是:
的切线的方程是:
(4) 求解应用问题的一般方法
4.已知圆的方程为 ,求过点
,求过点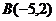 的切线方程.
的切线方程.
3.求圆x2+y2=13过点(-2,3)的切线方程.
问题六:1.求以C(-1,-5)为圆心,并且和y轴相切的圆的方程.
2.已知点A(-4,-5),B(6,-1),求以AB为直径的圆的方程.
3.你能归纳出具有一般性的结论吗?
已知圆的方程是 ,经过圆上一点
,经过圆上一点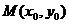 的切线的方程是:
的切线的方程是: .
.
III.实际应用(回归自然)
问题五:如图是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱 的长度(精确到0.01m).
的长度(精确到0.01m).
[多媒体课件演示创设实际问题情境]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com