
9、某工人原计划每天生产a个零件,现实际每天多生产b个零件,则生产m个零件提前的天数为( )。
A、 B、
B、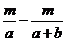
 C、
C、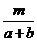 D、
D、
8、某商人在一次买卖中均以120元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )。
A、赚16元 B、赔16元 C、不赚不赔 D、无法确定
7、某市举行的青年歌手大奖赛今年共有a人参加,比赛的人数比去年增加 20%还多3人,设去年参赛的人数为x人,则x为( )。
A、 B、
B、 C、
C、  D、
D、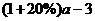
6、国家规定工职人员每月工资超出800元以上部分缴纳个人所得税的20%,小英的母亲10月份交纳了45.89的税,小英母亲10月份的工资是( )。
A、8045.49元  B、1027.45元 C、1227.45元 D、1045.9元
B、1027.45元 C、1227.45元 D、1045.9元
5、方 程
程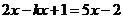 的解为-1时,k的值为( )。
的解为-1时,k的值为( )。
A、10 B、-4 C、-6 D、-8
4、三个正整数的比是1:2:4,它们的和是84,那么这三个数中最大的数是( )。
A、56 B、48 C、36 D、12
3、解方程 时,把分母化为整
时,把分母化为整 数,得( )。
数,得( )。
A、 B、
B、
C、 D、
D、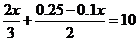
2、根据“x的3倍与5的和比x的 多2”可列方程( )。
多2”可列方程( )。
A、 B、
B、 C、
C、 D、
D、
1、下列各式中是一元一次方程的是( )。
A、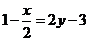 B、
B、 C、
C、 D、
D、
3.一元一次方程的应用。
知识梳理
知识点1:等式及其性质
重点:等式的基本性质的理解
难点:性质的运用
等式及其性质 ⑴ 等式:用等号“=”来表示 关系的式子叫等式.
⑵ 性质:① 如果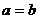 ,那么
,那么 ;
;
② 如果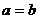 ,那么
,那么 ;如果
;如果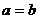
 ,那么
,那么 .
.
例:已知等式 ,则下列等式中不一定成立的是( )
,则下列等式中不一定成立的是( )
(A) (B)
(B)
(C) (D)
(D)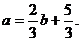
解题思路:利用等式的性质(1)两边都减去5,则A正确;利用性质(1)两边 都加1,则B正确;性质(2)两边都除以3,则D正确,故选C
都加1,则B正确;性质(2)两边都除以3,则D正确,故选C
知识点2:一元一次方程的概念
重点:一元一次方程的概念
难点:正确理解概念
⑴ 方程:含有未知数的  叫做方程;使方程左右两边值相等的 ,叫做方程的解;求方程解的 叫做解方程. 方程的解与解方程不同.
叫做方程;使方程左右两边值相等的 ,叫做方程的解;求方程解的 叫做解方程. 方程的解与解方程不同.
⑵ 一元一次方程:在整式方程中,只含有 个未知数,并且未知数的次数是 ,系数不等于0的方程叫做一元一次方程;它的一般形式为
 .
.
例1、下列各式:①3x+2y=1②m-3=6③x/2+2/3=0.5④x2+1=2⑤z/3-6=5z⑥(3x-3)/3=4⑦5/x+2=1⑧x+5中,一元一次方程的个数是( )
A、1 B、2 C、3 D、4
分析:根据一元一次方程定义,化简后具备以下五个条件:①含有一个未知数②未知数的次数为一次③未知数的系数不为0④分母中不含有未知数⑤是等式,才是一元一次方程.这些条件缺一不可,所以根据上述要求可以确定答案为D.
例2、 如果(m-1)x|m| +5=0是一元一次方程,那么m=___.
分析:此题是依据一元一次方程的定义来解决问题的,要使(m-1)x|m| +5=0是一元一次方程,则必须使|m|=1且m-1≠0,从而确定m=-1
知识点3: 解一元一次方程
重点:解一元一次方程的步骤
难点:熟练解方程
解一元一次方程的步骤:
①去 ;②去 ;③移 ;④合并 ;⑤系数化为1.
例1、要解方程4.5(x+0.7)=9x ,最简便的方法应该首先( )
A、去括号 B、移项 C、方程两边同时乘以10 D、方程两边同时除以4.5
分析:由于9是4.5的2倍,所以选择D最简便.
例2、解方程
分析:此题的常规解法是去分母,但是我们看到括号内的分母正好是括号外数字的公约数,所以我们直接去括号即可以达到求解目的.
解:去括号 8x-20x+6 =8-4x+6
移项 8x-20x+4x=8+6 -6
-6
合并 -8x=8
系数化为1 x=-1
知识点4:一元一次方程的实际应用
重点:找等量关系列方程
难点:审题找准等量关系,巧妙设未知量
例1、王老师去集贸市场买鸡蛋,小贩称好以后,王老师发现所买的10斤鸡蛋好象比原来少了一些,于是王老师就把鸡蛋拾进了自己的篮子{已知篮子重一斤}里又让小贩称了一下,结果是11斤1两,于是王老师就让小贩找回自己一斤鸡蛋钱,你知道王老师是怎么知道小贩少给自己一斤鸡蛋的吗?
分析:解决问题的关键因素--篮子:为什么不用篮子正好是10斤,而用了篮子就是11斤1两呢?这就是说小贩的称出了问题:一斤的篮子被称成了一斤一两。从而可设小贩称的10斤鸡蛋的实际质量是x斤,由题意分析可知:x:10=1:1.1, 所以x=10:11≈9.09{斤}。也就是说小贩称的10斤鸡蛋实际上约有9.09斤,所以王老师的做法是对的
例2、某校初三年级学生参加社会实践活动,原计划租用30座客车若干辆,但还有15人无座位。
(1)设原计划租用30座客车x辆,试用含x的代数式表示该校初三年级学生的总人数;
(2)现决定租用40座客车,则可比原计划租30座客车少一辆,且所租40座客车中有一辆没有坐满,只坐35人。请你求出该校初三年级学生的总人数。
分析:本题表示初三年级总人数有两种方案,用30座客车的辆数表示总人数:30x+15
用40座客车的辆数表示总人数:40(x-2)+35。
解:(1)该校初三年级学生的总人数为:30x+15
(2)由题意得:
30x+15=40(x-2)+35
解得:x=6
30x+15=30×6+15=195(人)
答:初三年级总共195人。
最新考题
一元一次方程是中考重点内容之一,其中主要以填空、选择形式出现,列一元一次方程解决简单的实际问题是很多省市每年必考内容。分值大约占15分左右,解决实际问题中考考查的主要方向。
中考课标要求
|
考点 |
课标要求 |
知识与技能目标 |
|||
|
了解 |
理解 |
掌握 |
灵活应用 |
||
|
一元一次方程 |
了解方程、一元一次方程以及方程有解的概念 |
∨ |
|
|
|
|
会解一元一次方程,并能灵活应用 |
∨ |
|
∨ |
∨ |
|
|
会列一元一次方程解应用题,并能根据问题的实际意义检验所得结果是否合理。 |
|
∨ |
∨ |
∨ |
考查目标一 方程解的应用
例1(2009·芜湖)已知方程3x -9x+m=0的一个根是1,则m的值是 。
-9x+m=0的一个根是1,则m的值是 。
解题思路:根据方程解的定义,把方程的解x=1代入方程成立,然后解决关于m的方程即可,
解:把x=1代入原方程,得3× -9×1+m=0,
-9×1+m=0,
 解得m=6
解得m=6
答案:6
点评:解题 依据是方程解的定义,解题方法是把方程的解代入原方程,转化为关于待定系数的方程。
依据是方程解的定义,解题方法是把方程的解代入原方程,转化为关于待定系数的方程。
考查目标二 巧 解一元一次方程
解一元一次方程
例2(2008·江苏)解方程:
解题思路:此题先用分配律简化方程,再解就容易了。
解:去括号,得
移项、合并同类项,得-x=6 ,
,
系数化为1,得x=-6
点评:解一元一次方程,掌握步骤,注意观察特点,寻找解题技巧,灵活运用分配委或分数基本性质等,使方程简化。
考查目标三 根据方程ax=b解的情况,求待定系数的值
例3已知关于x的方程 无解,则a的值是(
)
无解,则a的值是(
)
A.1 B.-1 C.±1 D.不等于1的数
解题思路:需先化成最简形式,再根据无解的条件,列出a的等式或不等式,从而求出a的值。
解:去分母,得2x+6a=3x-x+6,
即0·x=6-6a
因为原方程无解,所以有6-6a≠0,
即a≠1,
答案:D
考查目标四 一元一次方程的应用
例4(2009·福州)某班学生为希望工程共捐款131元,比每人平均2 元还多35元,设这个班的学生有x人,根据题意列方程为_________________。
解题思路:本题的相等关系是捐款总数相等,解决此题的关键是用学生人数、平均数与余数35元表示出捐款总数(2x+35)元。
答案:2x+35=131
过关检测
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com