5. 在图3所示的电路中，闭合开关S，能用电压表测量L₁两端电压的正确电路是

4. 如图2所示，当开关S闭合时，两只小灯泡能同时发光的正确电路是

3. 如图1所示，将一块砖平放、立放、侧放时，它对地面的压强

A.平放时最大

B.立放时最大

C.侧放时最大

D.平放、立放、侧放时，一样大

2. 发现有人触电后，应采取的正确措施是

A.赶快把触电人拉离电源　　　　　　　　　　　　 B.赶快去叫医护人员来处理

C.赶快切断电源或用干燥的木棒将电线挑开　　　　 D.赶快用剪刀剪断电源线

只有一项是正确的。)

1. 下列现象中不能说明分子在做无规则运动的是

A.春暖花开时，能闻到花的香味　　　　　 　B.打开酒瓶盖能闻到酒的气味

C.空气中飘动的浮尘　　　　 D.在盛有热水的杯子中放几片茶叶，过一会整杯水都变成茶水

3.解(1)对两小球整体由牛顿第二定律有

　①(4分)

　 (2) 小球沿F方向的位移随时间变化的关系式为S=kt²(k为恒量) ∴是匀加速运动

　　　　 ②　　 (4分)

　 (3) 根据功能原理：

③

　 (4分)

　 (4)假设在拉力作用的前2s内两球未发生碰撞，在2s时，小球沿F方向的分速度为,垂直于F方向的分速度为

　　　 根据动能定理：

　　　　 ④　　 (2分)

　　 　　⑤　　　　　　 ⑥　　　　　 解④、⑤、⑥得：　　　　 ∵每次碰撞后小球垂直于F方向的速度将损失0.3m/s

∴(次)≈4次　

3．(16分)如图所示,两个相同的质量m=0.2kg的小球用长L=0.22m的细绳连接,放在倾角为

30º的光滑斜面上.初始时刻,细绳拉直,且绳与斜面底边平行.在绳的中点作用一个垂直于绳沿斜面向上的恒力F=2.2N.在F的作用下两小球向上运动，小球沿F方向的位移随时间变化的关系式为s=kt²(k为恒量)。经过一段时间两个小球第一次碰撞,又经过一段时间再一次发生碰撞…….由于两小球之间有粘性,每一次碰撞后, 小球垂直于F方向的速度都将损失0.3m/s.当力F作用了2s时,两小球发生最后一次碰撞,且不再分开.取g=10m/s²,求:

(1)最后一次碰撞后,小球的加速度

(2)最后一次碰撞后瞬间,小球的速度

(3)整个碰撞过程中,系统损失的机械能

(4)两小球相碰的总次数

2.如图所示，光滑水平面右端B处连接一个竖直的半径为R的光滑半圆轨道，B点为水平面与轨道的切点，在离B距离为x的A点，用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力，质点沿半圆轨道运动到C处后又正好落回A点：

(1) 求推力对小球所做的功。

(2) x取何值时，完成上述运动推力所做的功最少?最小功为多少。

(3) x取何值时，完成上述运动推力最小?最小推力为多少。

2解:(1)质点从半圆弧轨道做平抛运动又回到A点，设质点在C点的速度为v_C，质点从C点运动到A点所用的时间为t，

在水平方向：　 x=v_Ct　　　　　　　　　　　　　 ①　　　

竖直方向上：2R=gt²②　　　

解①②有　 v_C=　　　　　　　　　　　　 ③　　　　

　 对质点从A到C由动能定理有

W_F-mg·2R=mv　　　　　　　　　　　　　　　 ④　　　　

解W_F=mg(16R²+x²)/8R　　　　　　　　　　　　 　⑤ 　　　

(2)要使F力做功最少，确定x的取值，由W_F=2mgR+mv知，只要质点在C点速度最小，则功W_F就最小。若质点恰好能通过C点，其在C点最小速度为v，由牛顿第二定律有

mg=,则v=　　　　　　　　　　 　　⑥　　 　　

由③⑥有=,解得：x=2R　　　　　　　　　 ⑦　　　

当x=2R时， W_F最小，最小的功：W_F=mgR　　　　 ⑧

(3)由⑤式W_F=mg() 及W_F=F x 　 得：F=mg()　 　　⑨　 　　　　　　　　　　　　　　　　　　　　　　　　　　

　 F 有最小值的条件是： =、即x=4R　　　 　　　　　⑩

由⑨⑩得最小推力为：F=mg　　　　 　　　　　　　⑾

7：(1)从A到B的过程中，人与雪橇损失的机械能为：

　　　　　　 　①

代入数据解得：ΔE ＝9100J　　

(2)人与雪橇在BC段做减速运动的加速度： ②

　　　　 根据牛顿第二定律：　 ③　　

由②③ 得：140N　　　　　　　　

(3)由动能定理得：　 代入数据解得：36m

8:(1)在t秒内，通过发电机的水的质量是：m=ρV

　用来发电的水的势能是：E_p=mgh　　 发电机电功率：p=E_P*20%/t=1.35*10⁹W．

(2)每天的发电量：E=pt=3.24×10⁷ kW.h

每个家庭的用电量：E_o=(0.7×0.6 + O.05×24 + 0.2×2 + 0.24×4) kW.h = 2.98 kW.h

以每个家庭三口人计算，800万人口的城市家庭用电：E₁=8×10⁶÷3 x2.98kW.h=8×10⁶ kW.h　 可以供电的城市个数是N=E/E₁=3.24×10⁷/8×10⁶=4

　 　　易错点：①计算势能时，水的重心在135/2 m处，而不是135m处。②100万人口只有近33万个家庭。③应以天计算供电量，而不是计算电功率。

9：①将F沿水平方向、竖直方向分解，冰块受的支持力　

　 摩擦力　

　 在前一阶段，对冰块由动能定理：

　 联立以上各式，并将x₁=4.00m等代入，解出υ₁=1.00m/s．　

　 ②冰块做类平抛运动，沿x轴方向　　 ．

　 沿Y轴方向，由牛顿第二定律：　　

　 　。　　

　 联立解出y=52.0m>5m，故冰块碰不到仪器室．　

10:(1)由图象可得，在14s-18s时间内：

阻力大小：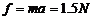

(2)在10s--14s内小车做匀速运动：

故小车功率：

(3)速度图象与时间轴的“面积”的数值等于物体位移大小：

0-2s内，

2s-10s内，根据动能定理有：

解得：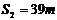

故小车在加速过程中的位移为：

备选题：

1．如图所示，竖直平面内的3/4圆弧形光滑轨道半径为R，A端与圆心O等高，AD为水平面，B端在O的正上方，一个小球在A点正上方由静止释放，自由下落至A点进入圆轨道并恰能到达B点．

求：(1)释放点距A点的竖直高度；

　 (2)落点C与O点的水平距离．

1解：(1)设小球距A点高为h处下落，到达B点时速度大小为v_B．小球下落过程只有重力做功，故小球由最高点经A运动B点过程中机械能守恒：

　　 ①　

由圆周运动规律可知，小球恰能达到B点的最小速度的条件为：

　　　　 　②　　

由①②解得：　　　　

(2)设小球由B点运动到C点所用的时间为t，小球离开B点后做平抛运动，设落点C与O点的水平距离为S，则有：

　　　　　　 ③　　　　　　　　　　　　 　　　　　④　

　由②③④解得：　　　 ………2分

10．某兴趣小组对一辆自制小遥控车的性能进行研究。他们让这辆小车在水平的直轨道上由静止开始运动，并将小车运动的全过程记录下来，通过处理转化为v-t图象，如图所示(除2s-10s时间段内的图象为曲线外，其余时间段图象均为直线)。已知小车运动的过程中，2s-14s时间段内小车的功率保持不变，在14s末停止遥控而让小车自由滑行。小车的质量为1kg，可认为在整个过程中小车所受到的阻力大小不变。求：

(1)小车所受到的阻力大小；

(2)小车匀速行驶阶段的功率；

(3)小车在加速运动过程中位移的大小。

机械能综合应用答案

典型例题：

例1．(1)加速过程在B点结束，即此后沿平直路面作匀速直线运动

　　 由牛顿第二定律和图象可得

　　 F_B-f=0……………①

　　 F_B=10⁴N…………②

　　 f=10⁴N……　 ……③

　　 (2)由图象、功率与功的关系和功能原理可得

　　 P=Fv…………④　　　 　　　W=pt…………⑤

　　　　 W-Fs=mv²………⑥　 　　　

例2：(1)由于小孩无碰撞进入圆弧轨道，即小孩落到A点时速度方向沿A点切线方向，则 　　又由　 得

　　　　 而　 　　联立以上各式得

　 (2)设小孩到最低点的速度为，由机械能守恒，有

　 　　在最低点，据牛顿第二定律，有　

代入数据解得F_N=1290N　 由牛顿第三定律可知，小孩对轨道的压力为1290N．

例3：(共12分) 第一过程A、B、C三物体一起做匀加速运动，第二过程A、B一起做匀减速运动。设A与水平面间的动摩擦因数为μ，设C即将碰D的瞬间速度为v，则第一过程的末速度即第二过程的初速度　　

根据动能定理：在第一过程中，对A、B、C组成的系统有：

(m_B+m_c)gh₁-μm_Agh₁＝(m_A+m_B+m_C)v²/2　 ……(4分)

在第二过程，对A、B组成的系统有：

m_Bgh₂一μm_Agh₂＝0一(m_A+m_B)v²／2　 ……(4分)

　　 代人数据解得μ=0.2　 　……(2分)

例4：(1)(6分)对A由动能定理：　　 (1)

解得；A与B相碰后速度交换。

故第一次相碰后，A速度为零；B速度为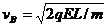　 (2)

(2)(6分)从A开始运动到碰第一次历时t₁=

设第二次碰前A速为 ，从第一次碰后到第二次碰前历时t₂

对A、由动能定理：　　　 (3)　　

　(4)　　 (2分)由(3)、(4)两式得：

故两球第二次碰时经历的时间为：　 (5)　

(3)(8分)由(3)(4)两式解得：

　　 此时B的速度为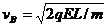

第二次碰后速度再交换。由速度图像也可得到第三次碰前A速度

　 　　　 (6)　　

此时B的速度为 (7)

依此类推第n次碰前A速度为：

　 (8)　　

　 故第n次与第n+1次碰撞经历时间为：

　 (9)　

　第n次碰后B以速度匀速运动，

故该时间内A通过的路程为：　 (10)　

针对训练：