
4.D
根据倒数第二段:How do you make believable wild animals, that aren't real? 这一句话可以得出答案。
3.C
根据最后一段最一句话可以得出答案。
2.C
根据倒数第三段和最后一段最一句话可以得出答案。
1.C
本题主要介绍了迪斯尼乐园是如何建成的展开论述。A、B两项片面,D项范围太大。
5. The underlined phrase in the last paragraph probably means _________.
A. collect B. improve C. find D. open
[答案解析]
4. You could see all the following things except_________ in Disney.
A. rivers, waterfalls, and mountains B. flying elephants and giant teacups
C. a huge castle D. wild animals
3. Which of the following statements is Not True?
A. World War II had some influence on the building plan of the Disneyland.
B. Disney must have met many difficulties in building Disneyland.
C. About 50 million visitors have visited Disneyland so far.
D. Disney was a great man with great imagination and creativity.
2. Which of the following dates would probably be the opening date of Disneyland?
A. 1953 B. 1954 C. 1955 D. 1965
1. The passage is mainly about___________.
A. What visitors can enjoy in Disneyland.
B. The difficulties Disney met in building Disneyland
C. How Disneyland came into being
D. A brief introduction to Disneyland
1.4.1曲边梯形的面积与定积分
|
学习目标: 1.理解求曲边图形面积的过程:分割、以直代曲、逼近,感受在其过程中渗透的思想方法;2.借助于几何直观定积分的基本思想,理解定积分的概念; 3. 理解掌握定积分的几何意义. 学习难点重点: 定积分的概念、定积分法求简单的定积分、定积分的几何意义 自主学习: 一、知识再现:导数的概念及应用 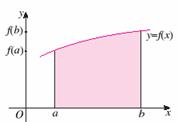 二、新课探究: 二、新课探究:提出问题 如图,阴影部分类似于一个梯形,但有一边是曲线 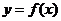 的一段,我们把由直线 的一段,我们把由直线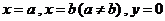 和曲线 和曲线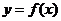 所围成的图形称为曲边梯形.如何计算这个曲边梯形的面积? 所围成的图形称为曲边梯形.如何计算这个曲边梯形的面积? 例题分析: 求图中阴影部分是由抛物线  ,直线 ,直线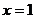 以及 以及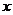 轴所围成的平面图形的面积S. 轴所围成的平面图形的面积S. (1).分割 在区间 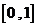 上等间隔地插入 上等间隔地插入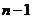 个点,将区间 个点,将区间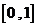 等分成 等分成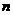 个小区间: 个小区间: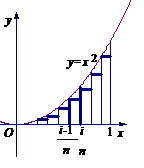 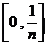 , , ,…, ,…,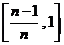 记第 记第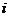 个区间为 个区间为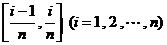 ,其长度为 ,其长度为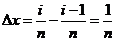 分别过上述 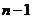 个分点作 个分点作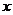 轴的垂线,从而得到 轴的垂线,从而得到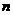 个小曲边梯形,他们的面积分别记作: 个小曲边梯形,他们的面积分别记作: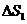 , , ,…, ,…,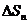 显然, 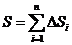 (2)近似代替 记 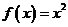 ,如图所示,当 ,如图所示,当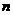 很大,即 很大,即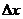 很小时,在区间 很小时,在区间 上,可以认为函数 上,可以认为函数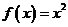 的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点 的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点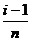 处的函数值 处的函数值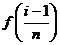 ,从图形上看,就是用平行于 ,从图形上看,就是用平行于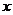 轴的直线段近似的代替小曲边梯形的曲边(如图).这样,在区间 轴的直线段近似的代替小曲边梯形的曲边(如图).这样,在区间 上,用小矩形的面积 上,用小矩形的面积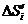 近似的代替 近似的代替 ,即在局部范围内“以直代取”,则有 ,即在局部范围内“以直代取”,则有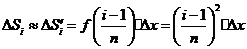 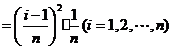 ① ①(3)求和 由①,上图中阴影部分的面积  为 为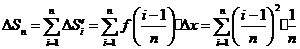 = 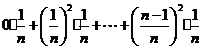 = =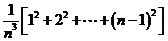 = 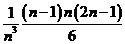 = =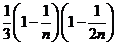 从而得到 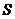 的近似值 的近似值 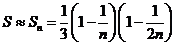 (4)取极限 分别将区间 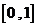 等分8,16,20,…等份(如图),可以看到,当 等分8,16,20,…等份(如图),可以看到,当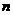 趋向于无穷大时,即 趋向于无穷大时,即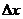 趋向于0时, 趋向于0时,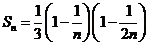 趋向于 趋向于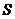 ,从而有 ,从而有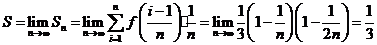 归纳总结: 求曲边梯形面积的四个步骤: 第一步:分割.在区间 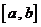 中任意插入 中任意插入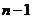 各分点,将它们等分成 各分点,将它们等分成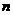 个小区间 个小区间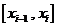 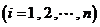 ,区间 ,区间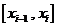 的长度 的长度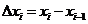 , ,第二步:近似代替,“以直代取”。用矩形的面积近似代替小曲边梯形的面积,求出每个小曲边梯形面积的近似值. 第三步:求和. 第四步:取极限。 定积分的概念 一般地,设函数 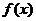 在区间 在区间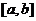 上连续,用分点 上连续,用分点 将区间 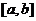 等分成 等分成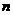 个小区间,每个小区间长度为 个小区间,每个小区间长度为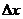 ( (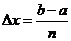 ),在每个小区间 ),在每个小区间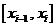 上取一点 上取一点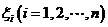 ,作和式: ,作和式: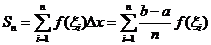 如果 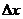 无限接近于 无限接近于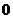 (亦即 (亦即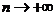 )时,上述和式 )时,上述和式 无限趋近于常数 无限趋近于常数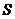 ,那么称该常数 ,那么称该常数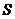 为函数 为函数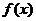 在区间 在区间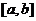 上的定积分。记为: 上的定积分。记为: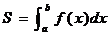 ,其中 ,其中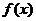 成为被积函数, 成为被积函数,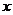 叫做积分变量, 叫做积分变量,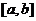 为积分区间, 为积分区间, 积分上限, 积分上限,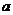 积分下限。 积分下限。定积分的几何意义 如果在区间 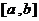 上函数连续且恒有 上函数连续且恒有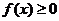 ,那么定积分 ,那么定积分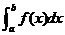 表示由直线 表示由直线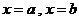 ( (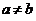 ), ),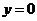 和曲线 和曲线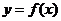 所围成的曲边梯形的面积。 所围成的曲边梯形的面积。说明:一般情况下,定积分 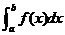 的几何意义是介于 的几何意义是介于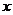 轴、函数 轴、函数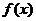 的图形以及直线 的图形以及直线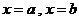 之间各部分面积的代数和,在 之间各部分面积的代数和,在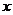 轴上方的面积取正号,在 轴上方的面积取正号,在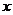 轴下方的面积去负号. 轴下方的面积去负号. 三、例题解析: 例.求 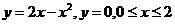 围成图形面积 围成图形面积解:1.分割 在区间 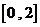 上等间隔地插入 上等间隔地插入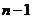 个点,将区间 个点,将区间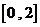 等分成 等分成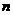 个小区间: 个小区间: 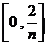 , ,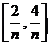 ,…, ,…,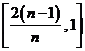 记第 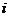 个区间为 个区间为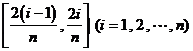 ,其长度为 ,其长度为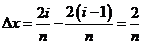 分别过上述 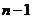 个分点作 个分点作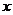 轴的垂线,从而得到 轴的垂线,从而得到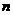 个小曲边梯形,他们的面积分别记作: 个小曲边梯形,他们的面积分别记作:
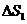 , , ,…, ,…,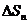 显然, 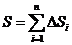 (2)近似代替 ∵ 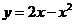 ,当 ,当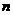 很大,即 很大,即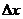 很小时,在区间 很小时,在区间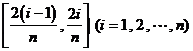 上,可以认为函数 上,可以认为函数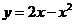 的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点 的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点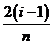 处的函数值 处的函数值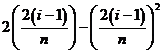 ,这样,在区间 ,这样,在区间 上,用小矩形的面积 上,用小矩形的面积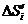 近似的代替 近似的代替 ,即在局部范围内“以直代取”,则有 ,即在局部范围内“以直代取”,则有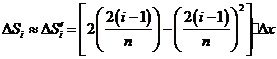 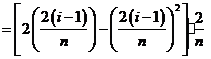 ① ①(3)求和 由①,上图中阴影部分的面积  为 为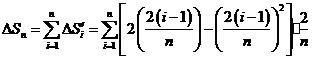 = 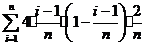 = =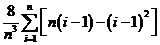 = 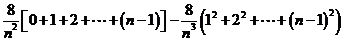 =  从而得到 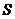 的近似值 的近似值 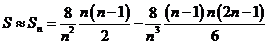 (4)取极限 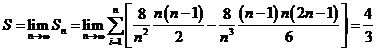 课堂巩固: 设S表示由曲线 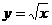 ,x=1,以及x轴所围成平面图形的面积,求S,并用定积分表示. ,x=1,以及x轴所围成平面图形的面积,求S,并用定积分表示.归纳反思: 合作探究: 1.计算由两条抛物线 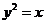 和 和 所围成的图形的面积 所围成的图形的面积2..计算 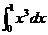 的值 的值 |
教师备课 学习笔记 教师备课 学习笔记 教师备课 学习笔记 教师备课 学习笔记 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com