
1. 向量有代数与几何两种形式,要理解两者的内在联系,善于从图形中发现向量间的关系。
(二).典例分析
例1:(1)设 与
与 为非零向量,下列命题:
为非零向量,下列命题:
①若 与
与 平行,则
平行,则 与
与 向量的方向相同或相反;
向量的方向相同或相反;
②若
 与
与 共线,则A、B、C、D四点必在一条直线上;
共线,则A、B、C、D四点必在一条直线上;
③若 与
与 共线,则
共线,则 ;④若
;④若 与
与 反向,则
反向,则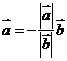
其中正确命题的个数有
(A)1个 (B)2个 (C)3个 (D)4个
(2)下列结论正确的是 ( )
(A)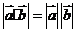 (B)
(B) (C)若
(C)若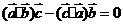
(D)若 与
与 都是非零向量,则
都是非零向量,则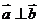 的充要条件为
的充要条件为
错解:(1)有学生认为①②③④全正确,答案为4;也有学生认为①或④是错的,答案为2或3;(2)A或B或C。
分析:学生对向量基础知识理解不正确、与实数有关性质运算相混淆,致使选择错误。
第(1)小题中,正确的应该是①④,答案为2。共线向量( 与
与 共线)的充要条件中所存在的常数
共线)的充要条件中所存在的常数 可看作为向量
可看作为向量 作伸缩变换成为另一个向量
作伸缩变换成为另一个向量 所作的伸缩量;若
所作的伸缩量;若 ,
, 为非零向量,则共线的
为非零向量,则共线的 与
与 满足
满足 与
与 同向时
同向时 ,
, 与
与 反向时
反向时 。
。
第(2)小题中,正确答案为(D)。学生的错误多为与实数运算相混淆所致。选择支D同时要求学生明确向量垂直、两个向量的数量积、向量的模之间互化方法,并进行正确互化。
例2 设a、b是两个不共线向量。AB=2a+kb BC=a+b CD=a-2b
A、B、D共线则k=_____(k∈R)
解:BD=BC+CD=a+b+a-2b=2a-b
2a+kb=λ(2a-b)=2λa-λb
∴ 2=2λ且 k=-λ
∴ k=-1
例3 梯形ABCD,且|AB|=2|DC|,M、N分别为DC、AB中点。
AB=a AD=b 用a,b来标DC、BC、MN。
解:DC=  AB=
AB= a
a
BC=BD+DC=(AD-AB)+DC =b-a+  a=b-
a=b-  a
a
MN=DN-DM= a-b-
a-b-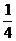 a=
a= 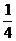 a-b
a-b
例4 |a|=10 b=(3,-4)且a∥b求a
解:设a=(x,y)则 x2+y2=100 (1)
由a∥b得 -4x-3y=0 (2)
解(1)(2)得 x=6 y=-8 。或 x=-6 y=8
∴ a=(6,-8)或(-6,8)
(一)基础知识训练
1.下列命题正确的是 ( )
 单位向量都相等
单位向量都相等  任一向量与它的相反向量不相等
任一向量与它的相反向量不相等
 平行向量不一定是共线向量
平行向量不一定是共线向量  模为
模为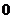 的向量与任意向量共线
的向量与任意向量共线
2. 已知正六边形 中,若
中,若
 ,
, 
 ,则
,则 ( )
( )



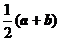

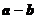


3. 已知向量
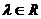 ,
,

 =2
=2 若向量
若向量 与
与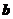 共线,则下列关系一定成立是 ( )
共线,则下列关系一定成立是 ( )

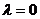

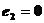

 ∥
∥

 ∥
∥ 或
或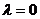
4. 若向量 ,
, 共线且方向相同,
共线且方向相同,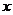 =__________。
=__________。
3.两个非零向量垂直的充要条件是
 ⊥
⊥ 

 ·
·  =0
=0
设  =(x1,y1),
=(x1,y1),
 =(x2,y2),则
=(x2,y2),则
 ⊥
⊥ 
 x1x2+y1y2=0
x1x2+y1y2=0
2.向量的基本运算
(1) 向量的加减运算
几何运算:向量的加减法按平行四边行法则或三角形法则进行。
坐标运算:设a =(x1,y1), b =(x2,y2)则a+b=(x1+x2,y1+y2 ) a-b=(x1-x2,y1-y2)
(2) 平面向量的数量积 : a b=
b=

 cos
cos
设a =(x1,y1),
b =(x2,y2)则a b=x1x2+y1y2
b=x1x2+y1y2
(3)两个向量平行的充要条件
 ∥
∥ 

 =λ
=λ 
若  =(x1,y1),
=(x1,y1),
 =(x2,y2),则
=(x2,y2),则
 ∥
∥ 
 x1y2-x2y1=0
x1y2-x2y1=0
1.向量的概念:
向量,零向量,单位向量,平行向量(共线向量),相等向量,向量的模等。
5、掌握平面向量的数量积及其几何意义。了解用平面向量的数量积可以处理有关长度,角度和垂直的问题,掌握向量垂直的条件。
4、了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算。
3、掌握实数与向量的积,理解两个向量共线的充要条件。
2、掌握向量的加法和减法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com