
1、正弦函数、余弦函数的图象和性质:(1)五点法作图:先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五点,再用光滑的曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象。常选取横坐标分别为0, 的五点。
的五点。
(2)正弦函数y=sinx是奇函数,对称中心是 ,对称轴是直线
,对称轴是直线 。
。
余弦函数y=cosx是偶函数,对称中心是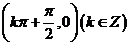 ,对称轴是直线
,对称轴是直线 。
。
练习:已知函数 为常数),且
为常数),且 ,则
,则 ______(答:-5);(3)函数
______(答:-5);(3)函数 的图象的对称中心和对称轴分别是__________、____________(答:
的图象的对称中心和对称轴分别是__________、____________(答: 、
、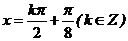 );(4)已知
);(4)已知 为偶函数,求
为偶函数,求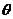 的值。(答:
的值。(答: )
)
(3)、单调性: 上单调递增,
上单调递增,
在 单调递减。
单调递减。
y=cosx在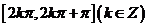 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。
如:函数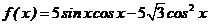
 的单调递增区间为___________(答:
的单调递增区间为___________(答: )
)
三角函数的单调性:正弦一,四增,二、三减。余弦三、四增,一、二减。正切只有增区间,余切只有减区间。强调象限的区间内。
13、万能公式: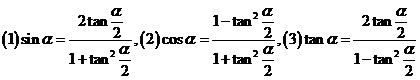

第十五讲三角函数的图象和性质
12、二倍角的正弦、余弦、正切
二倍角公式:
降幂公式与升幂公式: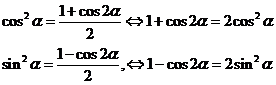
半角公式:
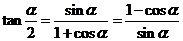
11、三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构。即首先观察角与角之间的关系,注意角的一些常用变式如:
巧变角:如 ,
, ,
, 等),
等),

如(1)已知 ,
, ,那么
,那么 的值是_____(答:
的值是_____(答: );(2)已知
);(2)已知 为锐角,
为锐角, ,
, ,则
,则 与
与 的函数关系为______(答:
的函数关系为______(答: ,注意:隐含y>0.
,注意:隐含y>0.
第二看函数名称之间的关系,通常“切化弦”第三观察代数式的结构特点。
10、化一公式:
如:(1)当函数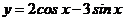 取得最大值时,
取得最大值时,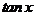 的值是______(答:
的值是______(答: );(2)如果
);(2)如果 是奇函数,则
是奇函数,则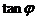 = (答:-2);
= (答:-2);
9、两角和公式:
 对第三式的
对第三式的
 的值使等式两边有意义。
的值使等式两边有意义。
注意公式的变形应用如: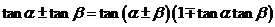

8、特殊角的三角函数值:(见下表)
|
|
30° |
45° |
60° |
0° |
90° |
180° |
270° |
15° |
75° |
|||||
sin |
 |
 |
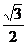 |
0 |
1 |
0 |
-1 |
 |
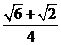 |
|||||
cos |
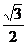 |
 |
 |
1 |
0 |
-1 |
0 |
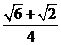 |
 |
|||||
tan |
 |
1 |
 |
0 |
|
0 |
|
2- |
2+ |
|||||
cot |
 |
1 |
 |
|
0 |
|
0 |
2+ |
2- |
|||||
7、同角三角函数的基本关系式:
平方关系:
倒数关系:sin csc
csc =1,cos
=1,cos sec
sec =1,tan
=1,tan cot
cot =1,
=1,
商数关系: ,一般采用“切化弦”,但已知一个角的正切值,求正弦与余弦有关的代数式常采用“弦化切”。
,一般采用“切化弦”,但已知一个角的正切值,求正弦与余弦有关的代数式常采用“弦化切”。
6、诱导公式:奇变偶不变,符号看象限。如:


熟记关系式:sin(kπ+α)=(-1)ksinα;cos(kπ+α)=(-1)kcosα(k∈Z).
 ;
;
5、象限角的三角函数符号:一全正,二正弦,三两切,四余弦。
根据三角函数线分析各象限的区间内各三角函数的单调性:正弦一,四增,二、三减。余弦三、四增,一、二减。正切只有增区间,余切只有减区间。强调象限的区间内。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com