
8、 柱坐标系与球坐标系:
如图在空间直角坐标系O-xyz内,设P产空间任意一点,它在Oxy平面上的射影为Q,用
 表示点Q在平面Oxy上的极坐标,这时P点的位置可用有序实数组
表示点Q在平面Oxy上的极坐标,这时P点的位置可用有序实数组 表示,这样建立了空间的点与有序实数组
表示,这样建立了空间的点与有序实数组 之间的一种对应关系。上述对应关系的坐标系叫柱坐标系,有序实数组
之间的一种对应关系。上述对应关系的坐标系叫柱坐标系,有序实数组 叫柱坐标。
叫柱坐标。
柱坐标系又称半极坐标系。
如图中设OP与Oz轴正方向的夹角为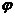 ,则P点的位置可用有序实数组
,则P点的位置可用有序实数组 表示,这种对应的坐标系叫球坐标系,
表示,这种对应的坐标系叫球坐标系, 叫球坐标。
叫球坐标。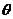 称被测点的方位角,
称被测点的方位角, 称为高低角。球坐标系又叫空间极坐标系。
称为高低角。球坐标系又叫空间极坐标系。

7、

利用圆锥曲线的极坐标方程可以简捷地解决与焦点弦、焦半径有关的问题。
6、几个特殊位置的圆的极坐标方程:
(1)当圆心位于极点: , (2)当圆心位于
, (2)当圆心位于 :
: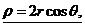 (3)当圆心位于
(3)当圆心位于 :
:
(4)若圆心为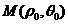 ,半径为r的圆方程为:
,半径为r的圆方程为:
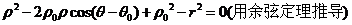
5.四类直线的极坐标方程:
(1)直线过极点且倾斜角为 :
:
(2)直线过点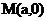 且垂直于极轴:
且垂直于极轴: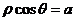
(3)直线过 且平行于极轴:
且平行于极轴:
(4)若直线过点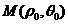 ,且极轴到此直线的角为
,且极轴到此直线的角为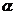 ,则它的方程为:
,则它的方程为:
4、. 极坐标与直角坐标的互化:
互化的前提条件:(1)极点与原点重合;(2)极轴与x轴正方向重合;(3)取相同的单位长度。 设点P的直角坐标为(x,y),它的极坐标为(r,q),则

若把直角坐标化为极坐标,求极角q时,应注意判断点P所在的象限(即角q的终边的位置),以便正确地求出角q。
利用两种坐标的互化,可以把不熟悉的问题转化为熟悉的问题。
3、 极坐标系: 极坐标系是用距离和角来表示平面上的点的位置的坐标系,它由极点O与极轴Ox组成。对于平面内任一点P,若设½OP½=r(³0),以Ox为始边,OP为终边的角为q,则点P可用有序数对(r,q)表示,(由于角q表示方法的多样性,故(r,q)的形式不唯一,即一个点的极坐标有多种表达形式)。对于极点O,其极坐标为(0,q),q为任意值,但一般取q=0,即极点的极坐标为(0,0)。
2、 平面直角坐标系中的伸缩变换:(1)

(2)将y=f(x)的横坐标变为原来的a倍,纵坐标变为原来的m倍,得到
即
(3)直线、双曲线、抛物线通过伸缩变换后仍分别为直线、双曲线、抛物线。但可以改变直线的倾斜角,双曲线的离心率、抛物线的开口大小及它们的位置。圆和椭圆可以通过伸缩变换进行转化。
1、 自觉运用坐标法解几何题
练习:(1)用坐标法证明三角形的三条高交于一点,(2)在已知三角形所在的平面内找一点,使它到各顶点的距离的平方和最小。
4、 两个分类变量x,y的独立性检验的依据是判断等式 是否成立。
是否成立。
了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用.
|
|
A |
 |
总计 |
|
B |
a |
b |
a+b |
 |
c |
d |
c+d |
|
总计 |
a+c |
b+d |
n=a+b+c+d |

第二十六讲坐标系与参数方程
3、回归分析中回归效果的判定:
①总偏差平方和: ②残差:
②残差: ;
;
③残差平方和:

残差点比较均匀地落在水平的带状区域中,说明选用的模型比较适合。带状区域越窄,模拟效果越好。如果某个样本点的残差特别大,那要考虑该数据的采集是否有误。
④相关指数

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com