
1、设函数 的定义域为[a,b],如果对于[a,b]内任意两数
的定义域为[a,b],如果对于[a,b]内任意两数 ,都有
,都有
 (1)
(1)
则称 为[a,b]上的凸函数。若把(1)式的不等号反向,则称这样的
为[a,b]上的凸函数。若把(1)式的不等号反向,则称这样的 为[a,b]上的凹函数。凸函数的几何意义是:过
为[a,b]上的凹函数。凸函数的几何意义是:过 曲线上任意两点作弦,则弦的中点必在该曲线的上方或在曲线上。
曲线上任意两点作弦,则弦的中点必在该曲线的上方或在曲线上。
②.基本不等式:  ≥
≥ (
( )
)
语言表述:n个正数的算术平均数不小于它们的几何平均数。
③.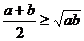 的几何解释:
的几何解释:
以 为直径作圆,在直径AB上取一点C,过C作弦DD’^AB 则
为直径作圆,在直径AB上取一点C,过C作弦DD’^AB 则 ,
,
 从而
从而 ,而半径
,而半径 。
。
一般地,设有两组实数: ,
, ,
, ,…,
,…, 与
与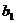 ,
, ,
, ,…,
,…,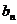 ,且它们满足:
,且它们满足:
 ≤
≤ ≤
≤ ≤…≤
≤…≤ ,
,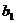 ≤
≤ ≤
≤ ≤…≤
≤…≤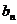 ,
,
若 ,
, ,
,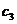 ,…,
,…, 是
是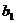 ,
, ,
, ,…,
,…,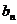 的任意一个排列,则和数
的任意一个排列,则和数 在
在 ,
, ,
, ,…,
,…, 与
与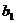 ,
, ,
, ,…,
,…,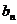 同序时最大,反序时最小,即:
同序时最大,反序时最小,即:
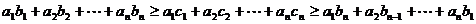 ,
,
等号当且仅当 或
或 时成立。
时成立。
4、定理4:(柯西不等式的推广形式):设 为大于1的自然数,
为大于1的自然数, (
(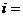 1,2,…,
1,2,…, )为任意实数,则:
)为任意实数,则: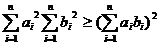 ,其中等号当且仅当
,其中等号当且仅当 时成立(当
时成立(当 时,约定
时,约定 ,
,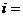 1,2,…,
1,2,…, )。
)。
证明:构造二次函数:
即构造了一个二次函数:
由于对任意实数 ,
, 恒成立,则其
恒成立,则其 ,
,
即: ,
,
即: ,
,
等号当且仅当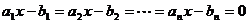 ,
,
即等号当且仅当 时成立(当
时成立(当 时,约定
时,约定 ,
,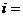 1,2,…,
1,2,…, )。如果
)。如果 (
( )全为0,结论显然成立。
)全为0,结论显然成立。
柯西不等式有两个很好的变式:
变式1 设
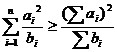 ,等号成立当且仅当
,等号成立当且仅当
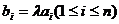
变式2 设ai,bi同号且不为0(i=1,2,…,n),则: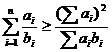 ,等号成立当且仅当
,等号成立当且仅当 。
。
3、定理3:(三角形不等式)设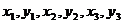 为任意实数,则:
为任意实数,则:

思考:三角形不等式中等号成立的条件是什么?
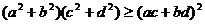 ,
,
其中等号当且仅当 时成立。
时成立。
几何意义:设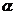 ,
, 为平面上以原点O为起点的两个非零向量,它们的终点分别为A(
为平面上以原点O为起点的两个非零向量,它们的终点分别为A( ),B(
),B( ),那么它们的数量积为
),那么它们的数量积为 ,
,
而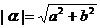 ,
,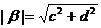 ,
,
所以柯西不等式的几何意义就是: ,
,
其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。
2、定理2:(柯西不等式的向量形式)设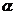 ,
, 为平面上的两个向量,则
为平面上的两个向量,则 ,其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。
,其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。
12. 常见曲线的参数方程的一般形式:
(1)经过点P0(x0,y0),倾斜角为a的直线的参数方程为
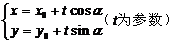 称为直线的标准参数方程。
称为直线的标准参数方程。

经过点P0(x0,y0),以 为方向向量的直线的参数方程为
为方向向量的直线的参数方程为
 称为直线的一般参数方程。
称为直线的一般参数方程。
此式中的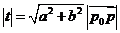 。
。
利用直线的参数方程,研究直线与圆锥曲线的位置关系以及弦长计算,有时比较方便。方法是:
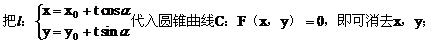
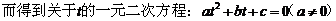
则(1)当△<0时,l与C无交点;(2)当△=0时,l与C有一公共点;(3)当△>0时,l与C有两个公共点;此时方程at2+bt+c=0有两个不同的实根t1、t2,把参数t1、t2代入l的参数方程,即可求得l与C的两个交点M1、M2的坐标;另外,由参数t的几何

(2) 圆、椭圆、双曲线、抛物线的参数方程




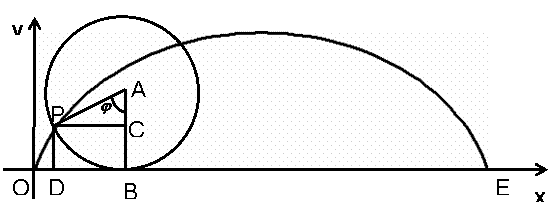
(3)摆线:
当一个圆沿着一条定直线无滑动地滚动时,圆周上一个定点P的轨迹是什么?
我们把定点P的轨迹叫做平摆线,又叫旋轮线。

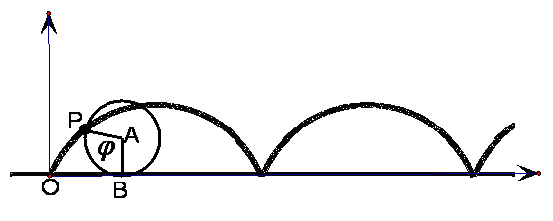
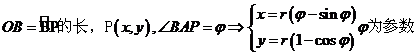
(4)圆的渐开线:


第二七讲不等式选讲
11、 化普通方程为参数方程的基本思路是引入参数,即选定合适的参数t,先确定一个关系x=f(t)(或y=j(t)),再代入普通方程F(x,y)=0,求得另一关系y=j(t)(或x=f(t))。一般地,常选择的参数有角(如圆、椭圆、双曲线)、有向线段的数量(如直线)、斜率(抛物线是以斜率的倒数为参数),某一点的横坐标(或纵坐标)。
10、 化参数方程为普通方程的基本思路是消去参数,常用的消参方法有代入消去法、加减消去法、恒等式(三角的或代数的)消去法。要注意整体代入法及参数的取值范围对x,y的取值范围的影响。
9、参数方程与普通方程的区别与联系:
在求曲线的方程时,一般地需要建立曲线上动点P(x,y)的坐标x,y之间满足的等量关系F(x,y)=0,这样得到的方程F(x,y)=0就是曲线的普通方程;而有时要想得到联系x,y的方程F(x,y)=0是比较困难的,于是可以通过引入某个中间变量t,使之与曲线上动点P的坐标x,y间接地联系起来,此时可得到方程组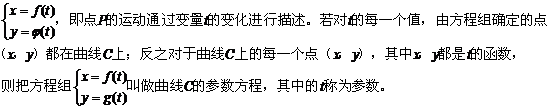
显然,参数方程与普通方程的最明显的区别是其方程形式上的区别,更大的区别是普通方程反映了曲线上任一点坐标x,y的直接关系,而参数方程则反映了x,y的间接关系。
尽管参数方程与普通方程有很大的区别,但他们之间又有着密切的联系,这种联系表现在两方面:(1)这两种方程都是同一曲线的不同的代数表现形式,是同一事物的两个方面;(2)这两种方程之间可以进行互化,通过消参可以把参数方程化为普通方程,而通过引入参数,也可把普通方程化为参数方程。需要注意的是,在将两种方程互化的过程中,要注意两种方程(在表示同一曲线的)等价性,即注意参数的取值范围对x,y的取值范围的影响。
实质上,参数的思想方法就是在运动变化的哲学思想指导下的函数的思想方法,因此也可认为引入参数就是引入函数的自变量。参数法在求曲线的轨迹方程,以及研究某些最值问题时是一种常用的甚至是简捷的解题方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com