
2.教材课本习题14.5第3题

 应用举例(四)
应用举例(四)
1.如图6-28,在等腰梯形ABCD中,DC∥AB, DE⊥AB于E,
AB=8, DE=4, cosA=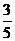 , 求CD的长.
, 求CD的长.
(三)小结
请学生作小结,教师补充.
本节课教学内容仍是解直角三角形,但问题已是处理一些实际应用题,在这些问题中,有较多的专业术语,关键是要分清每一术语是指哪个元素,再看是否放在同一直角三角形中,这时要灵活,必要时还要作辅助线,再把问题放在直角三角形中解决.在用三角函数时,要正确判断边角关系.

(二)重点、难点的学习与目标完成过程
1.出示已准备的泥燕尾槽,让学生有感视印象,将其横向垂直于燕尾槽的平面切割,得横截面,请学生通过观察,认识到这是一个等腰梯形,并结合图形,向学生介绍一些专用术语,使学生知道,图中燕尾角对应哪一个角,外口、内口和深度对应哪一条线段.这一介绍,使学生对本节课内容很感兴趣,激发了学生的学习热情.
2.例题
例 燕尾槽的横断面是等腰梯形,图6-26是一燕尾槽的横断面,其中燕尾角B是55°,外口宽AD是180mm,燕尾槽的深度是70mm,求它的里口宽BC(精确到1mm).
分析:(1)引导学生将上述问题转化为数学问题;等腰梯形ABCD中,上底AD=180mm,高AE=70mm,∠B=55°,求下底BC.

(2)让学生展开讨论,因为上节课通过做等腰三角形的高把其分割为直角三角形,从而利用解直角三角形的知识来求解.学生对这一转化有所了解.因此,学生经互相讨论,完全可以解决这一问题.
解:作AE DF
DF 那么在Rt△ABE中.
cotB=
那么在Rt△ABE中.
cotB= ,
,
∴BE=AE·cotB
=70×0.7002
≈49.0(mm).
∴BC=2BE+AD
≈2×49.0+180
=278(mm).
答:燕尾槽的里口宽BC约为278mm.
例题小结:遇到有关等腰梯形的问题,应考虑如何添加辅助线,将其转化为直角三角形和矩形的组合图形,从而把求等腰梯形的下底的问题转化成解直角三角形的问题.
3.巩固练习
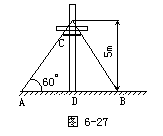
如图6-27,在离地面高度5米处引拉线固定电线杆,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD(精确到0.01米).
分析:(1)请学生审题:因为电线杆与地面应是垂直的,那么图6-27中△ACD是直角三角形.其中CD=5m,∠CAD=60°,求AD、AC的长.
(2)学生运用已有知识独立解决此题.教师巡视之后讲评.
解:∵CD⊥AB,
那么在Rt△ACD中,
sin ,
,

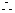 AC=
AC=
又

答:拉线AC的长是5.77m,拉线下端点A与杆底D的距离AD是2.89m.
(一)明确目标
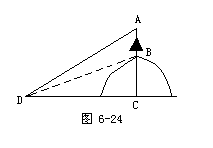
如图6-25,Rt△ABC中,∠C为Rt∠,若已知∠A及a,求b.

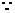 cotA=
cotA=
∴b=a·cotA.
此图恰是燕尾槽中被分割出来的Rt△,课前抛出这一问题为解例题做铺垫.
2.难点:如何添作适当的辅助线.
1.重点:把等腰梯形转化为解直角三角形问题;
(三)德育渗透点
培养学生用数学的意识;渗透转化思想;渗透数学来源于实践又作用于实践的观点.
(一)知识教学点
使学生懂得什么是横断面图,能把一些较复杂的图形转化为解直角三角形的问题.
3.在宽为30米的街道东西两旁各有一楼房,从东楼底望西楼顶仰角为45°,从西楼顶望东楼顶,俯角为10°,求西楼高(精确到0.1米).
应用举例(三)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com