
22. Let’s go to cinema-that’ll take your mind off the problem for while
A. the; the B. the; a
C. a; the D. a ; a
第一节 单项填空(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
例: We last night, but we went to the concert instead.
A. must have studied B. might study
C. should have studied D. would study
答案是C
21. -It looks heavy. Can I give you a hand?
- .
A. No, thanks B. Yes, my pleasure
C. No, never mind D. Yes, I do
例1(05辽宁、理12)一给定函数 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意 ,由关系式
,由关系式 得到的数列
得到的数列 满足
满足 ,则该函数的图象是
( )
,则该函数的图象是
( )
A B C D
解析:∵
则若 ;
;
根据函数与不等式之间的关系得,
 的函数图像应在
的函数图像应在 的上方
的上方
∴答案为A
评注:这道题目,是当年辽宁卷的压轴选择题;大多数学生感到无从下手,没有抓住问题的实质;结果弄错了答案,丢了分。如果解题时,你感到题目特别难、无从下手时,是不是要用特例法了。切记,切记!
特例法在高考中考的并不多,一旦考上,往往是大多数学生失分的题目;高考不但考知识、能力,还考你对数学思想的理解和应用程度;一般与特殊的思想是高考考纲要求的数学思想,同学们应掌握这种数学思想的解题技巧,并会灵活应用它。
张掖市实验中学 734300 13119368515 750207wxh@
自我简介 王新宏 男 98年毕业于西北师范大学数学系数学教育专业。从03年起,连续带高三七年
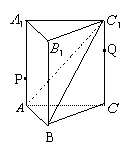
例1(05全国Ⅲ、理4)4、设三棱柱 的体积为
的体积为 ,
, 分别是侧棱
分别是侧棱 、
、 上的点,且
上的点,且 ,则四棱锥
,则四棱锥 的体积为( )
的体积为( )
 A
A  B
B  C
C  D
D 
解析:不妨取正三棱锥且满足 ,
,
不妨取 =0;
=0;
此时
评注:满足题意的点P和Q有无穷多个,特殊位置也不止一个;比如P和Q都取中点,也能得到答案;但过程较繁。取 =0,使得P与A重合;Q与
=0,使得P与A重合;Q与  重合,特例推到极限情形,问题就相当简单了。故特例只要满足题意,越简单越好。
重合,特例推到极限情形,问题就相当简单了。故特例只要满足题意,越简单越好。
例2(08全国Ⅱ、理12)已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )
 A.1 B.
A.1 B. C.
C.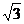 D.2
D.2
解析:如右图,不妨设其中一个面过球心,
则圆心距=
评注:高考题不怕你做不到,就怕你想不到。
例1(07安徽、文11)定义在 上的函数
上的函数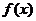 既是奇函数,又是周期函数,
既是奇函数,又是周期函数, 是它的一个正周期.若将方程
是它的一个正周期.若将方程 在闭区间
在闭区间 上的根的个数记为
上的根的个数记为 ,则
,则 可能为( )
可能为( )
A.0 B.1 C.3 D.5
解析:联想满足题设的函数,我们取 则答案为D。
则答案为D。
评注:千万别担心,你的特例太简单了,会把题做错。只要满足题意,越简单越好。
例2(06辽宁,理2) 设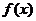 是R上的任意函数,则下列叙述正确的是
是R上的任意函数,则下列叙述正确的是
(A) 是奇函数 (B)
是奇函数 (B) 是奇函数
是奇函数
(C) 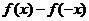 是偶函数 (D)
是偶函数 (D)  是偶函数
是偶函数
解析:取 ,排除A、C.再取
,排除A、C.再取 ,排除B;故选择答案D。
,排除B;故选择答案D。
评注:取特例取我们最熟悉的,这样有利于解题。
例3(07江西、理11)设函数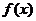 是
是 上以5为周期的可导偶函数,则曲线
上以5为周期的可导偶函数,则曲线 在
在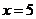 处的切线的斜率为( )
处的切线的斜率为( )
A. B.
B. C.
C. D.
D.
解析:联想满足题设的函数,我们取 则答案为B
则答案为B
评注:以5为周期的可导偶函数,你不得不想到三角函数
例4(04全国Ⅳ、理12)设函数 为奇函数,
为奇函数,
 则
则 (
)
(
)
A.0 B.1 C. D.5
D.5
解析:根据题意,联系我们学过的所有函数。只有一次函数 满足
满足
题设∴ ,得
,得 ;∴
;∴ ;得
;得 ;故选C
;故选C
评注:很多抽象函数都以我们学过的函数为模型,同学们可以认真体会与总结。
例5(06江西、理5)对于R上可导的任意函数f(x),若满足(x-1)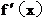 ³0,则必有(
)
³0,则必有(
)
A. f(0)+f(2)<2f(1) B. f(0)+f(2)£2f(1)
C. f(0)+f(2)³2f(1) D. f(0)+f(2)>2f(1)
解析:依题意,当x³1时,f¢(x)³0,函数f(x)在(1,+¥)上是增函数;当x<1时,f¢(x)£0,f(x)在(-¥,1)上是减函数,故f(x)当x=1时取得最小值,联想我们学过的函数,取 ,排除A,B;再想若
,排除A,B;再想若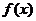 为常值函数也满足题意;故选C
为常值函数也满足题意;故选C
评注:当取一个特例不能排除所有的错误项,且剩余项还十分相近时,应全面考虑;做到不重复也不遗漏。
例1(05全国Ⅱ、理7)如果数列 是等差数列,则( )
是等差数列,则( )
(A) +
+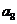 <
< +
+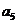 (B)
(B) +
+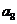 =
= +
+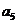
(C) +
+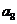
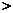
 +
+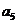 (D)
(D)
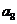 =
=
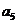
解析:取 ,得答案为B
,得答案为B
例1(08天津卷、理3)函数 (
( )的反函数是( )
)的反函数是( )
(A) (
(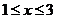 ) (B)
) (B) (
( )
)
(C) (
(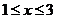 ) (D)
) (D) (
( )
)
解析:原函数经过(4,3)点,它的反函数经过(3,4)点;排除C,D;再根据原函数是增函数,得值域为 ,故反函数的定义域为
,故反函数的定义域为 ;选A
;选A
评注:最快最简单的方法就是最好的方法。
 例2(07全国Ⅱ、理12)设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点,若
例2(07全国Ⅱ、理12)设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点,若 ,则|FA|+|FB|+|FC|=( )
,则|FA|+|FB|+|FC|=( )
(A)9 (B) 6 (C) 4 (D) 3
解析: ,不妨取A(0,0)
,不妨取A(0,0)
 则
则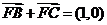 ,即
,即 =1;做平行四边形FCDB
=1;做平行四边形FCDB
 ∵抛物线关于x轴对称
∵抛物线关于x轴对称
|
∴FD⊥BC,即B,C两点的横坐标均为 ;得
;得
∴|FA|+|FB|+|FC|=1+5=6;故选B
评注:此题若分析出点F为△ABC的重心,则解法就更简单了。若分析不出, 此法也不错。
此法也不错。
 例1(06四川,理4).如图, 已知正六边形
例1(06四川,理4).如图, 已知正六边形 ,下列向量的数量积中最大的是( )
,下列向量的数量积中最大的是( )
(A) (B)
(B)
(C) (D)
(D)
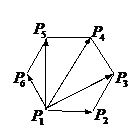
 解析:如图:不妨设正六边形
解析:如图:不妨设正六边形 边长为1,
边长为1,
根据正六边形的性质,得答案为A
评注:特例越简单越好,越方便越好。
例2(06全国Ⅰ,理9)、设平面向量 、
、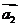 、
、 的和
的和 。如果向量
。如果向量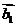 、
、 、
、 ,满足
,满足 ,且
,且 顺时针旋转
顺时针旋转 后与
后与 同向,其中
同向,其中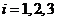 ,则( )
,则( )
A. B.
B.
C. D.
D.
解析:∵ ,∴不妨取
,∴不妨取 ,且
,且 起点在原点,在
起点在原点,在 轴正半轴上;则向量
轴正半轴上;则向量 、
、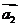 、
、 顺时针旋转
顺时针旋转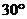 后与
后与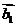 、
、 、
、 同向,且
同向,且 =2,∴
=2,∴ ,选D.
,选D.
评注:一般问题特殊化,不会失去一般性。
例1(07安徽、文8)设 ,且
,且 ,
, ,
,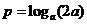 ,则
,则 的大小关系为( )
的大小关系为( )
A. B.
B. C.
C. D.
D.
解析:取a=2,得答案B
评注:所选取的特例要符合题设条件,且越简单越好。
例2(07江西、理5)若 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A. B.
B.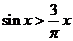
C.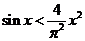 D.
D.
解析:取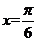 ,排除A,B,C,得D
,排除A,B,C,得D
评注:一般情况下,特例法与排除法结合起来使用。
例3(06安徽、理11)如果 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于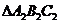 的三个内角的正弦值,则
( )
的三个内角的正弦值,则
( )
A. 和
和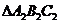 都是锐角三角形
都是锐角三角形
B. 和
和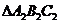 都是钝角三角形
都是钝角三角形
C. 是钝角三角形,
是钝角三角形,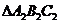 是锐角三角形
是锐角三角形
D. 是锐角三角形,
是锐角三角形,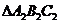 是钝角三角形
是钝角三角形
解析: 三角形中角的正弦值均为正
三角形中角的正弦值均为正
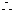
 的三内角的余弦值也为正
的三内角的余弦值也为正
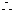
 是锐角三角形
是锐角三角形
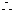 取
取
得 所以选D
所以选D
评注:所取的特例必须是我们非常熟悉的,越简单越好。
例4(06辽宁,理10) 直线 与曲线
与曲线
 的公共点的个数为( )
的公共点的个数为( )
(A)1 (B)2 (C)3 (D)4
解析:不妨取k=1,将 代入
代入 得:
得:
 ,显然该关于
,显然该关于 的方程有两正解,即
的方程有两正解,即 有四解,
有四解,
所以交点有4个,故选择答案D。
评注:任意不等于0的k都满足,k取1当然满足;不要担心做错题。
例5(06陕西,理10)已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2,x1+x2=1-a,则( )
A.f(x1)<f(x2) B.f(x1)=f(x2)
C.f(x1)>f(x2) D.f(x1)与f(x2)的大小不能确定
解析:取a=1得函数f(x)=x2+2x+4,二次函数的图象开口向上,对称轴为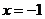 ,∴ x1+x2=0,∴ x2到对称轴的距离大于x1到对称轴的距离。
,∴ x1+x2=0,∴ x2到对称轴的距离大于x1到对称轴的距离。
∴ f(x1)<f(x2) ,选A.
评注:0<a<3中的任何一个值都满足题设,a=1也满足。
例6(06湖南,理2). 若数列 满足:
满足:  , 且对任意正整数
, 且对任意正整数 都有
都有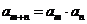 ,则
,则 ( )
( )
A. B.
B. C.
C. D.
D.
解析:数列 满足:
满足:  , 且对任意正整数
, 且对任意正整数 都有
都有 ;所以
;所以 ,
,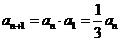 ,∴数列
,∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列。
的等比数列。
 ,选A.
,选A.
评注:任意正整数 都有
都有 ,取m=1又未尝不可。
,取m=1又未尝不可。
2009中考英语部分的听力试题总分为30分,占总分150分的20%。题型分为以下四大部分:
1. 听句子选图画,6分
由于听到的是六句句子,而看到的是七幅图,所以首先要看清图片的内容,然后再听清每句句子中关键词,最后进行筛选。而今年来,图片题中越来越涉及一些文化常识的了解。比如法国在图片中会以埃菲尔铁塔的形式出现,圣诞节会以圣诞树的形式出现。
所以在2009年的图片题中,考生应该特别注意一些文化常识方面的知识储备。
2. 听对话回答问题,10分
对话题每年考点中的重点题型,在2009年的中考应该还是会有所体现。比如建议考点,逻辑考点,数字考点,比较考点,这些都是历年经常出现在试题中的考点,对于这些考点的把握,考生应该结合上课笔记,做到熟识关键词,表达方式和及时笔记记录。
3. 听短文判断句子正误,7分
语段上来说,短文的理解上应该是相较来说比较难的,但是每年的题目本身难度上要求不高,再加上答案选择只有T,F两种,每篇文章又有听两次的机会,所以要求上并不高。针对这样的题型,还是主抓细节。因为7道题目里,基本5题都是细节题,只有2题会涉及到理解判断层面。所以应该好好把握听两遍的机会,体会题干句子细节与听力原文中的细微差别,也要能自己总结出短文的主导观念,再结合一些关键词的把握,用这样的思路解题,会事半功倍。
4. 听录音填写对话或表格,7分
这是2009年中考英语听力中改革的一部分,和以往的“听对话填写表格”不同,本次考试会以直接给出段落文字,代替表格的形式表现。从听力理解的难度上来说,应该降低了,但是对于考生的一些硬性要求还是没降低。比如单词要过关,特别是一些特殊的人名、国名、国籍、职业、学科、兴趣爱好、活动、活动时间、活动地点等,对同学们的单词拼写要求是相当高的;除此之外保持填入单词的语法正确,也是很重要的另一方面,如名词单复数、动词第三人称单数在一般现在时中加S,过去式与过去分词的选用,大小写的选用等等。除此之外,作为唯一的主观题,还要注意卷面书写的规范和整洁。
“中考”已经迫在眉睫,每个考生都应当在各个方面作好考试的准备。希望以上的文字和建议能对大家,在最后2个月的中考英语复习上提供一些参考和帮助,祝愿每个考生都能马到成功!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com