
4.从 点出发的三条射线两两垂直,空间一点
点出发的三条射线两两垂直,空间一点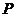 到这三条射线的距离分别为
到这三条射线的距离分别为 ,则
,则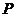 到
到 的距离为
的距离为 .
.
3.已知 ,
, ,其中
,其中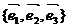 是一组正交基底,
是一组正交基底, 及
及 之间的夹角的余弦值为
之间的夹角的余弦值为 .
.
2.已知 ,且点
,且点 、
、 、
、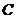 、
、 不共线,则下列结论正确的是
(
不共线,则下列结论正确的是
(  )
)
 四边形
四边形 是平行四边形
是平行四边形  四边形
四边形 是平行四边形
是平行四边形
 四边形
四边形 是梯形
是梯形  四边形
四边形 是梯形
是梯形
1.四面体 中,SC=AB=1,
中,SC=AB=1, 与
与 中点分别为
中点分别为 ,且
,且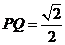 ,则异面直线
,则异面直线 与
与 所成的角为
所成的角为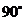 .
.
例1.在平行四边形 中,
中, ,
, ,将它沿对角线
,将它沿对角线 折起,使
折起,使 与
与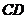 成
成 角,求
角,求 、
、 间的距离.(答案:
间的距离.(答案: )
)
 例2.在矩形
例2.在矩形 中,已知
中,已知 ,
, ,
, 平面
平面 ,
, ,若
,若 边上存在唯一一点
边上存在唯一一点 ,使得
,使得 ,
, 是
是 上一点,
上一点, 在平面
在平面 上的射影恰好是
上的射影恰好是 的重心,求线段
的重心,求线段 的长度及
的长度及 到平面
到平面 的距离.(答案:
的距离.(答案: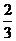 )
)
例3.在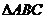 中
中 ,现将
,现将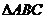 沿着平面
沿着平面 的法向量
的法向量 平移到
平移到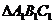 的位置,
的位置,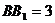 ,
, 是
是 的中点,
的中点,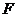 是
是 的中点,
的中点, 在
在 上,
上,
 ⑴当
⑴当 时,求直线
时,求直线 与
与 所成角的大小;
所成角的大小;
⑵当 点在
点在 上变化时,
上变化时, 为多长时
为多长时 .
.
答案:⑴ ;⑵
;⑵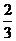 .
.
7.已知向量 ,
, ,则向量
,则向量 在向量
在向量 方向上的射影向量的模为
方向上的射影向量的模为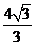 .
.
6.已知 是空间二向量,若
是空间二向量,若 ,则
,则 与
与 的夹角为
的夹角为 .
.
5.已知 ,
,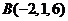 ,
, ,若
,若 且
且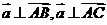 ,则
,则 的坐标为
的坐标为  .
.
4.若 ,
,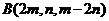 ,
, 三点共线,则
三点共线,则 =
= .
.
3.O是平面上一定点,A、B、C是平面上不共线的三个点,动点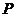 满足
满足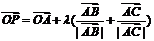 ,
, ,则
,则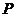 的轨迹一定通过
的轨迹一定通过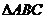 的 (
的 (
 )
)
 外心
外心  内心
内心  重心
重心  垂心
垂心
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com