
10..图是一个几何体的三视图,若它的体积是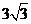 ,则a=_______
,则a=_______
答案 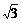
8.若正方体的棱长为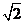 ,则以该正方体各个面的中心为顶点的凸多面体的体积为
,则以该正方体各个面的中心为顶点的凸多面体的体积为
A.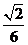 B.
B. C.
C.  D.
D.
答案 C
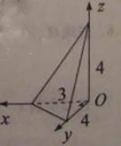
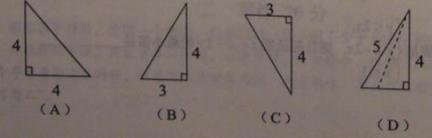 9,如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的主视图是( )
9,如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的主视图是( )
答案 B
7. 如图,在半径为3的球面上有
如图,在半径为3的球面上有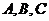 三点,
三点,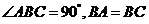 ,
,
球心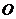 到平面
到平面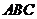 的距离是
的距离是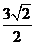 ,则
,则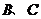 两点的球面距离是
两点的球面距离是
A.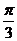 B.
B. C.
C.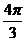 D.
D.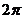


答案 B
6.纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北。现有沿该正方体
的一些棱将正方体剪开、外面朝上展平,得到右侧的平面图形,则标“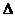 ”的面的方位是
”的面的方位是
A. 南 B. 北
C. 西 D. 下
解:展、折问题。易判断选B
5. 如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为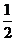 。则该集合体的俯视图可以是
。则该集合体的俯视图可以是
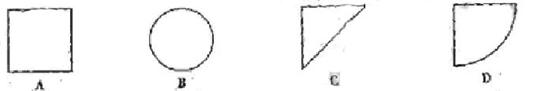
答案: C
4.在区间[-1,1]上随机取一个数x,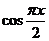 的值介于0到
的值介于0到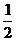 之间的概率为( ).
之间的概率为( ).
A.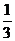 B.
B. C.
C.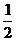 D.
D.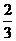
[解析]:在区间[-1,1]上随机取一个数x,即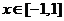 时,
时,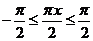 ,
∴
,
∴
区间长度为1, 而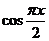 的值介于0到
的值介于0到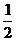 之间的区间长度为
之间的区间长度为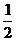 ,所以概率为
,所以概率为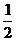 .故选C
.故选C
答案 C
[命题立意]:本题考查了三角函数的值域和几何概型问题,由自变量x的取值范围,得到函数值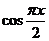 的范围,再由长度型几何概型求得.
的范围,再由长度型几何概型求得.
3.正六棱锥P-ABCDEF中,G为PB的中点,则三棱锥D-GAC与三棱锥P-GAC体积之比为
(A)1:1 (B) 1:2 (C) 2:1 (D) 3:2
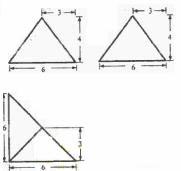
2.一个棱锥的三视图如图,则该棱锥的全面积(单位:c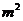 )为
)为
(A)48+12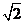 (B)48+24
(B)48+24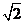 (C)36+12
(C)36+12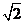 (D)36+24
(D)36+24
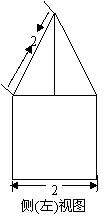
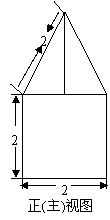
1. 一空间几何体的三视图如图所示,则该几何体的体积为( ).
 A.
A. B.
B. 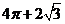 C.
C.
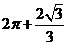 D.
D.
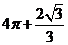
[解析]:该空间几何体为一圆柱和一四棱锥组成的,
 圆柱的底面半径为1,高为2,体积为
圆柱的底面半径为1,高为2,体积为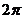 ,四棱锥的底面
,四棱锥的底面
边长为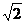 ,高为
,高为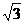 ,
,
所以体积为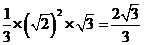
所以该几何体的体积为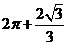 .
.
答案:C
[命题立意]:本题考查了立体几何中的空间想象能力,
由三视图能够想象得到空间的立体图,并能准确地
计算出.几何体的体积.
2009年高考题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com