13、直线和平面所成的角：(1)定义：平面的一条斜线和它在平面内的射影所成的锐角，叫这条直线和这个平面所成的角。(2)范围：；(3)求法：作出直线在平面上的射影；(4)斜线与平面所成的角的特征：斜线与平面中所有直线所成角中最小的角。如(1)在正三棱柱ABC-A₁B₁C₁中，已知AB=1，D在棱BB₁上，BD=1，则AD与平面AA₁C₁C所成的角为______(答：arcsin)；(2)正方体ABCD-A₁B₁C₁D₁中，E、F分别是AB、C₁D₁的中点，则棱 A₁B₁ 与截面A₁ECF所成的角的余弦值是______(答：)；(3)是从点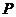引出的三条射线，每两条的夹角都是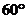，则直线与平面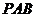所成角的余弦值为______(答：)；(4)若一平面与正方体的十二条棱所在直线都成相等的角θ，则sinθ的值为______(答：)。

12、三垂线定理及逆定理：(1)定理：在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。(2)逆定理：在平面内的一条直线，如果它和这个平面的一条斜线，那么它也和这条斜线在平面内的射影垂直。其作用是证两直线异面垂直和作二面角的平面角。

11、直线和平面垂直的判定和性质：(1)判定：①如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线和这个平面垂直。②两条平行线中有一条直线和一个平面垂直，那么另一条直线也和这个平面垂直。(2)性质：①如果一条直线和一个平面垂直，那么这条直线和这个平面内所有直线都垂直。②如果两条直线都垂直于同一个平面，那么这两条直线平行。如(1)如果命题“若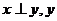∥z，则”不成立，那么字母x、y、z在空间所表示的几何图形一定是_____(答：x、y是直线，z是平面)；(2)已知a，b，c是直线，α、β是平面，下列条件中能得出直线a⊥平面α的是　 A、a⊥b，a⊥c其中bα，cα　B、a⊥b ，b∥α　C、α⊥β，a∥β　 D、a∥b，b⊥α(答：D)；(3)AB为⊙O的直径，C为⊙O上的一点，AD⊥面ABC，AE⊥BD于E，AF⊥CD于F，求证：BD⊥平面AEF。

10、直线与平面平行的判定和性质：(1)判定：①判定定理：如果平面内一条直线和这个平面平面平行，那么这条直线和这个平面平行；②面面平行的性质：若两个平面平行，则其中一个平面内的任何直线与另一个平面平行。(2)性质：如果一条直线和一个平面平行，那么经过这条直线的平面和这个平面相交的交线和这条直线平行。在遇到线面平行时，常需作出过已知直线且与已知平面相交的辅助平面，以便运用线面平行的性质。如(1)α、β表示平面，a、b表示直线，则a∥α的一个充分不必要条件是　A、α⊥β，a⊥β　　　B、α∩β＝b，且a∥b　C、a∥b且b∥α　D、α∥β且aβ(答：D)；(2)正方体ABCD-A₁B₁C₁D₁中，点N在BD上，点M在B₁C上，且CM=DN，求证：MN∥面AA₁B₁B。

9、直线与平面的位置关系：(1)直线在平面内；(2)直线与平面相交。其中，如果一条直线和平面内任何一条直线都垂直，那么这条直线和这个平面垂直。注意：任一条直线并不等同于无数条直线；(3)直线与平面平行。其中直线与平面相交、直线与平面平行都叫作直线在平面外。如(1)下列命题中，正确的是 A、若直线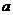平行于平面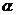内的一条直线b , 则 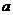// 　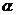B、若直线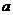垂直于平面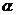的斜线b在平面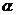内的射影，则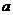⊥b　C、若直线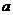垂直于平面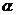,直线b是平面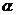的斜线，则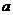与b是异面直线　D、若一个棱锥的所有侧棱与底面所成的角都相等，且所有侧面与底面所成的角也相等，则它一定是正棱锥(答：D)；(2)正方体ABCD-A₁B₁C₁D₁中，点P在侧面BCC₁B₁及其边界上运动，并且总保持AP⊥BD₁，则动点P的轨迹是___________(答：线段B₁C)。

8、两直线垂直的判定：(1)转化为证线面垂直；(2)三垂线定理及逆定理。

7、两直线平行的判定：(1)公理4：平行于同一直线的两直线互相平行；(2)线面平行的性质：如果一条直线和一个平面平行，那么经过这条直线的平面和这个平面相交的交线和这条直线平行；(3)面面平行的性质：如果两个平行平面同时与第三个平面相交，那么它们的交线平行；(4)线面垂直的性质：如果两条直线都垂直于同一个平面，那么这两条直线平行。

6、异面直线的距离的概念：和两条异面直线都垂直相交的直线叫异面直线的公垂线。两条异面直线的公垂线有且只有一条。而和两条异面直线都垂直的直线有无数条，因为空间中，垂直不一定相交。如(1)ABCD是矩形，沿对角线AC把ΔADC折起，使AD⊥BC，求证：BD是异面直线AD与BC的公垂线；(2)如图，在正方体ABCD-A₁B₁C₁D₁中，EF是异面直线AC与A₁D的公垂线，则由正方体的八个顶点所连接的直线中，与EF平行的直线有____条(答：1)；

5、异面直线所成角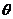的求法：(1)范围：；(2)求法：计算异面直线所成角的关键是平移(中点平移，顶点平移以及补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，以便易于发现两条异面直线间的关系)转化为相交两直线的夹角。如(1)正四棱锥的所有棱长相等，是的中点，那么异面直线与所成的角的余弦值等于____(答：)；(2)在正方体AC₁中，M是侧棱DD₁的中点，O是底面ABCD的中心，P是棱A₁B₁上的一点，则OP与AM所成的角的大小为____(答：90°)；(3)已知异面直线a、b所成的角为50°，P为空间一点，则过P且与a、b所成的角都是30°的直线有且仅有____条(答：2)；(4)若异面直线所成的角为，且直线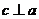，则异面直线所成角的范围是____(答：)；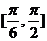

4、异面直线的判定：反证法。 如(1)“a、b为异面直线”是指：①a∩b＝Φ，但a不平行于b；②a面α，b面β且a∩b＝Φ；③a面α，b面β且α∩β＝Φ；④a面α，b面α　；⑤不存在平面α，能使a面α且b面α成立。上述结论中，正确的是_____(答：①⑤)；(2)在空间四边形ABCD中，M、N分别是AB、CD的中点，设BC+AD=2a，则MN与a的大小关系是_____(答：MN<a)；(3)若E、F、G、H顺次为空间四边形ABCD四条边AB、BC、CD、DA的中点，且EG=3，FH=4，则AC²+BD²= 　　　　　　_____(答：50)；(4)如果a、b是异面直线，P是不在a、b上的任意一点，下列四个结论：①过点P一定可以作直线与a、b都相交；　②过点P一定可以作直线与a、b都垂直；③过点P一定可以作平面α与a、b都平行；　④过点P一定可以作直线与a、b都平行。其中正确的结论是_____(答：②)；(5)如果两条异面直线称作一对，那么正方体的十二条棱中异面直线的对数为_____(答：24)；(6)已知平面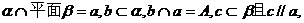求证：b、c是异面直线．