
3. 同一函数的概念。构成函数的三要素是定义域,值域和对应法则。而值域可由定义域和对应法则唯一确定,因此当两个函数的定义域和对应法则相同时,它们一定为同一函数。如若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“天一函数”,那么解析式为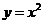 ,值域为{4,1}的“天一函数”共有______个(答:9)
,值域为{4,1}的“天一函数”共有______个(答:9)
2.函数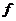 : A
: A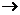 B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与
B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与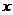 轴的垂线至多有一个公共点,但与
轴的垂线至多有一个公共点,但与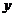 轴垂线的公共点可能没有,也可能有任意个。如(1)已知函数
轴垂线的公共点可能没有,也可能有任意个。如(1)已知函数 ,
,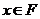 ,那么集合
,那么集合 中所含元素的个数有 个(答: 0或1);(2)若函数
中所含元素的个数有 个(答: 0或1);(2)若函数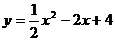 的定义域、值域都是闭区间
的定义域、值域都是闭区间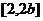 ,则
,则 = (答:2)
= (答:2)
1.映射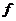 : A
: A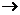 B的概念。在理解映射概念时要注意:⑴A中元素必须都有象且唯一;⑵B中元素不一定都有原象,但原象不一定唯一。如(1)设
B的概念。在理解映射概念时要注意:⑴A中元素必须都有象且唯一;⑵B中元素不一定都有原象,但原象不一定唯一。如(1)设 是集合
是集合 到
到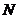 的映射,下列说法正确的是 A、
的映射,下列说法正确的是 A、 中每一个元素在
中每一个元素在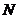 中必有象 B、
中必有象 B、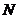 中每一个元素在
中每一个元素在 中必有原象 C、
中必有原象 C、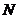 中每一个元素在
中每一个元素在 中的原象是唯一的 D、
中的原象是唯一的 D、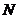 是
是 中所在元素的象的集合(答:A);(2)点
中所在元素的象的集合(答:A);(2)点 在映射
在映射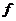 的作用下的象是
的作用下的象是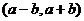 ,则在
,则在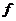 作用下点
作用下点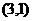 的原象为点________(答:(2,-1));(3)若
的原象为点________(答:(2,-1));(3)若 ,
,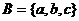 ,
,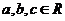 ,则
,则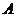 到
到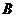 的映射有 个,
的映射有 个,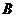 到
到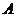 的映射有 个,
的映射有 个,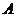 到
到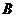 的函数有 个(答:81,64,81);(4)设集合
的函数有 个(答:81,64,81);(4)设集合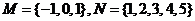 ,映射
,映射 满足条件“对任意的
满足条件“对任意的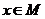 ,
,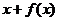 是奇数”,这样的映射
是奇数”,这样的映射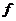 有____个(答:12);(5)设
有____个(答:12);(5)设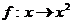 是集合A到集合B的映射,若B={1,2},则
是集合A到集合B的映射,若B={1,2},则 一定是_____(答:
一定是_____(答: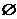 或{1}).
或{1}).
30、你熟悉下列结论吗?
⑴三个平面两两相交得到三条交线,如果其中的两条交线交于一点,那么第三条交线也经过这一点;
⑵从一点O出发的三条射线OA、OB、OC,若∠AOB=∠AOC,则点A在平面∠BOC上的射影在∠BOC的平分线上;
⑶AB和平面所成的角是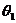 ,AC在平面内,AC和AB的射影
,AC在平面内,AC和AB的射影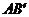 成
成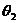 ,设∠BAC=
,设∠BAC= ,则cos
,则cos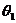 cos
cos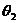 =cos
=cos ;
;
⑷如果两个相交平面都与第三个平面垂直,那么它们的交线也垂直于第三个平面;
⑸若长方体的体对角线与过同一顶点的三条棱所成的角分别为 ,则cos2
,则cos2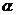 +
+
cos2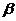 +cos2
+cos2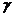 =1;若长方体的体对角线与过同一顶点的三侧面所成的角分别为
=1;若长方体的体对角线与过同一顶点的三侧面所成的角分别为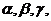 则cos2
则cos2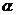 +cos2
+cos2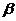 +cos2
+cos2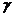 =2。如(1)长方体中若一条对角线与过同一顶点的三个面中的二个面所成的角为30°、45°,则与第三个面所成的角为____________(答:30°);(2)若一条对角线与过同一顶点的三条棱所成的角分别为
=2。如(1)长方体中若一条对角线与过同一顶点的三个面中的二个面所成的角为30°、45°,则与第三个面所成的角为____________(答:30°);(2)若一条对角线与过同一顶点的三条棱所成的角分别为 ,则
,则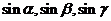 的关系为____________。(答:
的关系为____________。(答: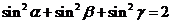 )
)
⑹若正棱锥的侧面与底面所成的角为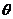 ,则
,则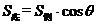 。如若正三棱锥的一个侧面的面积与底面面积之比为,则这个三棱锥的侧面和底面所成的二面角等于__(答:
。如若正三棱锥的一个侧面的面积与底面面积之比为,则这个三棱锥的侧面和底面所成的二面角等于__(答: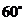 )
)
⑺在三棱锥中:①侧棱长相等(侧棱与底面所成角相等) 顶点在底上射影为底面外心;②侧棱两两垂直(两对对棱垂直)
顶点在底上射影为底面外心;②侧棱两两垂直(两对对棱垂直) 顶点在底上射影为底面垂心;③顶点到底面三角形各边的距离相等(侧面与底面所成角相等)且顶点在底面上的射影在底面三角形内
顶点在底上射影为底面垂心;③顶点到底面三角形各边的距离相等(侧面与底面所成角相等)且顶点在底面上的射影在底面三角形内 顶点在底上射影为底面内心.提醒:③若顶点在底面上的射影在底面三角形外,则顶点在底上射影为底面的旁心。
顶点在底上射影为底面内心.提醒:③若顶点在底面上的射影在底面三角形外,则顶点在底上射影为底面的旁心。
⑻正方体和长方体的外接球的直径等与其体对角线长;正四面体的外接球半径R与内切球半径r之比为R:r=3:1。
29、立体几何问题的求解策略是通过降维,转化为平面几何问题,具体方法表现为:
(1)求空间角、距离,归到三角形中求解;
(2)对于球的内接外切问题,作适当的截面――既要能反映出位置关系,又要反映出数量关系。如(1)甲球与某立方体的各个面都相切,乙球与这个立方体的各条棱都相切,丙球过这个立方体的所有顶点,则甲、乙、丙三球的半径的平方之比为_____(答:1∶2∶3);(2)若正四面体的棱长为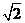 ,则此正四面体的外接球的表面积为_____(答:
,则此正四面体的外接球的表面积为_____(答: );(3)已知一个半径为
);(3)已知一个半径为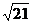 的球中有一个各条棱长都相等的内接正三棱柱,则这一正三棱柱的体积是_____(答:
的球中有一个各条棱长都相等的内接正三棱柱,则这一正三棱柱的体积是_____(答: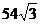 );
);
(3)求曲面上两点之间的最短距离,通过化曲为直转化为同一平面上两点间的距离。如已知正方体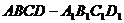 的棱长为1,
的棱长为1,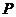 是
是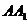 的中点,
的中点, 是
是 上的一点,则
上的一点,则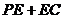 的最小值是_____(答:
的最小值是_____(答: );
);
28、球的体积和表面积公式:V=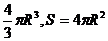 。如(1)在球内有相距9cm的两个平行截面,面积分别为49
。如(1)在球内有相距9cm的两个平行截面,面积分别为49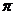 cm2、400
cm2、400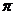 cm2,则球的表面积为______(答:
cm2,则球的表面积为______(答: );(2)三条侧棱两两垂直且长都为1的三棱锥P-ABC内接于球O,求球O的表面积与体积。
);(2)三条侧棱两两垂直且长都为1的三棱锥P-ABC内接于球O,求球O的表面积与体积。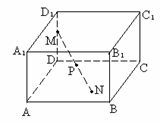 (答:表面积
(答:表面积 ,体积
,体积 );(3)已知直平行六面体
);(3)已知直平行六面体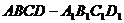 的各条棱长均为3,
的各条棱长均为3,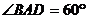 ,长为2的线段
,长为2的线段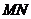 的一个端点
的一个端点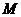 在
在 上运动,另一端点
上运动,另一端点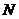 在底面
在底面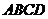 上运动,则
上运动,则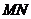 的中点
的中点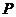 的轨迹(曲面)与共一顶点
的轨迹(曲面)与共一顶点 的三个面所围成的几何体的体积为为______(答:
的三个面所围成的几何体的体积为为______(答: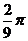 );
);
27、球的截面的性质:用一个平面去截球,截面是圆面;球心和截面圆的距离d与球的半径R及截面圆半径r之间的关系是r= 。提醒:球与球面的区别(球不仅包括球面,还包括其内部)。如(1)在半径为10
。提醒:球与球面的区别(球不仅包括球面,还包括其内部)。如(1)在半径为10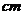 的球面上有
的球面上有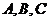 三点,如果
三点,如果 ,则球心
,则球心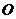 到平面
到平面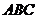 的距离为______(答:
的距离为______(答: );(2)已知球面上的三点A、B、C,AB=6,BC=8,AC=10,球的半径为13,则球心到平面ABC的距离为______(答:12)
);(2)已知球面上的三点A、B、C,AB=6,BC=8,AC=10,球的半径为13,则球心到平面ABC的距离为______(答:12)
26、正多面体:(1)定义:每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体。(2)正多面体的种类:只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种。其中正四面体、正八面体和正二十面体的每个面都是正三角形,正六面体的每个面都是正方形,正十二面体的每个面都是正五形边,如下图:



正四面体 正六面体 正八面体 正十二面体 正二十面体
25、体积:
(1)棱柱:体积=底面积×高,或体积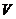 =直截面面积×侧棱长,特别地,直棱柱的体积=底面积×侧棱长;三棱柱的体积
=直截面面积×侧棱长,特别地,直棱柱的体积=底面积×侧棱长;三棱柱的体积 (其中
(其中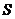 为三棱柱一个侧面的面积,
为三棱柱一个侧面的面积,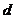 为与此侧面平行的侧棱到此侧面的距离)。如(1)设长方体的三条棱长分别为a、b、c,若长方体所有棱的长度之和为24,一条对角线长度为5,体积为2,则
为与此侧面平行的侧棱到此侧面的距离)。如(1)设长方体的三条棱长分别为a、b、c,若长方体所有棱的长度之和为24,一条对角线长度为5,体积为2,则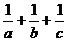 等于__(答:);(2)斜三棱柱
等于__(答:);(2)斜三棱柱 的底面是边长为
的底面是边长为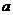 的正三角形,侧棱长为
的正三角形,侧棱长为 ,侧棱AA1和AB、AC都成45°的角,则棱柱的侧面积为___,体积为___(答:
,侧棱AA1和AB、AC都成45°的角,则棱柱的侧面积为___,体积为___(答: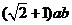 ;
;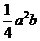 )。
)。
 (2)棱锥:体积=
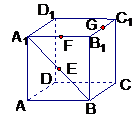
(2)棱锥:体积=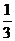 ×底面积×高。如(1)已知棱长为1的正方体容器ABCD-A1B1C1D1中,在A1B、A1B1、B1C1的中点E、F、G处各开有一个小孔,若此容器可以任意放置,则装水较多的容积(小孔面积对容积的影响忽略不计)是_____(答:
×底面积×高。如(1)已知棱长为1的正方体容器ABCD-A1B1C1D1中,在A1B、A1B1、B1C1的中点E、F、G处各开有一个小孔,若此容器可以任意放置,则装水较多的容积(小孔面积对容积的影响忽略不计)是_____(答: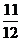 );(2)在正三棱锥A-BCD中,E、F是AB、BC的中点,EF⊥DE,若BC=
);(2)在正三棱锥A-BCD中,E、F是AB、BC的中点,EF⊥DE,若BC=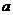 ,则正三棱锥A-BCD的体积为__(答:
,则正三棱锥A-BCD的体积为__(答: );(3)已知正三棱锥
);(3)已知正三棱锥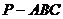 底面边长为
底面边长为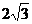 ,体积为
,体积为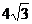 ,则底面三角形
,则底面三角形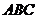 的中心
的中心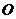 到侧面
到侧面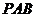 的距离为___(答:
的距离为___(答: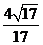 );(4)在平面几何中有:Rt△ABC的直角边分别为a,b,斜边上的高为h,则
);(4)在平面几何中有:Rt△ABC的直角边分别为a,b,斜边上的高为h,则 。类比这一结论,在三棱锥P-ABC中,PA、PB、PC两点互相垂直,且PA=a,PB=b,PC=c,此三棱锥P-ABC的高为h,则结论为______________(答:
。类比这一结论,在三棱锥P-ABC中,PA、PB、PC两点互相垂直,且PA=a,PB=b,PC=c,此三棱锥P-ABC的高为h,则结论为______________(答: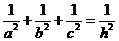 ).
).
 特别提醒:求多面体体积的常用技巧是割补法(割补成易求体积的多面体。补形:三棱锥
特别提醒:求多面体体积的常用技巧是割补法(割补成易求体积的多面体。补形:三棱锥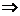 三棱柱
三棱柱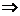 平行六面体;分割:三棱柱中三棱锥、四棱锥、三棱柱的体积关系是 (答:1:2:3)和等积变换法(平行换点、换面)和比例(性质转换)法等.如(1)用平面去截三棱锥
平行六面体;分割:三棱柱中三棱锥、四棱锥、三棱柱的体积关系是 (答:1:2:3)和等积变换法(平行换点、换面)和比例(性质转换)法等.如(1)用平面去截三棱锥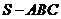 ,与三条侧棱交于
,与三条侧棱交于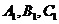 三点,若
三点,若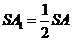 ,
,
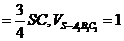 ,则多面体
,则多面体 的体积为_____(答:7);(2)直三棱柱ABC-A1B1C1的体积为
的体积为_____(答:7);(2)直三棱柱ABC-A1B1C1的体积为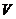 ,P、Q分别是侧棱AA1、CC1上的点,且AP=C1Q,则四棱锥B-APQC的体积为 (答:
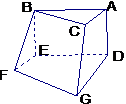
,P、Q分别是侧棱AA1、CC1上的点,且AP=C1Q,则四棱锥B-APQC的体积为 (答: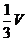 );(3)如图的多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥DEFG,平面BEF∥ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为________(答:4)。
);(3)如图的多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥DEFG,平面BEF∥ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为________(答:4)。
24、侧面积(各个侧面面积之和):
(1)棱柱:侧面积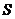 =直截面(与各侧棱都垂直相交的截面)周长×侧棱长,特别地,直棱柱的侧面积
=直截面(与各侧棱都垂直相交的截面)周长×侧棱长,特别地,直棱柱的侧面积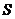 =底面周长×侧棱长。如(1)长方体的高为h,底面积为Q,垂直于底的对角面的面积为M,则此长方体的侧面积为______(答:
=底面周长×侧棱长。如(1)长方体的高为h,底面积为Q,垂直于底的对角面的面积为M,则此长方体的侧面积为______(答: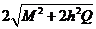 );(2)斜三棱柱ABC-
A1B1C1中,二面角C-A1A-B为120°,侧棱AA1于另外两条棱的距离分别为7cm、8cm,AA1=12cm,则斜三棱柱的侧面积为______(答:
);(2)斜三棱柱ABC-
A1B1C1中,二面角C-A1A-B为120°,侧棱AA1于另外两条棱的距离分别为7cm、8cm,AA1=12cm,则斜三棱柱的侧面积为______(答: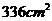 );(3)若斜三棱柱的高为4,侧棱与底面所成的角为60°,相邻两侧棱之间的距离都为5,则该三棱柱的侧面积为______(答:120)。
);(3)若斜三棱柱的高为4,侧棱与底面所成的角为60°,相邻两侧棱之间的距离都为5,则该三棱柱的侧面积为______(答:120)。
(2)正棱锥:正棱锥的侧面积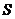 =
=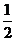 ×底面周长×斜高。如(1)已知正四棱锥P-ABCD的高为4,侧棱与底面所成的角为60°,则该正四棱锥的侧面积是_______(答:
×底面周长×斜高。如(1)已知正四棱锥P-ABCD的高为4,侧棱与底面所成的角为60°,则该正四棱锥的侧面积是_______(答: );(2)已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T,则等于______(答:)。
);(2)已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T,则等于______(答:)。
提醒:全面积(也称表面积)是各个表面面积之和,故棱柱的全面积=侧面积+2×底面积;棱锥的全面积=侧面积+底面积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com