
79.(08江苏镇江28题)(本小题满分8分)探索研究
 如图,在直角坐标系
如图,在直角坐标系 中,点
中,点 为函数
为函数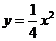 在第一象限内的图象上的任一点,点
在第一象限内的图象上的任一点,点 的坐标为
的坐标为 ,直线
,直线 过
过 且与
且与 轴平行,过
轴平行,过 作
作 轴的平行线分别交
轴的平行线分别交 轴,
轴, 于
于 ,连结
,连结 交
交 轴于
轴于 ,直线
,直线 交
交 轴于
轴于 .
.
(1)求证: 点为线段
点为线段 的中点;
的中点;
(2)求证:①四边形 为平行四边形;
为平行四边形;
②平行四边形 为菱形;
为菱形;
(3)除 点外,直线
点外,直线 与抛物线
与抛物线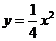 有无其它公共点?并说明理由.
有无其它公共点?并说明理由.
(08江苏镇江28题解析)(1)法一:由题可知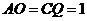 .
.
 ,
, ,
,
 .························································································· (1分)
.························································································· (1分)
 ,即
,即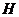 为
为 的中点.····································································· (2分)
的中点.····································································· (2分)
法二: ,
, ,
,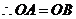 .·························································· (1分)
.·························································· (1分)
又 轴,
轴, .··············································································· (2分)
.··············································································· (2分)
(2)①由(1)可知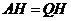 ,
, ,
,
 ,
, ,
,
 .·························································································· (3分)
.·························································································· (3分)
 ,
,
又 ,
, 四边形
四边形 为平行四边形.···················································· (4分)
为平行四边形.···················································· (4分)
②设 ,
, 轴,则
轴,则 ,则
,则 .
.
过 作
作 轴,垂足为
轴,垂足为 ,在
,在 中,
中,
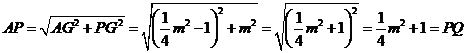 .
.
 平行四边形
平行四边形 为菱形.··············································································· (6分)
为菱形.··············································································· (6分)
(3)设直线 为
为 ,由
,由 ,得
,得 ,
, 代入得:
代入得:


 直线
直线 为
为 .························ (7分)
.························ (7分)
设直线 与抛物线的公共点为
与抛物线的公共点为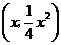 ,代入直线
,代入直线 关系式得:
关系式得:
 ,
, ,解得
,解得 .得公共点为
.得公共点为 .
.
所以直线 与抛物线
与抛物线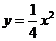 只有一个公共点
只有一个公共点 .············································· (8分)
.············································· (8分)
80(08黑龙江齐齐哈尔28题)(本小题满分10分)
如图,在平面直角坐标系中,点 ,点
,点 分别在
分别在 轴,
轴, 轴的正半轴上,且满足
轴的正半轴上,且满足 .
.
(1)求点 ,点
,点 的坐标.
的坐标.
(2)若点 从
从 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线 运动,连结
运动,连结 .设
.设 的面积为
的面积为 ,点
,点 的运动时间为
的运动时间为 秒,求
秒,求 与
与 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点 ,使以点
,使以点 为顶点的三角形与
为顶点的三角形与 相似?若存在,请直接写出点
相似?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(08黑龙江齐齐哈尔28题解析)解:(1)
 ,
, ··················································································· (1分)
··················································································· (1分)
 ,
,

 点
点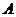 ,点
,点 分别在
分别在 轴,
轴, 轴的正半轴上
轴的正半轴上
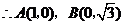 ······························································································· (2分)
······························································································· (2分)
(2)求得 ························································································· (3分)
························································································· (3分)

(每个解析式各1分,两个取值范围共1分)························································· (6分)
(3) ;
; ;
; ;
; (每个1分,计4分)
(每个1分,计4分)
···························································································································· (10分)
81(08海南省卷24题)(本题满分14分)如图13,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;(2)求证:① CB=CE ;② D是BE的中点;
 (3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
(08海南省卷24题解析)(1)∵ 点B(-2,m)在直线y=-2x-1上,
∴ m=-2×(-2)-1=3. ………………………………(2分)
∴ B(-2,3)
∵ 抛物线经过原点O和点A,对称轴为x=2,
∴ 点A的坐标为(4,0) .
设所求的抛物线对应函数关系式为y=a(x-0)(x-4). ……………………(3分)
将点B(-2,3)代入上式,得3=a(-2-0)(-2-4),∴  .
.
∴ 所求的抛物线对应的函数关系式为 ,即
,即 . (6分)
. (6分)
(2)①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1) E(2,-5).
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,
 则BG⊥直线x=2,BG=4.
则BG⊥直线x=2,BG=4.
在Rt△BGC中,BC= .
.
∵ CE=5,
∴ CB=CE=5. ……………………(9分)
②过点E作EH∥x轴,交y轴于H,
则点H的坐标为H(0,-5).
又点F、D的坐标为F(0,3)、D(0,-1),
∴ FD=DH=4,BF=EH=2,∠BFD=∠EHD=90°.
∴ △DFB≌△DHE (SAS),
∴ BD=DE.
即D是BE的中点. ………………………………(11分)
(3) 存在. ………………………………(12分)
由于PB=PE,∴ 点P在直线CD上,
∴ 符合条件的点P是直线CD与该抛物线的交点.
设直线CD对应的函数关系式为y=kx+b.
将D(0,-1) C(2,0)代入,得 . 解得
. 解得  .
.
∴ 直线CD对应的函数关系式为y= x-1.
x-1.
∵ 动点P的坐标为(x, ),
),
∴  x-1=
x-1= .
………………………………(13分)
.
………………………………(13分)
解得  ,
, .
∴
.
∴
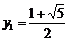 ,
, .
.
∴ 符合条件的点P的坐标为( ,
, )或(
)或(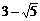 ,
, ).…(14分)
).…(14分)
71.(08湖北十堰25题) 已知抛物线
已知抛物线 与
与 轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
⑴直接写出抛物线的对称轴,及抛物线与 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
⑵当点C在以AB为直径的⊙P上时,求抛物线的解析式;
⑶坐标平面内是否存在点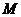 ,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点
,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点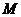 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

(08湖北十堰25题解析)解:⑴对称轴是直线: ,点B的坐标是(3,0). ……2分
,点B的坐标是(3,0). ……2分
说明:每写对1个给1分,“直线”两字没写不扣分.
⑵如图,连接PC,∵点A、B的坐标分别是A(-1,0)、B (3,0),
∴AB=4.∴
在Rt△POC中,∵OP=PA-OA=2-1=1,
∴
∴b= ………………………………3分
………………………………3分
当 时,
时,
∴ ………………………………4分
………………………………4分
∴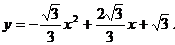 ………………5分
………………5分
⑶存在.……………………………6分
理由:如图,连接AC、BC.设点M的坐标为 .
.
①当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB.
由⑵知,AB=4,∴|x|=4,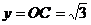 .
.
∴x=±4.∴点M的坐标为 .…9分
.…9分
说明:少求一个点的坐标扣1分.
②当以AB为对角线时,点M在x轴下方.
过M作MN⊥AB于N,则∠MNB=∠AOC=90°.
∵四边形AMBC是平行四边形,∴AC=MB,且AC∥MB.
∴∠CAO=∠MBN.∴△AOC≌△BNM.∴BN=AO=1,MN=CO= .
.
∵OB=3,∴0N=3-1=2.
∴点M的坐标为 .
……………………………12分
.
……………………………12分
说明:求点M的坐标时,用解直角三角形的方法或用先求直线解析式,
然后求交点M的坐标的方法均可,请参照给分.
综上所述,坐标平面内存在点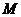 ,使得以点A、B、C、M为顶点的四边形是平行四边形.其坐标为
,使得以点A、B、C、M为顶点的四边形是平行四边形.其坐标为 .
.
说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分。

72(08湖南株洲23题)如图(1),在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数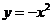 的图象为
的图象为 .
.
(1)平移抛物线 ,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可).
,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可).
(2)平移抛物线 ,使平移后的抛物线过A、B两点,记抛物线为
,使平移后的抛物线过A、B两点,记抛物线为 ,如图(2),求抛物线
,如图(2),求抛物线 的函数解析式及顶点C的坐标.
的函数解析式及顶点C的坐标.
(3)设P为y轴上一点,且 ,求点P的坐标.
,求点P的坐标.
(4)请在图(2)上用尺规作图的方式探究抛物线 上是否存在点Q,使
上是否存在点Q,使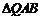 为等腰三角形.
若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
为等腰三角形.
若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.

(08湖南株洲23题解析)
(1) 等 (满足条件即可)
……1分
等 (满足条件即可)
……1分
(2)设 的解析式为
的解析式为 ,联立方程组
,联立方程组 ,
,
解得: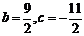 ,则
,则 的解析式为
的解析式为 ……3分
……3分
点C的坐标为( )
……4分
)
……4分
(3)如答图23-1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,则 ,
, ,
,
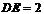

 得:
得: .
……5分 延长BA交y轴于点G,直线AB的解析式为
.
……5分 延长BA交y轴于点G,直线AB的解析式为 ,则点G的坐标为(0,
,则点G的坐标为(0, ),设点P的坐标为(0,
),设点P的坐标为(0, )
)
①当点P位于点G的下方时, ,连结AP、BP,则
,连结AP、BP,则 ,又
,又 ,得
,得 ,点P的坐标为(0,
,点P的坐标为(0, ).
…… 6分
).
…… 6分
②当点P位于点G的上方时, ,同理
,同理 ,点P的坐标为(0,
,点P的坐标为(0, ).
).
综上所述所求点P的坐标为(0, )或(0,
)或(0, )
…… 7分
)
…… 7分
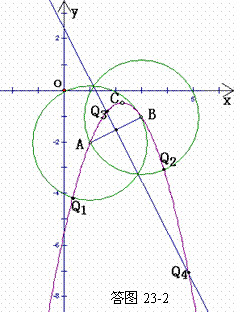
 (4) 作图痕迹如答图23-2所示. 由图可知,满足条件的点有
(4) 作图痕迹如答图23-2所示. 由图可知,满足条件的点有 、
、 、
、 、
、 ,共4个可能的位置. …… 10分
,共4个可能的位置. …… 10分
73(08四川达州23题)如图,将 置于平面直角坐标系中,其中点
置于平面直角坐标系中,其中点 为坐标原点,点
为坐标原点,点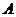 的坐标为
的坐标为 ,
,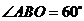 .
.
(1)若 的外接圆与
的外接圆与 轴交于点
轴交于点 ,求
,求 点坐标.
点坐标.
(2)若点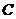 的坐标为
的坐标为 ,试猜想过
,试猜想过 的直线与
的直线与 的外接圆的位置关系,并加以说明.
的外接圆的位置关系,并加以说明.
(3)二次函数的图象经过点 和
和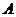 且顶点在圆上,
且顶点在圆上,
求此函数的解析式.

(08四川达州23题解析)解:(1)连结AD,则∠ADO=∠B=600
在Rt△ADO中,∠ADO=600
所以OD=OA÷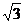 =3÷
=3÷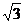 =
=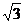

|
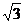 )
)
(2)猜想是CD与圆相切
∵ ∠AOD是直角,所以AD是圆的直径
|
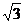 =
=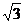 , ∠CDO=300
, ∠CDO=300
∴∠CDA=∠CDO+∠ADO=Rt∠ 即CD⊥AD
∴ CD切外接圆于点D
(3)依题意可设二次函数的解析式为 :
y=α(x-0)(x-3)
 由此得顶点坐标的横坐标为:x=
由此得顶点坐标的横坐标为:x= =
= ;
;
即顶点在OA的垂直平分线上,作OA的垂直平分线EF,则得∠EFA= ∠B=300
∠B=300
得到EF=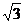 EA=
EA= 可得一个顶点坐标为(
可得一个顶点坐标为( ,
, )
)
同理可得另一个顶点坐标为( ,
, )
)
分别将两顶点代入y=α(x-0)(x-3)可解得α的值分别为 ,
,
则得到二次函数的解析式是y= x(x-3)或y=
x(x-3)或y= x(x-3)
x(x-3)
74(08安徽芜湖24题)如图,已知  ,
, ,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
(1) 求C点坐标及直线BC的解析式;
(2) 一抛物线经过B、C两点,且顶点落在x轴正半轴上,求该抛物线的解析式并画出函数图象;
(3)
现将直线BC绕B点旋转与抛物线相交与另一点P,请找出抛物线上所有满足到直线AB距离为 的点P.
的点P.
 解
解
(08安徽芜湖24题解析)解: (1)
过C点向x轴作垂线,垂足为D,由位似图形性质可知:
△ABO∽△ACD, ∴ .
.
由已知 ,
, 可知:
可知:  .
.
∴ .∴C点坐标为
.∴C点坐标为 .·················· 2分
.·················· 2分
直线BC的解析是为: 
化简得:  ·················································· 3分
·················································· 3分
(2)设抛物线解析式为 ,由题意得:
,由题意得: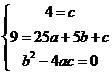 ,
,
解得:  ,
,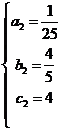
∴解得抛物线解析式为 或
或 .
.
又∵ 的顶点在x轴负半轴上,不合题意,故舍去.
的顶点在x轴负半轴上,不合题意,故舍去.
∴满足条件的抛物线解析式为 ······························································· 5分
······························································· 5分
(准确画出函数 图象)········································································· 7分
图象)········································································· 7分
(3) 将直线BC绕B点旋转与抛物线相交与另一点P,设P到 直线AB的距离为h,
故P点应在与直线AB平行,且相距 的上下两条平行直线
的上下两条平行直线 和
和 上.······················ 8分
上.······················ 8分
由平行线的性质可得:两条平行直线与y轴的交点到直线BC的距离也为 .
.
如图,设 与y轴交于E点,过E作EF⊥BC于F点,
与y轴交于E点,过E作EF⊥BC于F点,
在Rt△BEF中 ,
,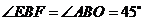 ,
,
∴ .∴可以求得直线
.∴可以求得直线 与y轴交点坐标为
与y轴交点坐标为 ·············································· 10分
·············································· 10分
同理可求得直线 与y轴交点坐标为
与y轴交点坐标为 ································································· 11分
································································· 11分
∴两直线解析式 ;
; .
.
根据题意列出方程组: ⑴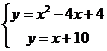 ;⑵
;⑵
∴解得: ;
; ;
; ;
;
∴满足条件的点P有四个,它们分别是 ,
, ,
, ,
, ········ 15分
········ 15分
75(08湖北仙桃等4市25题)如图,直角梯形 中,
中,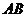 ∥
∥ ,
, 为坐标原点,点
为坐标原点,点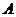 在
在 轴正半轴上,点
轴正半轴上,点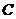 在
在 轴正半轴上,点
轴正半轴上,点 坐标为(2,2
坐标为(2,2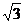 ),∠
),∠ = 60°,
= 60°, 于点
于点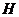 .动点
.动点 从点
从点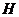 出发,沿线段
出发,沿线段 向点
向点 运动,动点
运动,动点 从点
从点 出发,沿线段
出发,沿线段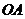 向点
向点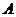 运动,两点同时出发,速度都为每秒1个单位长度.设点
运动,两点同时出发,速度都为每秒1个单位长度.设点 运动的时间为
运动的时间为 秒.
秒.
(1)求 的长;
的长;
 (2)若
(2)若 的面积为
的面积为 (平方单位). 求
(平方单位). 求 与
与 之间的函数关系式.并求
之间的函数关系式.并求 为何值时,
为何值时, 的面积最大,最大值是多少?
的面积最大,最大值是多少?
(3)设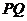 与
与 交于点
交于点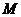 .①当△
.①当△ 为等腰三角形时,求(2)中
为等腰三角形时,求(2)中 的值.
的值.
②探究线段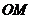 长度的最大值是多少,直接写出结论.
长度的最大值是多少,直接写出结论.

(08湖北仙桃等4市25题解析)解:(1)∵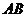 ∥
∥
∴ 
在 中,
中, ,
,
∴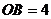 ,
, 
∴ 而
而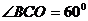
∴ 为等边三角形
为等边三角形
∴ …(3分)
…(3分)
(2)∵
∴

∴
= (
( )…………………………(6分)
)…………………………(6分)
即
 ∴当
∴当 时,
时,
 ………………………………………(7分)
………………………………………(7分)
(3)①若 为等腰三角形,则:
为等腰三角形,则:
(i)若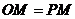 ,
,
∴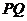 ∥
∥
∴ 即
即
解得:
 此时
此时 ………………………………(8分)
………………………………(8分)
(ii)若 ,
,
∴
过 点作
点作 ,垂足为
,垂足为 ,则有:
,则有:
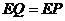
即
解得:
此时 ……………………………………(9分)
……………………………………(9分)
(iii)若 ,
,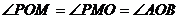
∴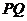 ∥
∥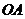
此时 在
在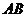 上,不满足题意.……………………………………………(10分)
上,不满足题意.……………………………………………(10分)
②线段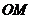 长的最大值为
长的最大值为 ……………………………………………………(12分)
……………………………………………………(12分)
76(08湖南常德26题)如图9,在直线 上摆放有△ABC和直角梯形DEFG,且CD=6㎝;在△ABC中:∠C=90O,∠A=300,AB=4㎝;在直角梯形DEFG中:EF//DG,∠DGF=90O ,DG=6㎝,DE=4㎝,∠EDG=600。解答下列问题:
上摆放有△ABC和直角梯形DEFG,且CD=6㎝;在△ABC中:∠C=90O,∠A=300,AB=4㎝;在直角梯形DEFG中:EF//DG,∠DGF=90O ,DG=6㎝,DE=4㎝,∠EDG=600。解答下列问题:
(1)旋转:将△ABC绕点C顺时针方向旋转900,请你在图中作出旋转后的对应图形
△A1B1C,并求出AB1的长度;
(2)翻折:将△A1B1C沿过点B1且与直线 垂直的直线翻折,得到翻折后的对应图形
垂直的直线翻折,得到翻折后的对应图形
△A2B1C1,试判定四边形A2B1DE的形状?并说明理由;
 (3)平移:将△A2B1C1沿直线
(3)平移:将△A2B1C1沿直线 向右平移至△A3B2C2,若设平移的距离为x,△A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC面积的一半时,x的值是多少?
向右平移至△A3B2C2,若设平移的距离为x,△A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC面积的一半时,x的值是多少?
(08湖南常德26题解析)
解:(1)在△ABC中由已知得:BC=2,AC=AB×cos30°=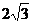 ,
,
∴AB1=AC+C B1=AC+CB= .……………………………………2分
.……………………………………2分
(2)四边形A2B1DE为平行四边形.理由如下:
∵∠EDG=60°,∠A2B1C1=∠A1B1C=∠ABC=60°,∴A2B1∥DE
又A2B1=A1B1=AB=4,DE=4,∴A2B1=DE,故结论成立.………………4分
(3)由题意可知:
S△ABC= ,
,
①
当 或
或 时,y=0
时,y=0
此时重叠部分的面积不会等于△ABC的面积的一半……………5分
②当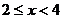 时,直角边B2C2与等腰梯形的下底边DG重叠的长度为DC2=C1C2-DC1=(x-2)㎝,则y=
时,直角边B2C2与等腰梯形的下底边DG重叠的长度为DC2=C1C2-DC1=(x-2)㎝,则y= ,
,
当y=  S△ABC=
S△ABC= 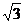 时,即
时,即  ,
,
解得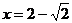 (舍)或
(舍)或 .
.
∴当 时,重叠部分的面积等于△ABC的面积的一半.
时,重叠部分的面积等于△ABC的面积的一半.
③当 时,△A3B2C2完全与等腰梯形重叠,即
时,△A3B2C2完全与等腰梯形重叠,即 ……………7分
……………7分
④当 时,B2G=B2C2-GC2=2-(
时,B2G=B2C2-GC2=2-( -8)=10-
-8)=10-
则y= ,
,
当y=  S△ABC=
S△ABC= 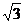 时,即
时,即  ,
,
解得 ,或
,或 (舍去).
(舍去).
∴当 时,重叠部分的面积等于△ABC的面积的一半.………9分
时,重叠部分的面积等于△ABC的面积的一半.………9分
由以上讨论知,当 或
或 时, 重叠部分的面积等于△ABC的面积的一半.………10分
时, 重叠部分的面积等于△ABC的面积的一半.………10分
77(08宁夏区卷26题)如图,在边长为4的正方形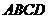 中,点
中,点 在
在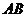 上从
上从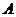 向
向 运动,连接
运动,连接 交
交 于点
于点 .
.

 (1)试证明:无论点
(1)试证明:无论点 运动到
运动到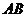 上何处时,都有△
上何处时,都有△ ≌△
≌△ ;
;
(2)当点 在
在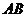 上运动到什么位置时,△
上运动到什么位置时,△ 的面积是正方形
的面积是正方形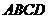 面积的
面积的 ;
;
(3)若点 从点
从点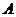 运动到点
运动到点 ,再继续在
,再继续在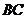 上运动到点
上运动到点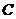 ,在整个运动过程中,当点
,在整个运动过程中,当点 运动到什么位置时,△
运动到什么位置时,△ 恰为等腰三角形.
恰为等腰三角形.
(08宁夏区卷26题解析)(1)证明:在正方形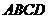 中,
中,
无论点 运动到
运动到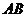 上何处时,都有
上何处时,都有
 =
=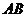 ∠
∠ =∠
=∠
 =
=
∴△ ≌△
≌△ ·············································· 2分
·············································· 2分
(2)解法一:△ 的面积恰好是正方形ABCD面积的
的面积恰好是正方形ABCD面积的 时,
时,
过点Q作
 ⊥
⊥ 于
于 ,
, ⊥
⊥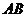 于
于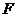 ,则
,则 =
= 

 =
= =
=
∴ =
= ·········································································································· 4分
·········································································································· 4分
由△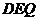 ∽△
∽△ 得
得
 解得
解得
∴ 时,△
时,△ 的面积是正方形
的面积是正方形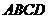 面积的
面积的 ······························· 6分
······························· 6分
解法二:以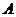 为原点建立如图所示的直角坐标系,过点
为原点建立如图所示的直角坐标系,过点 作
作 ⊥
⊥ 轴于点
轴于点 ,
, ⊥
⊥ 轴于点
轴于点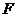 .
.


 =
= =
= ∴
∴ =
=
∵点 在正方形对角线
在正方形对角线 上 ∴
上 ∴ 点的坐标为
点的坐标为
∴ 过点 (0,4),
(0,4), (
( 两点的函数关系式为:
两点的函数关系式为:
当 时,
时, ∴
∴ 点的坐标为(2,0)
点的坐标为(2,0)
∴ 时,△
时,△ 的面积是正方形
的面积是正方形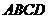 面积的
面积的 . ······························· 6分
. ······························· 6分
(3)若△ 是等腰三角形,则有
是等腰三角形,则有  =
= 或
或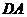 =
= 或
或 =
=
 ①当点
①当点 运动到与点
运动到与点 重合时,由四边形
重合时,由四边形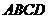 是正方形知
是正方形知  =
=
此时△ 是等腰三角形
是等腰三角形
②当点 与点
与点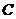 重合时,点
重合时,点 与点
与点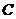 也重合,
也重合,
此时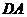 =
= , △
, △ 是等腰三角形 ································· 8分
是等腰三角形 ································· 8分
③解法一:如图,设点 在
在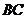 边上运动到
边上运动到 时,有
时,有 =
=
∵  ∥
∥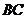 ∴∠
∴∠ =∠
=∠
又∵∠ =∠
=∠ ∠
∠ =∠
=∠
∴∠ =∠
=∠
∴  =
=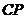 =
=
∵ =
=
 =
=  =4
=4
∴
即当 时,△
时,△ 是等腰三角形 ····································· 10分
是等腰三角形 ····································· 10分
解法二:以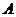 为原点建立如图所示的直角坐标系,设点
为原点建立如图所示的直角坐标系,设点 在
在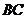 上运动到
上运动到 时,有
时,有 =
= .
.
过点 作
作 ⊥
⊥ 轴于点
轴于点 ,
, ⊥
⊥ 轴于点
轴于点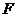 ,则
,则
在 △
△ 中,
中, ,∠
,∠ =45°
=45°
 ∴
∴试题详情
70.(08河北省卷26题)如图15,在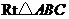 中,
中, ,
, ,
, ,
, 分别是
分别是 的中点.点
的中点.点 从点
从点 出发沿折线
出发沿折线 以每秒7个单位长的速度匀速运动;点
以每秒7个单位长的速度匀速运动;点 从点
从点 出发沿
出发沿 方向以每秒4个单位长的速度匀速运动,过点
方向以每秒4个单位长的速度匀速运动,过点 作射线
作射线 ,交折线
,交折线 于点
于点 .点
.点 同时出发,当点
同时出发,当点 绕行一周回到点
绕行一周回到点 时停止运动,点
时停止运动,点 也随之停止.设点
也随之停止.设点 运动的时间是
运动的时间是 秒(
秒( ).
).
(1) 两点间的距离是
;
两点间的距离是
;
(2)射线 能否把四边形
能否把四边形 分成面积相等的两部分?若能,求出
分成面积相等的两部分?若能,求出 的值.若不能,说明理由;
的值.若不能,说明理由;
(3)当点 运动到折线
运动到折线 上,且点
上,且点 又恰好落在射线
又恰好落在射线 上时,求
上时,求 的值;
的值;
 (4)连结
(4)连结 ,当
,当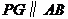 时,请直接写出
时,请直接写出 的值.
的值.
(08河北省卷26题解析)解:(1)25.
(2)能.
如图5,连结 ,过点
,过点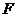 作
作 于点
于点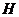 ,
,
由四边形 为矩形,可知
为矩形,可知 过
过 的中点
的中点 时,
时,
 把矩形
把矩形 分为面积相等的两部分
分为面积相等的两部分
(注:可利用全等三角形借助割补法或用中心对称等方法说明),
此时 .由
.由 ,
, ,得
,得 .
.
 故
故 .
.
(3)①当点 在
在 上
上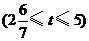 时,如图6.
时,如图6.
 ,
, ,
,
 由
由 ,得
,得 .
.
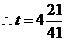 .
.
②当点 在
在 上
上 时,如图7.
时,如图7.
 已知
已知 ,从而
,从而 ,
,
由 ,
, ,得
,得 .
.
解得 .
.
(4)如图8,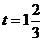 ;如图9,
;如图9, .
.

(注:判断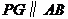 可分为以下几种情形:当
可分为以下几种情形:当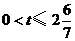 时,点
时,点 下行,点
下行,点 上行,可知其中存在
上行,可知其中存在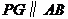 的时刻,如图8;此后,点
的时刻,如图8;此后,点 继续上行到点
继续上行到点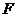 时,
时, ,而点
,而点 却在下行到点
却在下行到点 再沿
再沿 上行,发现点
上行,发现点 在
在 上运动时不存在
上运动时不存在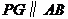 ;当
;当 时,点
时,点 均在
均在 上,也不存在
上,也不存在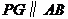 ;由于点
;由于点 比点
比点 先到达点
先到达点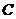 并继续沿
并继续沿 下行,所以在
下行,所以在 中存在
中存在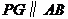 的时刻,如图9;当
的时刻,如图9;当 时,点
时,点 均在
均在 上,不存在
上,不存在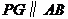 )
)
69.(08广东中山22题)将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边
AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
(1)填空:如图9,AC= ,BD= ;四边形ABCD是 梯形.
(2)请写出图9中所有的相似三角形(不含全等三角形).
(3)如图10,若以AB所在直线为 轴,过点A垂直于AB的直线为
轴,过点A垂直于AB的直线为 轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向
轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向 轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.


(08广东中山22题解析)解:(1) ,
, ,…………………………1分
,…………………………1分
等腰;…………………………2分
(2)共有9对相似三角形.(写对3-5对得1分,写对6-8对得2分,写对9对得3分)
①△DCE、△ABE与△ACD或△BDC两两相似,分别是:△DCE∽△ABE,△DCE∽△ACD,△DCE∽△BDC,△ABE∽△ACD,△ABE∽△BDC;(有5对)
②△ABD∽△EAD,△ABD∽△EBC;(有2对)
③△BAC∽△EAD,△BAC∽△EBC;(有2对)
所以,一共有9对相似三角形.…………………………………………5分

(3)由题意知,FP∥AE,
∴ ∠1=∠PFB,
又∵ ∠1=∠2=30°,
∴ ∠PFB=∠2=30°,
∴ FP=BP.…………………………6分
过点P作PK⊥FB于点K,则 .
.
∵ AF=t,AB=8,
∴ FB=8-t, .
.
在Rt△BPK中, . ……………………7分
. ……………………7分
∴ △FBP的面积 ,
,
∴ S与t之间的函数关系式为:
 ,或
,或 . …………………………………8分
. …………………………………8分
t的取值范围为: . …………………………………………………………9分
. …………………………………………………………9分
68.(08浙江杭州24) 在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二次函数 的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
(1)是否存在这样的抛物线F,使得 ?请你作出判断,并说明理由;
?请你作出判断,并说明理由;
 (2)如果AQ∥BC,且tan∠ABO=
(2)如果AQ∥BC,且tan∠ABO= ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。
(08浙江杭州24题解析)∵ 平移 的图象得到的抛物线
的图象得到的抛物线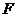 的顶点为
的顶点为 ,
,
∴ 抛物线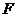 对应的解析式为:
对应的解析式为: .
--- 2分
.
--- 2分
∵ 抛物线与x轴有两个交点,∴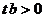 .
--- 1分
.
--- 1分
令 , 得
, 得
 ,
,
 ,
,
∴ 
 )(
)(

 )|
)|
 ,
,
即 , 所以当
, 所以当 时, 存在抛物线
时, 存在抛物线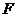 使得
使得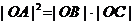 .-- 2分
.-- 2分
(2)
∵ , ∴
, ∴  ,
得
,
得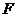 :
:  ,
,
解得 .
--- 1分
.
--- 1分
在
 中,
中,
1)
当 时,由
时,由  , 得
, 得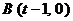 ,
,
当 时, 由
时, 由

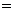

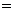
 , 解得
, 解得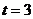 ,
,
此时, 二次函数解析式为 ;
--- 2分
;
--- 2分
当 时, 由
时, 由

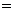

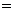
 , 解得
, 解得
 ,
,
此时,二次函数解析式为

 +
+
 +
+ .
--- 2分
.
--- 2分
2)
当 时, 由
时, 由  , 将
, 将 代
代 , 可得
, 可得
 ,
,  ,
,
(也可由 代
代 ,
,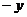 代
代 得到)
得到)
所以二次函数解析式为 

 +
+
 –
– 或
或 . --- 2分.
. --- 2分.
65.(08吉林长春27题)(12分)已知两个关于 的二次函数
的二次函数 与当
与当 时,
时, ;且二次函数
;且二次函数 的图象的对称轴是直
的图象的对称轴是直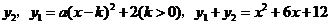 线
线 .
.
(1)求 的值;
的值;
(2)求函数 的表达式;
的表达式;
(3)在同一直角坐标系内,问函数 的图象与
的图象与 的图象是否有交点?请说明理由.
的图象是否有交点?请说明理由.
(08吉林长春27题解析)[解] (1)由
得 .
.
又因为当 时,
时, ,即
,即 ,
,
解得 ,或
,或 (舍去),故
(舍去),故 的值为
的值为 .
.
(2)由 ,得
,得 ,
,
所以函数 的图象的对称轴为
的图象的对称轴为 ,
,
于是,有 ,解得
,解得 ,
,
所以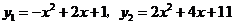 .
.
(3)由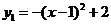 ,得函数
,得函数 的图象为抛物线,其开口向下,顶点坐标为
的图象为抛物线,其开口向下,顶点坐标为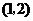 ;
;
由 ,得函数
,得函数 的图象为抛物线,其开口向上,顶点坐标为
的图象为抛物线,其开口向上,顶点坐标为 ;
;
故在同一直角坐标系内,函数 的图象与
的图象与 的图象没有交点.
的图象没有交点.
66(08江苏盐城28题)(本题满分12分)
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ▲ ,数量关系为 ▲ .
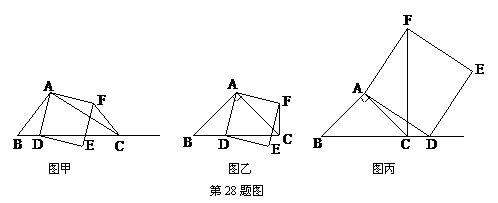 ②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90º,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若AC= ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
(08江苏盐城28题解析)(1)①CF与BD位置关系是 垂 直、数量关系是相 等;
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得 AD=AF ,∠DAF=90º.
∵∠BAC=90º,∴∠DAF=∠BAC , ∴∠DAB=∠FAC,
又AB=AC ,∴△DAB≌△FAC , ∴CF=BD
∠ACF=∠ABD.
∵∠BAC=90º, AB=AC ,∴∠ABC=45º,∴∠ACF=45º,
∴∠BCF=∠ACB+∠ACF= 90º.即 CF⊥BD
 (2)画图正确
(2)画图正确
当∠BCA=45º时,CF⊥BD(如图丁).
理由是:过点A作AG⊥AC交BC于点G,∴AC=AG
可证:△GAD≌△CAF ∴∠ACF=∠AGD=45º
∠BCF=∠ACB+∠ACF= 90º. 即CF⊥BD
(3)当具备∠BCA=45º时,
 过点A作AQ⊥BC交BC的延长线于点Q,(如图戊)
过点A作AQ⊥BC交BC的延长线于点Q,(如图戊)
∵DE与CF交于点P时, ∴此时点D位于线段CQ上,
∵∠BCA=45º,可求出AQ= CQ=4.设CD=x ,∴ DQ=4-x,
容易说明△AQD∽△DCP,∴ , ∴
, ∴ ,
,
 .
.
∵0<x≤3 ∴当x=2时,CP有最大值1.
67(08山东济南24题)(本小题满分9分)
已知:抛物线 (a≠0),顶点C (1,
(a≠0),顶点C (1, ),与x轴交于A、B两点,
),与x轴交于A、B两点, .
.
(1)求这条抛物线的解析式.
(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线对称轴交于点E,依次连接A、D、B、E,点P为线段AB上一个动点(P与A、B两点不重合),过点P作PM⊥AE于M,PN⊥DB于N,请判断 是否为定值? 若是,请求出此定值;若不是,请说明理由.
是否为定值? 若是,请求出此定值;若不是,请说明理由.
 (3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP ,FG分别与边AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断
(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP ,FG分别与边AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断 是否成立.若成立,请给出证明;若不成立,请说明理由.
是否成立.若成立,请给出证明;若不成立,请说明理由.
(08山东济南24题解析)解:(1)设抛物线的解析式为 .......... 1分
.......... 1分
将A(-1,0)代入:  ∴
∴  ..................................... 2分
..................................... 2分
∴ 抛物线的解析式为 ,即:
,即: ......................... 3分
......................... 3分
(2)是定值, ........................................................................... 4分
........................................................................... 4分
∵ AB为直径,∴ ∠AEB=90°,∵ PM⊥AE,∴ PM∥BE
∴ △APM∽△ABE,∴
 ①
①
同理:  ② .................................................................................. 5分
② .................................................................................. 5分
①
+ ②: .................................................................. 6分
.................................................................. 6分
(3)∵ 直线EC为抛物线对称轴,∴ EC垂直平分AB
∴ EA=EB
∵ ∠AEB=90°
∴ △AEB为等腰直角三角形.
∴ ∠EAB=∠EBA=45° ................... 7分
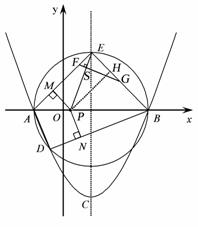 如图,过点P作PH⊥BE于H,
如图,过点P作PH⊥BE于H,
由已知及作法可知,四边形PHEM是矩形,
∴PH=ME且PH∥ME
在△APM和△PBH中
∵∠AMP=∠PHB=90°, ∠EAB=∠BPH=45°
∴ PH=BH
且△APM∽△PBH
∴

∴
 ①.................. 8分
①.................. 8分
在△MEP和△EGF中,
∵ PE⊥FG, ∴ ∠FGE+∠SEG=90°
∵∠MEP+∠SEG=90° ∴ ∠FGE=∠MEP
∵ ∠PME=∠FEG=90° ∴△MEP∽△EGF
∴ ②
②
由①、②知: .................................................................................. 9分
.................................................................................. 9分
(本题若按分类证明,只要合理,可给满分)
65、(08湖南永州25题)(10分)如图,二次函数y=ax2+bx+c(a>0)与坐标轴交于点A、B、C且OA=1,OB=OC=3 .
(1)求此二次函数的解析式.
(2)写出顶点坐标和对称轴方程.
(3)点M、N在y=ax2+bx+c的图像上(点N在点M的右边),且MN∥x轴,求以MN为直径且与x轴相切的圆的半径.
(08湖南永州25题解析)(1)依题意 分别代入
分别代入 1分
1分
解方程组得所求解析式为 ······································································ 4分
······································································ 4分
(2) ··············································································· 5分
··············································································· 5分
 顶点坐标
顶点坐标 ,对称轴
,对称轴 ················································································· 7分
················································································· 7分
(3)设圆半径为 ,当
,当 在
在 轴下方时,
轴下方时, 点坐标为
点坐标为 ····························· 8分
····························· 8分
把 点代入
点代入 得
得 ································································· 9分
································································· 9分
同理可得另一种情形
 圆的半径为
圆的半径为 或
或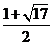 10分
10分
64、(08湖南湘潭26题)(本题满分10分)
已知抛物线 经过点A(5,0)、B(6,-6)和原点.
经过点A(5,0)、B(6,-6)和原点.
(1)求抛物线的函数关系式;
(2)若过点B的直线 与抛物线相交于点C(2,m),请求出
与抛物线相交于点C(2,m),请求出 OBC的面积S的值.
OBC的面积S的值.
 (3)过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴交x轴于点F,交直线DC于点E. 直线PF与直线DC及两坐标轴围成矩形OFED(如图),是否存在点P,使得
(3)过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴交x轴于点F,交直线DC于点E. 直线PF与直线DC及两坐标轴围成矩形OFED(如图),是否存在点P,使得 OCD与
OCD与 CPE相似?若存在,求出点P的坐标;若不存在,请说明理由.
CPE相似?若存在,求出点P的坐标;若不存在,请说明理由.
(08湖南湘潭26题解析)解:(1)由题意得: 2分
2分
解得 ·················································· 3分
·················································· 3分
故抛物线的函数关系式为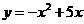 ·············· 4分
·············· 4分
(2) 在抛物线上,
在抛物线上, ·· 5分
·· 5分
 点坐标为(2,6),
点坐标为(2,6), 、C在直线
、C在直线 上
上

 解得
解得
 直线BC的解析式为
直线BC的解析式为 ······································································· 6分
······································································· 6分
设BC与x轴交于点G,则G的坐标为(4,0)
 ·································································· 7分
·································································· 7分
(3)存在P,使得 ∽
∽ ·············································································· 8分
·············································································· 8分
设P ,
,
故
若要 ∽
∽ ,则要
,则要 或
或
即 或
或
解得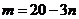 或
或
又 在抛物线上,
在抛物线上, 或
或
解得 或
或
故P点坐标为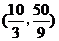 和
和 ········································································· 10分
········································································· 10分
(只写出一个点的坐标记9分)
63、(08湖南郴州28题)(本题满分10分)
如图13,在平面直角坐标系中,圆M经过原点O,且与 轴、
轴、 轴分别相交于
轴分别相交于 两点.
两点.
(1)求出直线AB的函数解析式;
(2)若有一抛物线的对称轴平行于 轴且经过点M,顶点C在⊙M上,开口向下,且经过点B,求此抛物线的函数解析式;
轴且经过点M,顶点C在⊙M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交 轴于D、E两点,在抛物线上是否存在点P,使得
轴于D、E两点,在抛物线上是否存在点P,使得 ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
(08湖南郴州28题解析)解:(1)设AB的函数表达式为
∵ ∴
∴ ∴
∴
∴直线AB的函数表达式为 .··································································· 3分
.··································································· 3分
(2)设抛物线的对称轴与⊙M相交于一点,依题意知这一点就是抛物线的顶点C。又设对称轴与 轴相交于点N,在直角三角形AOB中,
轴相交于点N,在直角三角形AOB中,
因为⊙M经过O、A、B三点,且 ⊙M的直径,∴半径MA=5,∴N为AO的中点AN=NO=4,∴MN=3∴CN=MC-MN=5-3=2,∴C点的坐标为(-4,2).
⊙M的直径,∴半径MA=5,∴N为AO的中点AN=NO=4,∴MN=3∴CN=MC-MN=5-3=2,∴C点的坐标为(-4,2).
设所求的抛物线为
则
∴所求抛物线为 ············································································· 7分
············································································· 7分
(3)令 得D、E两点的坐标为D(-6,0)、E(-2,0),所以DE=4.
得D、E两点的坐标为D(-6,0)、E(-2,0),所以DE=4.
又AC= 直角三角形的面积
直角三角形的面积
假设抛物线上存在点 .
.
当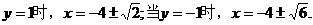 故满足条件的存在.它们是
故满足条件的存在.它们是 . ························· 10分
. ························· 10分
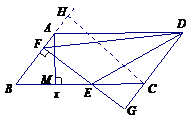
62.(08湖南郴州27题)(本题满分10分)如图10,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为 BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F. FE与DC的延长线相交于点G,连结DE,DF..
(1) 求证:ΔBEF ∽ΔCEG.
(2) 当点E在线段BC上运动时,△BEF和△CEG的周长之间有什么关系?并说明你的理由.
 (3)设BE=x,△DEF的面积为 y,请你求出y和x之间的函数关系式,并求出当x为何值时,y有最大值,最大值是多少?
(3)设BE=x,△DEF的面积为 y,请你求出y和x之间的函数关系式,并求出当x为何值时,y有最大值,最大值是多少?
(08湖南郴州27题解析)(1) 因为四边形ABCD是平行四边形, 所以 1分
1分
所以
所以 ···························································································· 3分
···························································································· 3分
(2)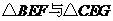 的周长之和为定值.····························································· 4分
的周长之和为定值.····························································· 4分
理由一:
过点C作FG的平行线交直线AB于H ,
因为GF⊥AB,所以四边形FHCG为矩形.所以 FH=CG,FG=CH
因此,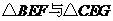 的周长之和等于BC+CH+BH
的周长之和等于BC+CH+BH
由 BC=10,AB=5,AM=4,可得CH=8,BH=6,
所以BC+CH+BH=24 ···························································································· 6分
理由二:
 由AB=5,AM=4,可知
由AB=5,AM=4,可知
在Rt△BEF与Rt△GCE中,有:
 ,
,
所以,△BEF的周长是 , △ECG的周长是
, △ECG的周长是
又BE+CE=10,因此 的周长之和是24.·········································· 6分
的周长之和是24.·········································· 6分
(3)设BE=x,则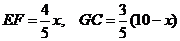
所以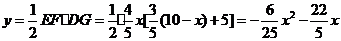 ···································· 8分
···································· 8分
配方得: .
.
所以,当 时,y有最大值.············································································· 9分
时,y有最大值.············································································· 9分
最大值为 .··········································································································· 10分
.··········································································································· 10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com