
5.设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0, ],则P到曲线y=f(x)对称轴距离的取值范围为
],则P到曲线y=f(x)对称轴距离的取值范围为
A.[0, ]
B.[0,
]
B.[0,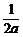 ] C.[0,|
] C.[0,|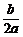 |] D.[0,|
|] D.[0,|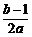 |]
|]
4.曲线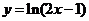 上的点到直线
上的点到直线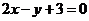 的最短距离是
( )
的最短距离是
( )

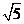
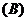
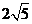


 0
0
2.下列求导运算正确的是 ( )
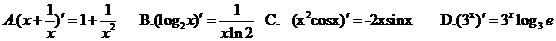 3.
3. ,
,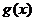 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式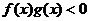 的解集是( ).
的解集是( ).
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
1.如果质点A按规律s=2t3运动,则在t=3 s时的瞬时加速度为
A.6 B.18 C.24 D.32
6.已知 ,函数
,函数 。设
。设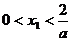 ,记曲线
,记曲线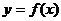 在点
在点 处的切线为
处的切线为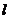 。
。
(1)求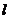 的方程;
的方程;
(2)设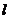 与
与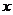 轴交点为
轴交点为 。
。
证明:①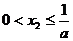 ;
;
②若 ,则
,则
[能力提升]
5.已知抛物线 ,过其上一点
,过其上一点 引抛物线的切线
引抛物线的切线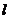 ,使
,使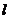 与两坐标轴在第一象限围成的三角形面积最小,求切线
与两坐标轴在第一象限围成的三角形面积最小,求切线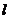 的方程.
的方程.
例6.已知抛物线 或
或 ,如果直线
,如果直线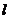 同时是
同时是 和
和 的切线,则称
的切线,则称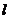 是
是 和
和 的公切线,公切线上两个切点之间的线段,称为公切线段。
的公切线,公切线上两个切点之间的线段,称为公切线段。
(1)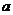 取什么值时
取什么值时 和
和 有且仅有一条公切线?写出此公切线的方程;
有且仅有一条公切线?写出此公切线的方程;
(2)若 和
和 有两条公切线,证明相应的两条公切线段互相平分。
有两条公切线,证明相应的两条公切线段互相平分。
[剖析]分别求曲线 和
和 的切线方程,由于
的切线方程,由于 和
和 有且仅有一条公切线,从而列出方程组,求解
有且仅有一条公切线,从而列出方程组,求解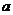 的取值,进行得到公切线方程;而对于证明相应的两条公切线段互相平分的问题,只需要证明这两条切线的中点是同一点即可.
的取值,进行得到公切线方程;而对于证明相应的两条公切线段互相平分的问题,只需要证明这两条切线的中点是同一点即可.
[解](1)函数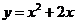 的导数是
的导数是 ,曲线
,曲线 在点
在点 处的切线方程为:
处的切线方程为: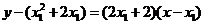 ,即
,即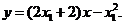 ①
①
函数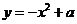 的导数是
的导数是 ,曲线
,曲线 在点
在点 处的切线方程为:
处的切线方程为:
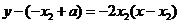 ,即
,即 ②
②
如果直线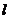 是过点
是过点 和
和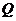 的公切线,则①②都是直线
的公切线,则①②都是直线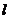 的方程,从而有
的方程,从而有
消去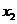 得方程
得方程 ,由
,由 ,得
,得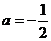 .
.
此时 ,即点
,即点 和
和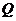 重合.故当
重合.故当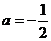 时,
时, 和
和 有且仅有一条公切线,此公切线方程为
有且仅有一条公切线,此公切线方程为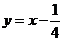 .
.
(2)由(1)知,当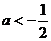 时,
时, 和
和 有两条公切线.设其中的一条公切线在
有两条公切线.设其中的一条公切线在 和
和 上的切点分别为
上的切点分别为 ,
,
则
即公切线段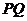 的中点是
的中点是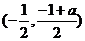
同理可证,另一条公切线段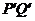 的中点也是
的中点也是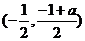 ,所以公切线段
,所以公切线段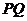 和
和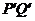 相互平分。
相互平分。
[警示]可以利用导数求曲线的切线方程,由于函数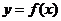 在
在 处的导数表示曲线在点
处的导数表示曲线在点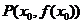 处切线的斜率,因此,曲线
处切线的斜率,因此,曲线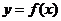 在点
在点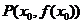 处的切线方程,可按如下方式求得:
处的切线方程,可按如下方式求得:
第一,求出函数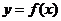 在
在 处的导数,即曲线
处的导数,即曲线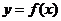 在点
在点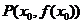 处切线的斜率;
处切线的斜率;
第二,在已知切点坐标和切线斜率的条件下,求得切线方程 ;
;
如果曲线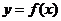 在点
在点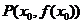 的切线平行于
的切线平行于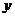 轴(此时导数不存在)时,由切线的定义可知,切线的方程为
轴(此时导数不存在)时,由切线的定义可知,切线的方程为 .
.
[变式训练]
4.已知曲线C:y=x3-3x2+2x,直线l:y=kx,且直线l与曲线C相切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标.
例5.在曲线y=x3-x上有两个点O(0,0)、A(2,6),求弧OA上点P的坐标,使△AOP的面积最大.
[剖析]本题主要考查数形结合的数学思想及导数的几何意义.由于|OA|是定值,所以若将点P的位置转化到与曲线y=x3-x相切且与OA平行的位置,此时点P到|OA|的距离最大;也可设点,构造目标函数求最值.
[解]解法一:因为kOA=3,所以过弧OA上点P的直线的斜率k′=kOA=3.
所以k′=y′=3x2-1=3.所以3x2=4. 所以x= 或x=-
或x=- (舍去).
(舍去).
所以x= ,y=
,y=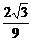 ,即P(
,即P( ,
,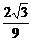 ).
).
解法二:设P(a,a3-a),∵O(0,0)、A(2,6),∴直线OA的方程为3x-y=0.
点P到它的距离为d=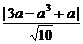 =
= |a3-4a|,
|a3-4a|,
∵0<a<2,∴4a>a3.∴d= (4a-a3).
(4a-a3).
∵(d)′= (4-3a2),令4-3a2=0,得a=
(4-3a2),令4-3a2=0,得a= 或a=-
或a=- .
.
∵0<a<2,∴x=a= 时取最大值,此时y=(
时取最大值,此时y=( )3-
)3- =
=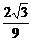 .
.
∴P( ,
,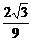 ).
).
[警示]利用导数求曲线的切线方程,几乎是新课程高考每年必考的内容,既有可能出现在选择、填空题中,也有可能出现在解答题中. 在这类问题中,导数所担负的任务是求出其切线的斜率,这类问题的核心部分是考查函数的思想方法与解析几何的基本思想。
[变式训练]
3.设 ,且
,且 ,求实数
,求实数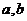 的值。
的值。
例4.已知曲线 .
.
(1)
求曲线在点 处的切线方程;
处的切线方程;
(2)求曲线过点 的切线方程。
的切线方程。
[剖析]“该曲线过点 的切线”与“该曲线在点
的切线”与“该曲线在点 处的切线方程”是有区别的:过点
处的切线方程”是有区别的:过点 的切线中,点
的切线中,点 不一定是切点;在点
不一定是切点;在点 处的切线中,点
处的切线中,点 是切点。
是切点。
[解](1)所求切线的斜率为 ,故所求的曲线的切线方程为
,故所求的曲线的切线方程为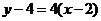 即
即
(2)设曲线 与过点
与过点 的切线相切于点
的切线相切于点 ,则切线的斜率为
,则切线的斜率为 ,切线方程为
,切线方程为 ,因为点
,因为点 在切线上,所以
在切线上,所以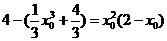 ,解得
,解得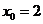 或
或 ,故所求的切线的方程为:
,故所求的切线的方程为: 或
或
[警示](1)求函数 图象上点
图象上点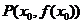 处的切线方程的关键在于确定该点切线处的斜率
处的切线方程的关键在于确定该点切线处的斜率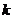 ,由导数的几何意义知
,由导数的几何意义知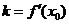 ,故当
,故当 存在时,切线方程为
存在时,切线方程为 求曲线的切线要注意“过点
求曲线的切线要注意“过点 的切线”与“点
的切线”与“点 处的切线”的差异.过点
处的切线”的差异.过点 的切线中,点
的切线中,点 不一定是切点,点
不一定是切点,点 也不一定在已知曲线上;点
也不一定在已知曲线上;点 处的切线,点
处的切线,点 是切点。
是切点。
 (2)要准确理解曲线切线的概念,①如直线与曲线公共点的个数不是切线的本质特征,一方面,直线与曲线只有一个公共点 直线是曲线的切线,例如:抛物线的对称轴与其抛物线有且仅有一个交点,但对称轴不是抛物线的切线;另一方面,直线是曲线的切线 直线与曲线有且仅有一个公共点,例如本题中曲线与其切线
(2)要准确理解曲线切线的概念,①如直线与曲线公共点的个数不是切线的本质特征,一方面,直线与曲线只有一个公共点 直线是曲线的切线,例如:抛物线的对称轴与其抛物线有且仅有一个交点,但对称轴不是抛物线的切线;另一方面,直线是曲线的切线 直线与曲线有且仅有一个公共点,例如本题中曲线与其切线 有两个公共点
有两个公共点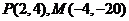 ,又如曲线
,又如曲线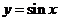 与其切线
与其切线 有无数个公共点!②曲线未必在其切线的“同侧”,例如直线
有无数个公共点!②曲线未必在其切线的“同侧”,例如直线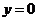 虽然“穿过”曲线
虽然“穿过”曲线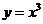 ,但它却是曲线
,但它却是曲线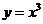 在点(0,0)处的切线。
在点(0,0)处的切线。
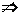 (3)要深入体会切线定义中的运动变化思想:①两个不同的公共点
(3)要深入体会切线定义中的运动变化思想:①两个不同的公共点 两公共点无限接近
两公共点无限接近 两公共点重合(切点);②割线
两公共点重合(切点);②割线 切线。
切线。
[变式训练]
2.求下列函数的导数
(1)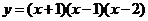 ;(2)
;(2)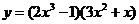 ;(3)
;(3)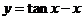 ;
(4)
;
(4)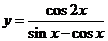 ;
(5)
;
(5)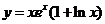 ;
(6)
;
(6)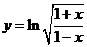
例3.已知函数 在
在 处的导数值与函数值互为相反数,求
处的导数值与函数值互为相反数,求 的值。
的值。
[剖析]可先求出函数 的导函数,然后根据条件建立关于
的导函数,然后根据条件建立关于 的方程进行求解.
的方程进行求解.
[解]由于  ,所以
,所以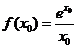 ,又
,又 ,
,
依题意得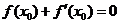 ,即
,即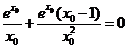 ,
, ,得
,得 。
。
[警示]
导数的运算是导数应用的前提,因步应熟练掌握导数的运算法则以及常见函数的求导公式,近几年的高考试题中,对于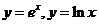 等函数导数的考查较为频繁,因此应掌握与这两个函数有关的导数运算.
等函数导数的考查较为频繁,因此应掌握与这两个函数有关的导数运算.
[变式训练]
1.(1)已知函数 在
在 处可导,且
处可导,且 ,求
,求 ;
;
(2)设 求
求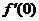 的值。
的值。
例2.求下列函数的导数
(1)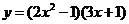 (2)
(2) (3)
(3)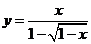
(4) (5)
(5) (6)
(6)
[剖析]本题不要考查导数的有关计算,助借于导数的计算公式及常见的初等函数的导数,可以容易求得。
[解](1) 解法一: ,
,

解法二: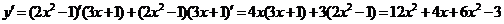
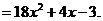
(2) 

(3) 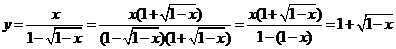 ,
,
(4) 
(5) 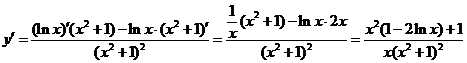 .
.
(6)

[警示]复合函数的求导过程就是对复合函数由外层逐层向里求层.每次求导都针对最外层,直到求到最里层为止.所谓最里层是指已经可以直接引用基本导数公式进行求导的.
(2)求导时,先化简再求导是运算的基本方法,这样可以减少计算量.一般说来,分式函数求导,要先观察函数的结构特征,可否化为整式函数或较为简单的分式函数;对数函数的求导,可先化为和、差的形式;三角函数的求导,先利用三角函数公式转化为和或差的形式.
[变式训练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com