

即点 总在定直线
总在定直线 上
上
[点评]本题第一问是直接待定系数求出方程,第二问本质也是求动点轨迹是一条直线采用交轨法和参数法可求解。另外第二问还可以利用直线的参数方程解题。
4、(广东卷18).(本小题满分14分)
设 ,椭圆方程为
,椭圆方程为 ,抛物线方程为
,抛物线方程为 .如图4所示,过点
.如图4所示,过点 作
作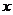 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为 ,已知抛物线在点
,已知抛物线在点 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点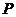 ,使得
,使得 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
 [解析](1)由
[解析](1)由 得
得 ,
,
当 得
得 ,
, G点的坐标为
G点的坐标为 ,
, ,
, ,过点G的切线方程为
,过点G的切线方程为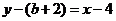 即
即 ,令
,令 得
得 ,
, 点的坐标为
点的坐标为 ,由椭圆方程得
,由椭圆方程得 点的坐标为
点的坐标为 ,
,
 即
即 ,即椭圆和抛物线的方程分别为
,即椭圆和抛物线的方程分别为 和
和 ;
;
(2) 过
过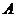 作
作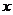 轴的垂线与抛物线只有一个交点
轴的垂线与抛物线只有一个交点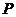 ,
, 以
以 为直角的
为直角的 只有一个,
只有一个,
同理 以
以 为直角的
为直角的 只有一个。
只有一个。
若以 为直角,设
为直角,设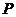 点坐标为
点坐标为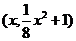 ,
,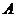 、
、 两点的坐标分别为
两点的坐标分别为 和
和 ,
,
 。
。
关于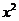 的二次方程有一大于零的解,
的二次方程有一大于零的解, 有两解,
有两解,
即以 为直角的
为直角的 有两个,
有两个,
因此抛物线上存在四个点使得 为直角三角形。
为直角三角形。
(四) 圆锥曲线
1、(08福建卷11)又曲线 (a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为(B)
(a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为(B)
A.(1,3) B.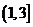 C.(3,+
C.(3,+ ) D.
) D.
[解]PF1|-|PF2|=|PF2|=2a -a,故知e≤3又因为e>1,选B
-a,故知e≤3又因为e>1,选B
[点评]圆锥曲线的几何参量是高考重点,而几何参量中的离心率又是重中之重。
[突破]解决离心率的求值或求范围问题,重要是找到 的齐次等式或不等式。
的齐次等式或不等式。
2、(08陕西卷8)双曲线 (
( ,
, )的左、右焦点分别是
)的左、右焦点分别是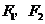 ,过
,过 作倾斜角为
作倾斜角为 的直线交双曲线右支于
的直线交双曲线右支于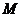 点,若
点,若 垂直于
垂直于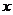 轴,则双曲线的离心率为( B )
轴,则双曲线的离心率为( B )
A. B.
B.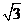 C.
C. D.
D.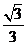
同上易知
3、(08安徽卷22).(本小题满分13分)
设椭圆 过点
过点 ,且着焦点为
,且着焦点为
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当过点 的动直线
的动直线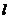 与椭圆
与椭圆 相交与两不同点
相交与两不同点 时,在线段
时,在线段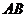 上取点
上取点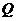 ,满足
,满足 ,证明:点
,证明:点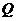 总在某定直线上
总在某定直线上
解 (1)由题意:
 ,解得
,解得 ,所求椭圆方程为
,所求椭圆方程为
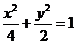
(2)方法一
设点Q、A、B的坐标分别为 。
。
由题设知 均不为零,记
均不为零,记 ,则
,则 且
且
又A,P,B,Q四点共线,从而
于是
 ,
,

 ,
, 
从而
 ,
, (1)
(1)  ,
, (2)
(2)
又点A、B在椭圆C上,即


(1)+(2)×2并结合(3),(4)得
即点 总在定直线
总在定直线 上
上
方法二
设点 ,由题设,
,由题设, 均不为零。
均不为零。
且 
又  四点共线,可设
四点共线,可设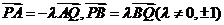 ,于是
,于是
 (1)
(1)
 (2)
(2)
由于 在椭圆C上,将(1),(2)分别代入C的方程
在椭圆C上,将(1),(2)分别代入C的方程
整理得
 (3)
(3)
 (4)
(4)
(三) 直线与圆的位置关系
1、 (2008海南、宁夏文)已知m∈R,直线l: 和圆C:
和圆C: 。
。
(1)求直线l斜率的取值范围;
(2)直线l能否将圆C分割成弧长的比值为 的两段圆弧?为什么?
的两段圆弧?为什么?
[解](Ⅰ)直线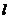 的方程可化为
的方程可化为 ,
,
直线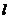 的斜率
的斜率 ,
,
因为 ,
,
所以 ,当且仅当
,当且仅当 时等号成立.
时等号成立.
所以,斜率 的取值范围是
的取值范围是 .
.
(Ⅱ)不能.
由(Ⅰ)知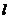 的方程为
的方程为
 ,其中
,其中 .
.
圆 的圆心为
的圆心为 ,半径
,半径 .
.
圆心 到直线
到直线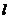 的距离
的距离
 .
.
由 ,得
,得 ,即
,即 .从而,若
.从而,若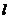 与圆
与圆 相交,则圆
相交,则圆 截直线
截直线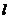 所得的弦所对的圆心角小于
所得的弦所对的圆心角小于 .
.
所以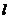 不能将圆
不能将圆 分割成弧长的比值为
分割成弧长的比值为 的两段弧.
的两段弧.
[点评]此题考查了直线方程,函数求值域,直线与圆的位置关系。难度不大但很好的综合了以上知识点。
[突破]注意把直线方程中的 换成k使表达简单,减小运算量。
换成k使表达简单,减小运算量。
(二)圆
1、 (2008上海文、理)如图,在平面直角坐标系中,
(2008上海文、理)如图,在平面直角坐标系中, 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成的区域(含边界),A、B、C、D是该圆的四等分点.若点
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成的区域(含边界),A、B、C、D是该圆的四等分点.若点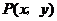 、点
、点 满足
满足 且
且 ,则称P优于
,则称P优于 .如果
.如果 中的点
中的点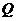 满足:
满足:
不存在 中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( D )
中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( D )
A. B. C. D.
[解]由题意可知Q点一定是圆上的一段弧且纵坐标较大横坐标较小,
故知是上半圆的左半弧。
[点评]此题是一个情景创设题,考查学生的应变能力。
[突破]Q点的纵坐标较大,横坐标较小。
2、(2008天津文)已知圆 的圆心与点
的圆心与点 关于直线
关于直线 对称.直线
对称.直线 与圆
与圆 相交于
相交于 两点,且
两点,且 ,则圆
,则圆 的方程为
的方程为 
[解]利用圆的标准方程待定系数易得结果。
[点评]此题虽小但考查到了对称、直线与圆相交、圆的方程等知识。
[突破]利用对称求出圆心坐标,利用直角三角形解出半径。
(一)直线
1、(2008四川文、理) 直线 绕原点逆时针旋转
绕原点逆时针旋转 ,再向右平移1个单位,所得到的直线为( A )
,再向右平移1个单位,所得到的直线为( A )
(A) (B)
(B) (C)
(C) (D)
(D)
[解]∵直线 绕原点逆时针旋转
绕原点逆时针旋转 的直线为
的直线为 ,从而淘汰(C),(D)
,从而淘汰(C),(D)
又∵将 向右平移1个单位得
向右平移1个单位得 ,即
,即 故选A;
故选A;
[点评]此题重点考察互相垂直的直线关系,以及直线平移问题;
[突破]熟悉互相垂直的直线斜率互为负倒数,过原点的直线无常数项;重视平移方法:“左加右减”;
2、 (2008江苏) 如图,在平面直角坐标系
(2008江苏) 如图,在平面直角坐标系 中,设三角形
中,设三角形 的顶点分别为
的顶点分别为 ,点
,点 在线段AO上的一点(异于端点),这里
在线段AO上的一点(异于端点),这里 均为非零实数,设直线
均为非零实数,设直线 分别与边
分别与边 交于点
交于点 ,某同学已正确求得直线
,某同学已正确求得直线 的方程为
的方程为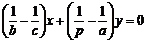 ,请你完成直线
,请你完成直线 的方程: (
的方程: (  )
) 。
。
[解]画草图,由对称性可猜想填 .事实上,由截距式可得直线AB:
.事实上,由截距式可得直线AB: ,直线CP:
,直线CP: ,两式相减得
,两式相减得 ,显然直线AB与CP 的交点F 满足此方程,又原点O 也满足此方程,故为所求直线OF 的方程.[答案]
,显然直线AB与CP 的交点F 满足此方程,又原点O 也满足此方程,故为所求直线OF 的方程.[答案]
[点评]本小题考查直线方程的求法.
[突破]注意观察出对称性。
(三)高频考点及考题类型
1、直线以倾斜角、斜率、夹角、距离、平行与垂直、线性规划(老)等有关的问题,其中要重视“对称问题”及”线性规划问题”的解答。
2、与圆位置有关的问题,一是研究方程组;二是充分利用平面几何知识。重在后者。
3、求曲线的方程或轨迹问题,涉及圆锥曲线的定义和几何性质(如求离心率的问题)
4、直线与圆锥曲线的位置关系问题,如参数的变量取值范围、最值;几何参量的求值问题。
5、以圆锥曲线为载体在知识网络的交汇点设计问题,其目的是加强联系注重应用,考查学生的应变能力以及分析问题和解决问题的能力。
(一)基本知识网络
 (二)基本知识点(定义公式)
(二)基本知识点(定义公式)
1、 直线
(1)两点P1(x1,y1)、P2(x2,y2)的距离公式: .
.
若直线 的斜率为k,则
的斜率为k,则 .
.
(老教材)定比分点坐标分式。若点P(x,y)分有向线段 ,其中P1(x1,y1),P2(x2,y2).则
,其中P1(x1,y1),P2(x2,y2).则

特例,中点坐标公式;重要结论,三角形重心坐标公式。
(2) 直线的倾斜角(0°≤ <180°)、斜率:
<180°)、斜率: 过两点
过两点 .
. 
当 (即直线和x轴垂直)时,直线的倾斜角
(即直线和x轴垂直)时,直线的倾斜角 =
= ,没有斜率
,没有斜率
(3)直线方程的几种形式:
|
直线名称 |
已知条件 |
直线方程 |
使用范围 |
|
点斜式 |
 |
 |
k存在 |
|
斜截式 |
k,b |
 |
k存在 |
|
两点式 |
(x1,y1)、(x2,y2) |
 |
 |
|
截距式 |
a,b |
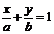 |
 |
|
一般式 |
|
 |
A、B不全为0 |
|
参数式 |
倾斜角 |
 |
t为参数 |
(4)两条直线的位置关系
①若两条直线的方程分别为 l1: y=k1x+b1; l2: y=k2x+b2.则
l1|| l2⇔k1=k2,且b1≠b2; l1⊥l2⇔k1•k2= -1 ;
当1+k1k2≠0时,若q为l1到l2的角,则 , 若α为l1和l2的夹角则
, 若α为l1和l2的夹角则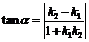 ,
,
②如果直线l1、l2的方程分别为l1:A1x+B1y+C1=0, l2: A2x+B2y+C2=0 则l1与l2
相交的充要条件: ;交点坐标:
;交点坐标:
. 平行的充要条件:l1|| l2⇔A1B2-A2B1=0,(B1C2-B2C1)2+(C1A2-C2A1)2≠0.
垂直的充要条件:l1⊥ l2⇔A1A2+B1B2=0.
重合的充要条件:l1与l2重合⇔A1B2-A2B1=B1C2-B2C1=C1A2-C2A1=0 (或 ).
).
若 A1A2+B1B2≠0,直线l1到直线l2的角是θ,则有tanθ=
(5)直线系方程
①与直线:Ax+By+C= 0平行的直线系方程是:Ax+By+m=0.( m∊R, C≠m).
② 与直线:Ax+By+C= 0垂直的直线系方程是:Bx-Ay+m=0.( m∊R)
③ 过定点(x1,y1)的直线系方程是: A(x-x1)+B(y-y1)=0 (A,B不全为0)
④ 过直线l1、l2交点的直线系方程:(A1x+B1y+C1)+λ( A2x+B2y+C2)=0 (λ∊R) 注:该直线系不含l2.
(5)距离
①点P(xo,yo)到直线l:Ax+By+C=
0的距离

②两平行线l1:Ax+By+c1=0, l2:Ax+By+c2=0间的距离公式:d=
2、圆
(1) 圆的定义:平面上到一定点的距离等于定长的点的轨迹。
(2) 圆的方程
① 圆的标准方程:(x-a)2+(y-b)2=r2
②一般方程:x2+y2+Dx+Ey+F=0,(D2+E2-4F>0) 圆心坐标:(- ,-
,- ) 半径r=
) 半径r=

③以(x1,y1),(x2,y2)为直径两端的圆的方程:(x-x1)(x-x2)+(y-y1)(y-y2)=0
④圆的参数方程: (
( 为参数)
为参数)
(3) 点与圆的位置关系
设圆C∶(x-a)2+(y-b)2=r2,点M(x0,y0)到圆心的距离为d,则有:
几何表示(1)d>r  点M在圆外; (2)d=r
点M在圆外; (2)d=r  点M在圆上;
(3)d<r
点M在圆上;
(3)d<r  点M在圆内.
点M在圆内.
代数表示(x -a)2+(y
-a)2+(y -b)2>r2
-b)2>r2 点M在圆外;(x
点M在圆外;(x -a)2+(y
-a)2+(y -b)2=r2
-b)2=r2 点M在圆上;(x
点M在圆上;(x -a)2+(y
-a)2+(y -b)2<r2
-b)2<r2 点M在圆内;
点M在圆内;
(4)直线与圆的位置关系
设圆C:(x-a)2+(y-b)2=r2, 直线l的方程为Ax+By+C=0.1圆心(a,b)到l的距离为d;
2 消去y得关于x的一元二次方程判别式为△,则有:
消去y得关于x的一元二次方程判别式为△,则有:
|
位置关系 |
公共点个数 |
数量关系 |
|
|
相离 |
0 |
d>r |
⊿< 0 |
|
相切 |
1 |
d=r |
⊿ = 0 |
|
相交 |
2 |
d<r |
⊿> 0 |
(5) 圆与圆的位置关系
设圆C1:(x-a)2+(y-b)2=r12和圆C2:(x-m)2+(y-n)2=r22(r1≥r2),且设两圆圆心距为d,则有:
|
位置关系 |
相离 |
外切 |
相交 |
内切 |
内含 |
|
数量关系 |
d> r1+r2 |
d=r1+r2 |
r1-r2<d<r1+r2 |
d=r1-r2 |
d<r1-r2(d=0:两圆同心) |
(6)几个常用结论和方法
①弦长的求解:弦心距d、圆半径r、弦长l,则: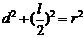 (根据垂弦定理和勾股定理)
(根据垂弦定理和勾股定理)
②圆的切线方程的求法
过圆上的点的圆的切线方程
..圆x2+y2=r2,圆上一点为(x0,y0),则此点的切线方程为x0x+y0y=r2(课本命题).
..圆(x-a)2+(y-b)2=r2,圆上一点为(x0,y0),则过此点的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2(课本命题的推广).
..以(x0,y0)为切点的圆x2+y2+Dx+Ey+F=0的切线方程:分别以xox,yoy, 替换圆方程中的x2,y2,x,y.
替换圆方程中的x2,y2,x,y.
过圆外一点M(xo,yo),作圆(x-a)2+(y-b)2=r2的切线,可设切线方程为点斜式:
y-yo=k(x-xo),利用圆心到直线的距离等于半径或与圆的方程联立用判别式法求k。
注意: 由圆外一点向圆引切线,应当有两条切线。但,可能只算出一个 k值,那么,另一条斜率不存在,即过(x0,y0)垂直于x轴的直线x=x0.
③两圆相交时的公共弦方程、两圆外切时的内公切线、两圆内切时的外公切线:两圆方程作差,消去二次项所得的直线方程即为所求。
3圆锥曲线
(1)椭圆、双曲线、抛物线的标准方程与几何性质(见后表)
(2)椭圆、双曲线、抛物线的标准方程的其他形式及相应性质.
(3)等轴双曲线
(4)共轭双曲线
(5)方程y2=ax与x2=ay的焦点坐标及准线方程.
(6)共渐近线的双曲线系方程.
(7)点、直线与圆锥曲线的位置关系
椭圆、双曲线、抛物线的标准方程与几何性质
|
|
椭圆 |
双曲线 |
抛物线 |
|
|
定义 |
1.到两定点F1,F2的距离之和为定值2a(2a>|F1F2|)的点的轨迹 |
1.到两定点F1,F2的距离之差的绝对值为定值2a(0<2a<|F1F2|)的点的轨迹 |
|
|
|
2.与定点和直线的距离之比为定值e的点的轨迹.(0<e<1) |
2.与定点和直线的距离之比为定值e的点的轨迹.(e>1) |
与定点和直线的距离相等的点的轨迹. |
||
|
图形 |
|
|
|
|
|
方 程 |
标准方程 |
 ( ( >0) >0) |
 (a>0,b>0) (a>0,b>0) |
y2=2px |
|
参数方程 |
 |
 |
 (t为参数) (t为参数) |
|
|
范围 |
─a£x£a,─b£y£b |
|x| ³ a,yÎR |
x³0 |
|
|
中心 |
原点O(0,0) |
原点O(0,0) |
|
|
|
顶点 |
(a,0), (─a,0), (0,b) , (0,─b) |
(a,0), (─a,0) |
(0,0) |
|
|
对称轴 |
x轴,y轴; 长轴长2a,短轴长2b |
x轴,y轴; 实轴长2a, 虚轴长2b. |
x轴 |
|
|
焦点 |
F1(c,0),
F2(─c,0) |
F1(c,0),
F2(─c,0) |
 |
|
|
焦距 |
2c (c= ) ) |
2c (c= ) ) |
|
|
|
离心率 |
    |
 |
e=1 |
|
|
准线 |
x= |
x= |
 |
|
|
渐近线 |
|
y=± x x |
|
|
|
焦半径 |
 |
 |
 |
|
|
通径 |
 |
 |
2p |
|
|
焦参数 |
 |
 |
P |
4、曲线和方程
1.曲线与方程:在直角坐标系中,如果曲线C和方程f(x,y)=0的实数解建立了如下的关系:
(1) 曲线C上的点的坐标都是方程f(x,y)=0的解(纯粹性);
(2) 方程f(x,y)=0的解为坐标的点都在曲线C上(完备性)。
则称方程f(x,y)=0为曲线C的方程,曲线C叫做方程f(x,y)=0的曲线。
2.求曲线方程的方法:.
(1)待定系数法; (2) 直接法(直译法);(3)定义法; (4)相关点代入法(转移法);(5)参数法.
3.过两条曲线f1(x,y)=0与f2(x,y)=0的公共点的曲线系方程:
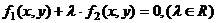
(二)考点预测题
1. (广东省实验中学2008年高三第三次模拟考试,数学理科,1)如图所示的韦恩图中,A,B 是非空集合,定义集合A#B为阴影部分表示的集合.若x,y∈R,A={x|y=
(广东省实验中学2008年高三第三次模拟考试,数学理科,1)如图所示的韦恩图中,A,B 是非空集合,定义集合A#B为阴影部分表示的集合.若x,y∈R,A={x|y= },B={y|y=3x,x>0},则A#B=( )
},B={y|y=3x,x>0},则A#B=( )
A {x|0<x<2} B {x|1<x≤2} C {x|0≤x≤1或x≥2} D {x|0≤x≤1或x>2}
[解析]
[答案]D
2.(福建省泉州一中高2008届第一次模拟检测,数学理科,1)()集合 ,则
,则 ( )
( )
A. B.
B. C.
C. D.
D.
[解析]
[答案]C
3.(广东省惠州市2008届高三第三次调研考试,数学理科,1)设集合 ,则满足
,则满足 的集合B的个数是( ).
的集合B的个数是( ).
A.1 B.3 C.4 D.8
[解析] ,
, ,则集合B中必含有元素3,即此题可转化为求集合
,则集合B中必含有元素3,即此题可转化为求集合 的子集个数问题,所以满足题目条件的集合B共有
的子集个数问题,所以满足题目条件的集合B共有 个。
个。
[答案]C
本资料由《七彩教育网》 提供!
(一)文字介绍
本部分是高考每年必考内容,考试多以选择填空的形式出现,而且通常只考一题,属于简单题,09高考这种模式应该不会改变,仍将以一道小题考查。主要考查集合的运算及相关知识。
7.(江苏省启东中学2008届高三综合测试二,数学,1)定义集合A*B={x|xA,且x B},若A={1,3,5,7},B={2,3,5},则A*B的子集个数为( )
B},若A={1,3,5,7},B={2,3,5},则A*B的子集个数为( )
A.1 B.2 C.3 D.4
[解析]本题考查子集的个数问题,A*B={1, 7},A*B的子集个数为
[答案]D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com