
2、高考命题趋势
(1)高考题型:选择与填空。
(2)难易程度:以中档题为主,基础题为辅。
(3)高频考点:循环结构的程序框图。说明:安徽09高考不会考到算法语言,因为皖南,皖北选用了不同版本教材,算法语言编写不同,答卷时学生会有地域性差别,造成教师改卷有感情因素,影响公正。
07、08两年新课改地区加上上海程序框图共考了11题,有9题考查了循环结构,只有08年海南、宁夏考了条件结构,07上海有语言考查。且大部分题都是与数列结合。(可见安徽09也应如此,求稳)
1、试题特点
(1)前两年考试情况简介
算法初步是新课标教材的新增内容,2007开始第一年高考,到2009年是第三年了,前两年在新课改地区如广东、宁夏、海南、山东都出现了算法初步的问题,但都以小题呈现且都考查的是程序框图。
(2)试题特点
显示一:考小题,考程序框图
近两年高考中算法都考了程序框图,一个小题选择或填空--5分。
显示二:考框图,考循环结构
(二)考点预测题
1.(广东省湛江一中08-09高三理科数学月考试卷2009.2,数学,8)已知 为直线,
为直线,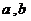 为平面,给出下列命题:
为平面,给出下列命题:
① ②
② ③
③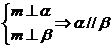 ④
④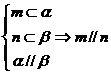
其中的正确命题序号是:
A ③④ B ②③ C ①② D ①②③④
[解析]本题考查位置关系的判定,属于简单题
[答案] B
2.(江苏省盐城中学2008年高三上学期第二次调研测试题,数学,8)如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其左视图的面积为 。

[解析]本题考查三视图几面积的计算,先画出左视图,再进行求解,左视图如上图,故所求面积为
[答案]
3.(山东省烟台市2008-2009学年高三年级模块检测,数学文科,19) 如图,已知三棱
锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形。
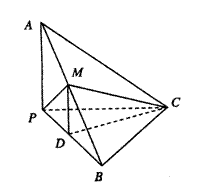 (1)求证:DM∥平面APC;
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积。
[解析]本题考查线面平行的证明,面面垂直的证明以及三棱锥体积的计算
[答案](1)∵M为AB中点,D为PB中点,
∴MD//AP,
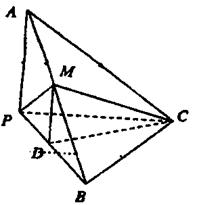
又∴MD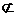 平面ABC
平面ABC
∴DM//平面APC。
(2)∵△PMB为正三角形,且D为PB中点。
∴MD⊥PB。
又由(1)∴知MD//AP, ∴AP⊥PB。
 又已知AP⊥PC ∴AP⊥平面PBC,
又已知AP⊥PC ∴AP⊥平面PBC,
∴AP⊥BC, 又∵AC⊥BC。
∴BC⊥平面APC,
∴平面ABC⊥平面PAC,
(3)∵AB=20
∴MB=10 ∴PB=10
又BC=4,
∴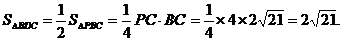
又MD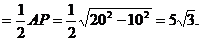
∴VD-BCM=VM-BCD=
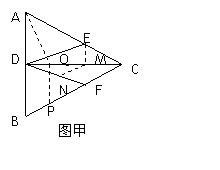
4.(沈阳二中2009届高三期末数学试题,数学理科,18)如图甲正三角形ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,先将△ABC沿CD折叠成直二面角A-DC-B(如图乙),在乙图中
(Ⅰ)求二面角E-DF-C的余弦值;
(Ⅱ)在线段BC上找一点P,使AP⊥DE,并求BP.
(Ⅲ)求三棱锥D-ABC外接球的表面积.(只需用数字回答,可不写过程)
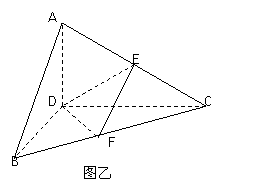
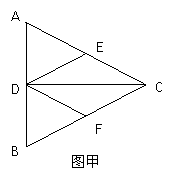
[解析]本题考查翻折几何体的相关问题,并计算二面角的大小,以及有关点的位置的探究和球的体积计算
[答案](1)∵AD⊥CD,BD⊥CD,∴∠ADB是二面角A-CD-B的平角
∴ AD⊥BD ∴AD⊥平面BCD,取CD的中点M,这时EM∥AD,∴EM⊥平面BCD
过M作MN⊥DF于点N,连结EN,则EN⊥DF
∴∠MNE是二面角E-DF-N的平面角
在 Rt△EMN中,EM= AD=
AD= AB=1,MN=
AB=1,MN=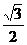 ∴EN=
∴EN= ,cos∠MNE=
,cos∠MNE=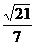

(2) 在线段BC上取点P,使BP= BC=
BC=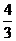 ,
,
过P作PQ⊥CD于点Q,
∴ PQ⊥平面ACD
∵DQ= DC=
DC= ,在等边△ADE中,∠DAQ=30
,在等边△ADE中,∠DAQ=30
∴AQ⊥DE,∴AP⊥DE
(3) 2R=
(一)文字介绍
立体几何每年高考必考,一般为一小一大,小题多考位置关系的简单的概念性判断,和三视图以及面积体积,尤其三视图是新课标的新增内容,在高考中将成为命题的热点,解答题多以证明位置关系,计算角与距离为为,文科侧重于证明,理科要学会用空间向量解决相应问题。
7.(浙江省余姚中学08-09学年上学期高三第三次质量检测,数学理科,19)如图,四棱锥P-ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
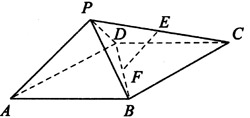 (2)证明:面PDC⊥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求锐二面角B-PD-C的余弦值.
[解析]本题考查线面平行及面面垂直的证明,并计算二面角
[答案]证明:(1)如图,连接AC,∵ABCD为矩形且F是BD的中点,
∴AC必经过F
又E是PC的中点,
所以,EF∥AP
∵EF在面PAD外,PA在面内,∴EF∥面PAD
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD 面ABCD=AD,∴CD⊥面PAD,
面ABCD=AD,∴CD⊥面PAD,
又AP 面PAD,∴AP⊥CD
面PAD,∴AP⊥CD
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD
又AD 面PAD,所以,面PDC⊥面PAD
面PAD,所以,面PDC⊥面PAD
(3)由P作PO⊥AD于O,以OA为x轴,以OF为y轴,以OP为z轴,则
A(1,0,0),P(0,0,1)
由(2)知 是面PCD的法向量,B(1,1,0),D(一1,0,0),
是面PCD的法向量,B(1,1,0),D(一1,0,0),
 ,
,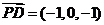
设面BPD的法向量 ,
,
由 得
得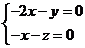
取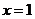 ,则
,则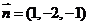 ,
,
向量 和
和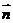 的夹角的余弦
的夹角的余弦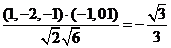
所以,锐二面角B-PD-C的余弦值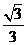
6.(山东省烟台市2008年高三适应性练习(三),数学理科,19)如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中 点。
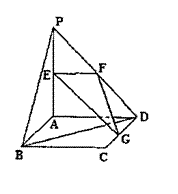 (1)求证:PB//平面EFG;
(1)求证:PB//平面EFG;
(2)求异面直线EG与BD所成的角的余弦值;
(3)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离为 ,若存在,求出CQ的值;若不存在,请说明理由。
,若存在,求出CQ的值;若不存在,请说明理由。
[解析]本题考查线面平行的证明,和异面直线所成角的求法,及点面距离的求解,理科生应学会利用空间向量解决问题。
[答案]解法一:(1)证明:取AB为中点H,连结GH,HE,
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH//AD//EF,
∴E,F,G,H四点共面。
又H为AB中点,
∴EH//PB。
又EH 面EFG,PB
面EFG,PB 平面EFG,
平面EFG,
∴PB//面EFG。
(2)解:取BC的中点M,连结GM、AM、EM,则GM//BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角。
在Rt△MAE中,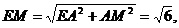
同理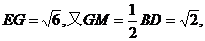
∴在Rt△MGE中,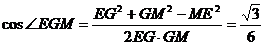
故异面直线EG与BD所成角的余弦值为
(3)假设在线段CD上存在一点Q,满足题设条件,过点Q作OR⊥AB于R,连结RE,则QR//AD。
 ∵ABCD是正方形,△PAD是直角三角形
,且PA=AD=2,
∵ABCD是正方形,△PAD是直角三角形
,且PA=AD=2,
∴AD⊥AB,AD⊥PA
又AB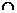 PA=A,
PA=A,
∴AD⊥平面PAB。
又∵E,F分别是PA,PD中点,
∴EF//AD,
∴EF⊥平面PAB
又EF 面EFQ,
面EFQ,
∴EFQ⊥平面PAB。
过A作AT⊥ER于T,则AT⊥面EFQ,
∴AT就是点A到平面EFQ的距离。
设
在Rt△EAR中,AT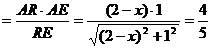
解得 。
。
故存在点Q,当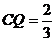 时,点A到平面EFQ的距离为
时,点A到平面EFQ的距离为
解法二:建立如图所示的空间直角坐标系A-xyz,
则A(0,0,0),B(2,0,0,),C(2,2,0),
 D(0,2,0)P(0,0,2),E(0,0,1),
D(0,2,0)P(0,0,2),E(0,0,1),
F(0,1,1),G(1,2,0)。
(1)证明:∵

设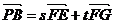
即(2,0,-2)=S(0,-1,0)+t(1,1,-1)
解得s=t=2
∴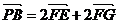
又∵
∴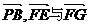 共面。
共面。
∵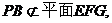
∴PB//平面EFG。
(2)解∵
∴
故平面直线EG与BD所成角的余弦值为
(3)假设在线段CD上存在一点Q满足题设条件。
令 ,则DQ=2-m
,则DQ=2-m
∴点Q的坐标为(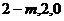 )
)
∴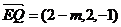
而 ,则
,则
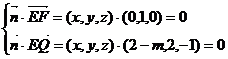
∴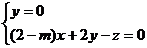
令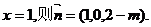
又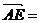 (0,0,1)
(0,0,1)
∴点A到平面EFQ的距离
即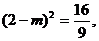
∴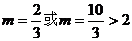 不合题意,舍去。
不合题意,舍去。
故存在点Q,当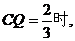 点A到平面EFQ的距离为
点A到平面EFQ的距离为
5.(南通四县市2008届高三联合考试,数学,17)如图,在长方体ABCD-A1B1C1D1中,AB= AD=2.
(1)证明:面BDD1 B1⊥面ACD1;
(2)若E是BC1的中点,P是AC的中点,F是A1C1上的点, C1F=mFA1,试求m的值,使得EF∥D1P.
[解析]本题考查面面垂直的证明,以及线线垂直的探究
[答案]证明(1):在长方体ABCD-A1B1C1D1中,AB= AD=2,
 故四边形ABCD是正方形,AP⊥DP,
故四边形ABCD是正方形,AP⊥DP,
又∵D1D⊥面ABCD,AP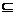 面ABCD
面ABCD
∴D1D⊥AP ,D1D∩DP=D
∴AP⊥面BDD1B1
∵AP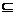 面AD1C
面AD1C
∴面BDB1D1⊥面ACD1
(2):记A1C1与B1D1的交点为Q,连BQ,
∵P是AC的中点,∴D1P∥BQ,要使得EF∥D1P,则必有EF∥BQ
在△QBC1中,E是BC1的中点, F是QC1上的点,EF∥BQ
∴F是QC1的中点,即3C1F=FA1,故所求m的值是 .
.
4.(广东省中山市2009年四校联考数学,数学理科,5)给出下列关于互不相同的直线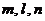 和平面
和平面 的四个命题:
的四个命题:
①若 ;
;
②若 是异面直线,
是异面直线,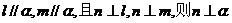 ;
;
③若 ;
;
④若
其中为假命题的是 ( )
A.① B.② C.③ D.④
[解析]本题考查线线,线面及面面位置关系的判定
[答案]C
3. (山东省潍坊市2008年5月高三教学质量检测,数学理科,12)如图,ABCD中,AB⊥BD,沿BD将△ABD折起,使面ABD⊥面BCD,连结AC,则在四面体ABCD的四个面中,互相垂直的平面有( )对
(山东省潍坊市2008年5月高三教学质量检测,数学理科,12)如图,ABCD中,AB⊥BD,沿BD将△ABD折起,使面ABD⊥面BCD,连结AC,则在四面体ABCD的四个面中,互相垂直的平面有( )对
A.1 B.2
C.3 D.4
[解析]本题考查图形的翻折,和面面垂直的判定,显然面ABD⊥面BCD,面ABC⊥面BCD,面ABD⊥面ACD,
[答案]C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com