
1.在复习不等式的解法时,要加强等价转化思想的训练,以便快速、准确求解.在解或证明含有参数不等式的过程中,一般要对参数进行分类讨论,因此,还要加强分类讨论思想的训练,做到分类合理、不重不漏.由于不等式、函数、方程三者密不可分,相互联系、互相转化,所以,强化函数与方程思想在不等式中的应用训练十分必要.
(四)高考对不等式的考查侧重以下几个方面:
1.不等式性质的考查常与幂函数、指数函数和对数函数的性质的考查结合起来,一般多以选择题的形式出现,有时与充要条件的知识联系在一起.解答此类题目要求考生要有较好、较全面的基础知识,一般难度不大.
2.高考试卷中,单纯不等式的考题,一般是中档难度题,内容多涉及不等式的性质和解法,以及重要不等式的应用.解不等式的考题常以填空题和解答题的形式出现.在解答题中,含字母参数的不等式问题较多,需要对字母参数进行分类讨论,这类考题多出现在文科试卷上.
3.证明不等式近年来逐渐淡化,但若考试卷中出现不等式证明,则往往不是单独的纯不等式证明,而是与函数、三角、解析几何、数列、导数等知识综合考查,这时有可能是压轴题或倒数第二题.此类考题区分度高,综合性强,与同学们平时联系的差距较大,考生要有较强的逻辑思维能力和较高的数学素质才能取得较好的成绩.这类考题往往是理科试卷中经常出现的题型.
4.应用问题是近年数学高考命题的热点,近些年高考试题带动了一大批“以实际问题为背景,以函数模型,以重要不等式为解题工具”的应用题问世.解此类考题在合理地建立不等关系后,判别式、重要不等式是常用的解题工具.
5.含有绝对值的不等式经常出现在高考试卷中,有关内容在教材中安排较少,考生解此类问题大多感觉困难,这与平时练习量不足有关,对此应有所加强.
6.解不等式的基本思想是转化,解题思路是利用不等式的性质及结合有关函数的性质把问题转化为一元一次不等式、一元二次不等式、含有基本初等函数的最基本不等式,然后求解.在这里着重强调的是,解不等式是在不等式有意义的前提下求出满足不等式的未知数取值的集合,在解无理不等式、对数不等式时,要注意其定义域.
(三)高考考纲对不等式的要求:
(1)理解不等式的性质及其证明;(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理及其变形,并会简单的应用;(3)掌握分析法、综合法、比较法证明简单的不等式;切实掌握上述三种方法证明不等式的方法步骤及使用范围,提高数学式的变形能力;(4)掌握简单不等式的解法;掌握含参数不等式的解法及它在函数等方面的应用;(5)理解不等式|a|-|b|≤|a+b|≤|a|+|b|.对不等式重点考查的有四种题型:解不等式、证明不等式、不等式的应用、不等式的综合.
(二)不等式知识要点
1.不等式的基本概念
不等(等)号的定义:
不等式的分类:绝对不等式;条件不等式;矛盾不等式.
同向不等式与异向不等式.
同解不等式与不等式的同解变形.
2.不等式的基本性质
(1) (对称性)
(对称性)
(2) (传递性)
(传递性)
(3) (加法单调性)
(加法单调性)
(4) (同向不等式相加)
(同向不等式相加)
(5) (异向不等式相减)
(异向不等式相减)
(6)
(7) (乘法单调性)
(乘法单调性)
(8) (同向不等式相乘)
(同向不等式相乘)
 (异向不等式相除)
(异向不等式相除)
 (倒数关系)
(倒数关系)
(11) (平方法则)
(平方法则)
(12) (开方法则)
(开方法则)
3.几个重要不等式
(1)
(2) (当仅当a=b时取等号)
(当仅当a=b时取等号)
(3)如果a,b都是正数,那么
 (当仅当a=b时取等号)
(当仅当a=b时取等号)
极值定理:若 则:
则:
1如果P是定值,那么当x=y时,S的值最小;
2如果S是定值,那么当x=y时,P的值最大.
利用极值定理求最值的必要条件: 一正、二定、三相等.
 (当仅当a=b=c时取等号)
(当仅当a=b=c时取等号)
 (当仅当a=b时取等号)
(当仅当a=b时取等号)

(7)
4.几个著名不等式
(1)平均不等式: 如果a,b都是正数,那么
 (当仅当a=b时取等号)即:平方平均≥算术平均≥几何平均≥调和平均(a、b为正数):特别地,
(当仅当a=b时取等号)即:平方平均≥算术平均≥几何平均≥调和平均(a、b为正数):特别地, (当a = b时,
(当a = b时, )
)

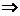 幂平均不等式:
幂平均不等式:
注:例如: .
.
常用不等式的放缩法:①
②
(2)柯西不等式: 
(3)琴生不等式(特例)与凸函数、凹函数
若定义在某区间上的函数f(x),对于定义域中任意两点 有
有
 则称f(x)为凸(或凹)函数.
则称f(x)为凸(或凹)函数.
5.不等式证明的几种常用方法
比较法、综合法、分析法、换元法、反证法、放缩法、构造法.
6.不等式的解法
(1)整式不等式的解法(根轴法).
步骤:正化,求根,标轴,穿线(偶重根打结),定解.
特例① 一元一次不等式ax>b解的讨论;②一元二次不等式ax2+bx+c>0(a≠0)解的讨论.
(2)分式不等式的解法:先移项通分标准化,则

(3)无不等理式:转化为有理不等式求解
1
2 3
3
(4)指数不等式:转化为代数不等式

(5)对数不等式:转化为代数不等式

(6)含绝对值不等式
应用分类讨论思想去绝对值;应用数形思想;应用化归思想等价转化.

注:常用不等式的解法举例(x为正数):
①
②
类似于 ,③
,③
(一) 考试内容:
不等式的基本性质;不等式的证明;不等式的解法;含绝对值的不等式.
(二)考点预测题
1.(2008年山东卷,数学理科,4)设函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a的值为
(A) 3 (B)2 (C)1 (D)-1
[解析]本题考查函数的性质,函数的性质是重点考查内容,对函数的几个性质应熟练掌握,09高考必将有涉及函数性质的题目出现, 、
、 在数轴上表示点
在数轴上表示点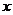 到点
到点 、
、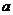 的距离,他们的和
的距离,他们的和 关于
关于 对称,因此点
对称,因此点 、
、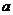 关于
关于 对称,所以
对称,所以 (直接去绝对值化成分段函数求解比较麻烦,如取特殊值解也可以)
(直接去绝对值化成分段函数求解比较麻烦,如取特殊值解也可以)
[答案]A
2.(2008年上海卷,数学文科,9)若函数 (常数
(常数 )是偶函数,且它的值域为
)是偶函数,且它的值域为 ,则该函数的解析式
,则该函数的解析式 .
.
[解析]本题考查函数的解析式, 是偶函数,则其图象关于y轴对称,
是偶函数,则其图象关于y轴对称, 
 且值域为
且值域为 ,
, 

[答案]
3.(2008年广东卷,数学理科,19)设 ,函数
,函数 ,
, ,
, ,试讨论函数
,试讨论函数 的单调性.
的单调性.
[解析]本题考查函数的综合应用,广东连续两年均考查了函数解答题,江苏08年也以函数作为压轴题,应引起一定重视。
[答案]

对于 ,
,
当 时,函数
时,函数 在
在 上是增函数;
上是增函数;
当 时,函数
时,函数 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
对于 ,
,
当 时,函数
时,函数 在
在 上是减函数;
上是减函数;
当 时,函数
时,函数 在
在 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。
(一)文字介绍
本节内容在高考中占有一定比重,而且二分法是新增内容,应引起重视,同时对反函数的考查要求降低,本节多数题目将会以小题目出现,重点仍将是考查函数的性质,二分法,函数的定义域,以及函数的综合应用等知识点。
6. (山东省济宁市2009届高三11月教学质量检测,数学理科,20)函数
(山东省济宁市2009届高三11月教学质量检测,数学理科,20)函数 和
和 的图象的示意图如图4所示,设两函数的图象交于点
的图象的示意图如图4所示,设两函数的图象交于点 ,且
,且
(1)请指出示意图中 分别对应哪一个函数?
分别对应哪一个函数?
(2)若 ,
,
且 ,指出a,b的值,并说明理由;
,指出a,b的值,并说明理由;
(3)结合函数图象的示意图,判断

 的大小,并按从小到大的顺序排列。
的大小,并按从小到大的顺序排列。
[解析]考查函数的综合运用
[答案](1) 对应的函数为
对应的函数为 ,
, 对应的函数为
对应的函数为
(2)
理由如下:
令 ,则
,则 为函数
为函数 的零点。
的零点。
 ,
,
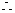 方程
方程 的两个零点
的两个零点
因此整数
(3)从图像上可以看出,当 时,
时,
当 时,
时,

5.(安徽省六校2009年高三联考试卷,数学文科,11)己知 是偶函数,当
是偶函数,当 时,
时, ,且当
,且当 时
时 恒成立,则
恒成立,则 的最小值是( )
的最小值是( )
A  B
B  C 1
D
C 1
D 
[解析]本题考查函数的性质及函数在给定区间上的最值,当 时,
时, ,故
,故 恒成立,则
恒成立,则 的最小值是1
的最小值是1
[答案]C
4.(辽宁省沈阳二中2008-2009学年上学期高三期中考试,数学,8)定义在[-2,2]上的偶函数 时,
时,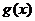 单调递减,若
单调递减,若 则实数m的取值范围是
。
则实数m的取值范围是
。
[解析]本题考查函数的性质,奇偶性,单调性的应用,由题意可知 故
故 解得
解得
[答案]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com