
4.在求轨迹方程问题中易出错的是对轨迹纯粹性及完备性的忽略,因此,在求出轨迹方程以后,应仔细检查有无“不法份子”掺杂其中,将其删除;另一方面,还应注意圾无“漏网之鱼”逍遥法外,将其捉回,即轨迹上点不能含有杂点,也不能少点,也就是曲线上点不多也不少。
[基础闯关]
3.解答曲线的方程问题,首先要明确圆锥曲线的性质,作好对图形变化可能性的总体分析,选好相应的解题策略和拟定好具体的方法,如参数的选取,相关点的变化规律及限制条件等等,注意将动点的几何性质用数学语言表述。
2.要注意一些轨迹问题,都包括一定的隐含条件,也就是曲线上的点的取值范围.
1.求曲线的方程问题是解析几何学的两大基本问题之一,求符合某种条件的动点的轨迹,其实质就是利用题设中几何条件,通过“坐标互化”将其转变为寻求变量间的关系,在求与圆锥曲线有关的轨迹问题时,要特别重视圆锥曲线的定义在求轨迹方程时的作用,只要动点满足已知曲线的定义时,就可以直接得出方程.
3.求曲线方程(或轨迹)常用的方法
(1)直接法:如果动点满足的几何条件本身就是一些几何量的等量关系,或这些几何条件简单明了且易于表达,我们只需把这种关系“翻译”成 的等式就可以得到曲线的方程.由于这种求曲线(轨迹)方程的过程不需要其它步骤,也不需要特殊的技巧,所以称之为直接法;
的等式就可以得到曲线的方程.由于这种求曲线(轨迹)方程的过程不需要其它步骤,也不需要特殊的技巧,所以称之为直接法;
(2)定义法:其动点的轨迹符合某本曲线的定义,则可根据曲线的定义直接求出曲线方程;
(3)几何法:若所求的曲线方程满足某些几何性质(如线段的垂直平分线、角平分线的性质等),则可利用几何法,列出几何式,再代入点的坐标较为方便;
(4)相关点法(代入法):有些问题中,其动点满足的条件不便于用等式列出,但其动点是承受着另一动点(称之为相关点)的运动而运动的.这时我们可以用动点的坐标表示出相关点的坐标,根据相关点所满足的方程即可求得动点的轨迹方程;
(5)参数法:有时动点应满足的几何条件不易得出,也无明显的相关点,但却较易发现(或经过分析可以发现)这个动点的运动常常受到另一个变量(如角度、斜率、比值、截距或时间等)的制约,即动点坐标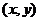 中的
中的 分别随另一变量的变化而变化,我们可称这个变量为参数,建立轨迹的参数方程,这种方法称之为参数法,如需要得出普通方程,只要消去参数即可。在选择参数时,选用的参变量可以具有某种物理或几何性质,如时间、速度、距离、角度、有向线段的数量、直线的斜率,点的横、纵坐标等,也可以没有具体意义,选定参变量还要特别注意它的取值范围对动点坐标取值范围的影响.
分别随另一变量的变化而变化,我们可称这个变量为参数,建立轨迹的参数方程,这种方法称之为参数法,如需要得出普通方程,只要消去参数即可。在选择参数时,选用的参变量可以具有某种物理或几何性质,如时间、速度、距离、角度、有向线段的数量、直线的斜率,点的横、纵坐标等,也可以没有具体意义,选定参变量还要特别注意它的取值范围对动点坐标取值范围的影响.
(6)交轨法:在求动点的轨迹方程时,有时会出现要求两动曲线交点的轨迹问题,这类问题常常通过解方程组得出交点(含参数)的坐标,再消去参考求出所求的曲线方程,该法经常与参数法并用.
(7)整体法:当探求的曲线方程问题较为复杂时,可扩大考察视角,将问题中的条件、结论的各种关系看成是一个整体,从整体出发运用整体思想、注重整体结构的挖掘和分析。
[特别提醒]
2.坐标法与解析研究的对象
(1)坐标法:借助于坐标系,用 表示点,把曲线看成
或轨迹,用曲线上的点的坐标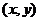 所满足的方程
表示曲线,通过研究方程的性质间接地来研究曲线的性质,这种方法称为坐标法.
所满足的方程
表示曲线,通过研究方程的性质间接地来研究曲线的性质,这种方法称为坐标法.
(2)用坐标法研究几何图形的知识形成的学科叫做 ,解析几何主要研究以下问题:
①根据已知条件,求出曲线的方程;②通过曲线方程,研究曲线的性质.
(3)利用坐标法求曲线方程的步骤:
①建立适当的坐标系,用有序的实数对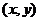 表示曲线上任意一点
表示曲线上任意一点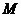 的坐标;
的坐标;
②写出适合条件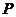 的点
的点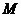 的集合
;
的集合
;
③用坐标表示条件 ,列出方程
,列出方程 ;
;
④化方程 为最简形式;
为最简形式;
⑤说明化简后的方程的解为坐标的点都在 上.
1.曲线的方程与方程的曲线
一般地,在直角坐标系中,如果某曲线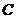 (看作点的集合或适合某种条件的点的轨迹)上的点与一个一元二次方程
(看作点的集合或适合某种条件的点的轨迹)上的点与一个一元二次方程 的实数解建立如下关系:
的实数解建立如下关系:
(1) ;(2) ,那么这个方程就叫做曲线的方程,这条曲线就叫做方程的曲线。另外,平面上所有满足条件的动点的集合,也称为 。
12. (2006年四川卷)已知两定点 ,满足条件
,满足条件 的点
的点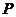 的轨迹是曲线
的轨迹是曲线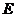 ,直线
,直线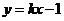 与曲线
与曲线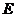 交于
交于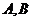 两点,如果
两点,如果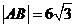 ,且曲线
,且曲线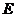 上存在点
上存在点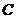 ,使
,使 ,求
,求 的值和
的值和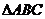 的面积
的面积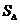 .
.
第五讲 曲线与方程
[知识梳理]
[知识盘点]
11. (2006年福建卷) 已知椭圆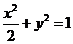 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(I)求过点O、F,并且与椭圆的左准线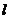 相切的圆的方程;
相切的圆的方程;
(II)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与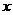 轴交于点G,求点G横坐标的取值范围。
轴交于点G,求点G横坐标的取值范围。
10.在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量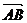 的坐标;
的坐标;
(2)是否存在实数a,使抛物线 上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com