
4.已知两点M(-1,0),N(1,0)且点P使 成公差小于零的等差数列,
成公差小于零的等差数列,
(Ⅰ)点P的轨迹是什么曲线?
(Ⅱ)若点P坐标为 ,
,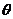 为
为 的夹角,求tanθ。
的夹角,求tanθ。
 例5.如图所示,已知抛物线y2=4px(p>0),O为顶点,A、B为抛物线上的两动点,且满足OA⊥OB,如果OM⊥AB于M点,求点M的轨迹方程.
例5.如图所示,已知抛物线y2=4px(p>0),O为顶点,A、B为抛物线上的两动点,且满足OA⊥OB,如果OM⊥AB于M点,求点M的轨迹方程.
[剖析]点M是OM与AB的交点,点M随着A、B两点的变化而变化,而A、B为抛物线上的动点,点M与A、B的直接关系不明显,因此需引入参数.
[解]解法一:设M(x0,y0),则kOM= ,kAB=-
,kAB=- ,
,
直线AB方程是y=- (x-x0)+y0.由y2=4px可得x=
(x-x0)+y0.由y2=4px可得x= ,将其代入上式,整理,得
,将其代入上式,整理,得
x0y2-(4py0)y-4py02-4px02=0. ①
此方程的两根y1、y2分别是A、B两点的纵坐标,∴A( ,y1)、B(
,y1)、B( ,y2).
,y2).
∵OA⊥OB,∴kOA·kOB=-1.∴ ·
· =-1.∴y1y2=-16p2.
=-1.∴y1y2=-16p2.
根据根与系数的关系,由①可得y1·y2= ,∴
,∴ =16p2.
=16p2.
化简,得x02+y02-4px0=0,即x2+y2-4px=0(除去原点)为所求.
∴点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.
解法二:设A、B两点坐标为A(pt12,2pt1)、B(pt22,2pt2).
∴kOA= ,kOB=
,kOB= ,kAB=
,kAB= .∵OA⊥OB,∴t1·t2=-4.
.∵OA⊥OB,∴t1·t2=-4.
∴AB方程是y-2pt1= (x-pt12), ①
(x-pt12), ①
直线OM的方程是y=- x. ②
x. ②
①×②,得(px)t12+2pyt1-(x2+y2)=0. ③
∴直线AB的方程还可写为y-2pt2= (x-pt22). ④
(x-pt22). ④
由②×④,得(px)t22+(2py)t2-(x2+y2)=0. ⑤
由③⑤可知t1、t2是方程(px)t2+(2py)t2-(x2+y2)=0的两根.
由根与系数的关系可得t1t2= .又t1·t2=-4,
.又t1·t2=-4,
∴x2+y2-4px=0(原点除外)为所求点M的轨迹方程.
故M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.
解法三:设M(x,y),直线AB方程为y=kx+b,由OM⊥AB得k=- .
.
由y2=4px及y=kx+b消去y,得k2x2+x(2kb-4p)+b2=0.
所以x1x2= .消去x,得ky2-4py+4pb=0.所以y1y2=
.消去x,得ky2-4py+4pb=0.所以y1y2= .由OA⊥OB,
.由OA⊥OB,
得y1y2=-x1x2,所以 =-
=- ,b=-4kp.
,b=-4kp.
故y=kx+b=k(x-4p).用k=- 代入,得x2+y2-4px=0(x≠0).
代入,得x2+y2-4px=0(x≠0).
解法四:设点M的坐标为(x,y),直线OA的方程为y=kx,
|
 x.
x.

|
y2=4px,
类似地可得B点的坐标为(4pk2,-4pk),
从而知当k≠±1时,
|

.
直线OM的方程为y=-( -k)x. ②
-k)x. ②
可知M点的坐标同时满足①②,由①及②消去k便得4px=x2+y2,即(x-2p)2+y2=4p2,但x≠0,当k=±1时,容易验证M点的坐标仍适合上述方程.
故点M的轨迹方程为(x-2p)2+y2=4p2(x≠0),
它表示以点(2p,0)为圆心,以2p为半径的圆.
[警示]本题考查了交轨法、参数法求轨迹方程,涉及了类比、分类讨论等数学方法,消参时又用到了整体思想法,对含字母的式子的运算能力有较高的要求,同时还需要注意轨迹的“完备性和纯粹性”.此题是综合考查学生能力的一道好题.
[变式训练]
3. 已知直线l与椭圆 有且仅有一个交点Q,且与x轴、y轴分别交于R、S,求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程.
有且仅有一个交点Q,且与x轴、y轴分别交于R、S,求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程.
 例4.给出定点A(a,0)(a>0)和直线l:x=-1.B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
例4.给出定点A(a,0)(a>0)和直线l:x=-1.B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
[剖析]由直接法得出曲线的方程,再作进一步化简,并判断曲线的形状。
[解]解法一:依题意,记B(-1,b)(b∈R),则直线OA和OB的方程分别为y=0和y=-bx.设点C(x,y),则有0≤x<a,由OC平分∠AOB,知点C到OA、OB距离相等.根据点到直线的距离公式得
|y|= ①
①
依题设,点C在直线AB上,故有:y=- (x-a)
(x-a)
由x-a≠0,得b=- ②
②
将②式代入①式得:y2[1+ ]=[y-
]=[y- ]2.
]2.
整理得:y2[(1-a)x2-2ax+(1+a)y2]=0
若y≠0,则(1-a)x2-2ax+(1+a)y2=0(0<x<a);
若y=0,则b=0,∠AOB=π,点C的坐标为(0,0).满足上式.
综上得点C的轨迹方程为:(1-a)x2-2ax+(1+a)y2=0(0≤x<a).
∵ a≠1,∴ (0≤r<a
(0≤r<a ③
③
由此知,当0<a<1时,方程③表示椭圆弧段;当a>1时,方程③表示双曲线一支的弧段.
解法二:如图,设D是l与x轴的交点,过点C作CE⊥x轴,E是垂足
 (Ⅰ)当|BD|≠0时,设点C(x,y),
(Ⅰ)当|BD|≠0时,设点C(x,y),
则0<x<a,y≠0.
由CE∥BD,得|BD|= (1+a)
(1+a)
∵∠COA=∠COB=∠COD-∠BOD=π-∠COA-∠BOD
∴2∠COA=π-∠BOD
∵tan(2∠COA)= ,tan(π-∠BOD)=-tanBOD,tanCOA=
,tan(π-∠BOD)=-tanBOD,tanCOA= ,tanBOD=
,tanBOD= (1+a)
(1+a)
∴ (1+a)整理得:(1-a)x2-2ax+(1+a)y2=0(0<x<a)
(1+a)整理得:(1-a)x2-2ax+(1+a)y2=0(0<x<a)
(Ⅱ)当|BD|=0时,∠BOA=π,则点C的坐标为(0,0),满足上式
综合(Ⅰ)(Ⅱ),得点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a).
 ∵ a≠1,
∵ a≠1,
∴ (0≤r<a
(0≤r<a (*)
(*)
由此知,当0<a<1时,方程(*)表示椭圆弧段;
当a>1时,方程(*)表示双曲线一支的弧段.
[警示]本题主要考查了曲线与方程,直线和圆锥曲线等基础知识以及求动点轨迹的基本技能和综合运用数学知识解决问题的能力.解法一利用设点法引入参数b,消参数得方程.解法二则利用角之间关系,使用二倍角公式得出等式,化简较简捷,但分析时不容易想.
[变式训练]
2.求过点 所作椭圆
所作椭圆 的弦的中点的轨迹方程.
的弦的中点的轨迹方程.

例3.如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程
[剖析]本题主要考查利用“相关点代入法”求曲线的轨迹方程 利用平面几何的基本知识和两点间的距离公式建立线段AB中点的轨迹方程
利用平面几何的基本知识和两点间的距离公式建立线段AB中点的轨迹方程
[解]设AB的中点为R,坐标为(x,y),则在Rt△ABP中,|AR|=|PR|
又因为R是弦AB的中点,依垂径定理 在Rt△OAR中,|AR|2=|AO|2-|OR|2=36-(x2+y2)
在Rt△OAR中,|AR|2=|AO|2-|OR|2=36-(x2+y2)
又|AR|=|PR|=
所以有(x-4)2+y2=36-(x2+y2),即x2+y2-4x-10=0
因此点R在一个圆上,而当R在此圆上运动时,Q点即在所求的轨迹上运动
设Q(x,y),R(x1,y1),因为R是PQ的中点,所以x1= ,
,
代入方程x2+y2-4x-10=0,得
 -10=0
-10=0
整理得 x2+y2=56,这就是所求的轨迹方程
x2+y2=56,这就是所求的轨迹方程
[警示]对某些较复杂的探求轨迹方程的问题,可先确定一个较易于求得的点的轨迹方程,再以此点作为主动点,所求的轨迹上的点为相关点,求得轨迹方程
[变式训练]
1. 如图所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|= ,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.
例2.如下图,P是抛物线C:y= x2上一点,直线l过点P且与抛物线C交于另一点Q.若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程.
x2上一点,直线l过点P且与抛物线C交于另一点Q.若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程.
|

[解]设P(x1,y1)、Q(x2,y2)、M(x0,y0),依题意知x1≠0,y1>0,y2>0.
由y= x2, ① 得y′=x.
x2, ① 得y′=x.
∴过点P的切线的斜率k切=x1,∴直线l的斜率kl=- =-
=- ,
,
直线l的方程为y- x12=-
x12=- (x-x1) ②
(x-x1) ②
方法一:联立①②消去y,得x2+ x-x12-2=0.∵M为PQ的中点,
x-x12-2=0.∵M为PQ的中点,

|
 =-
=- ,
,
y0= x12-
x12- (x0-x1).
(x0-x1).
消去x1,得y0=x02+ +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+ +1(x≠0).
+1(x≠0).
方法二:由y1= x12,y2=
x12,y2= x22,x0=
x22,x0= ,
,
得y1-y2= x12-
x12- x22=
x22= (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0= =kl=-
=kl=- ,∴x1=-
,∴x1=- .
.
将上式代入②并整理,得y0=x02+ +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+ +1(x≠0).
+1(x≠0).
[警示]本题主要考查了直线、抛物线的基础知识,以及求轨迹方程的常用方法. 与弦的中点有关的问题,可采用“消参法”,即设出弦中点坐标,代入圆锥曲线方程,根据斜率公式,消去参数,得弦中点的轨迹方程;或直接设出弦的两个端的坐标及中点坐标,根据端点坐标适合圆锥曲线方程,联立方程,采用“设点作差”的方法,分析轨迹方程.这种方法相比较而言,“设点作差”(即点差法)的计算过程更为简单,但是一般要知道相交弦的中点坐标时方可采用,有一定的限制性.
[变式训练]
6.高为5 m和3 m的两根旗杆竖在水平地面上,且相距10 m,如果把两旗杆底部的坐标分别确定为A(-5,0)、B(5,0),则地面观测两旗杆顶端仰角相等的点的轨迹方程是_________
[典例精析]
|
 ,tan∠MNP=-2,且△PMN的面积为1,建立适当的坐标系,求以M、N为焦点,且过点P的椭圆的方程.
,tan∠MNP=-2,且△PMN的面积为1,建立适当的坐标系,求以M、N为焦点,且过点P的椭圆的方程.

此应寻找与已知条件和谐统一的未知元,或改造已知条件.
[解]解法一:如上图,过P作PQ⊥MN,垂足为Q,
令|PQ|=m,于是可得|MQ|=|PQ|cot∠PMQ=2m,|QN|=|PQ|cot∠PNQ= m.
m.
|

|MP|= =
= =
= ,|NP|=
,|NP|= =
= =
= .
.
以MN的中点为原点,MN所在直线为x轴建立直角坐标系,设椭圆方程为 +
+ =1(a>b>0).则2a=|MP|+|NP|=
=1(a>b>0).则2a=|MP|+|NP|= ,2c=|MN|=
,2c=|MN|= ,故所求椭圆方程为
,故所求椭圆方程为 +
+ =1.
=1.
解法二:设M(-c,0)、N(c,0),P(x,y),y>0,

 =
= ,
,
|
 =2,
=2,
y·c=1,
解之,得x= ,y=
,y= ,c=
,c= .
.
设椭圆方程为b2x2+a2y2=a2b2,则
 b2·(
b2·( )2+a2(
)2+a2( )2=a2b2,
)2=a2b2,
a2-b2= ,
,
解之,得a2= ,b2=3.故所求椭圆方程为
,b2=3.故所求椭圆方程为 +
+ =1.
=1.
[警示]解法一选择了与a较接近的未知元|PM|、|PN|,但需改造已知条件,以便利用正弦定理和面积公式;解法二以条件为主,选择了与条件联系最直接的未知元x、y、c.本题解法较多,但最能体现方程思想方法的、学生易于理解和接受的是这两种解法.
[变式训练]:
5.△ABC中,A为动点,B、C为定点,B(- ,0),C(
,0),C( ,0),且满足条件sinC-sinB=
,0),且满足条件sinC-sinB= sinA,则动点A的轨迹方程为_________
sinA,则动点A的轨迹方程为_________
4.若 ,则
,则 的焦点
的焦点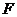 的轨迹方程是( )
的轨迹方程是( )
A. B.
B. C.
C. D.
D.
3.在同一坐标系中,方程a2x2+b2y2=1与ax+by2=0(a>b>0)的曲线大致是( )

2.x= 表示的曲线是( )
表示的曲线是( )
A.双曲线 B.椭圆
C.双曲线的一部分 D.椭圆的一部分
1.已知椭圆的焦点是F1、F2,P是椭圆上的一个动点.如果延长F1P到Q,使得|PQ|=|PF2|,那么动点Q的轨迹是( )
A.圆 B.椭圆
C.双曲线的一支 D.抛物线
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com