
(17)(本小题满分10分)(注意:在试题卷上作答无效)
设等差数列{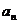 }的前
}的前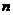 项和为
项和为 ,公比是正数的等比数列{
,公比是正数的等比数列{ }的前
}的前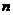 项和为
项和为 ,
,
已知 的通项公式.
的通项公式.
(18)(本小题满分12分)(注意:在试用题卷上作答无效)
在 中,内角A、b、c的对边长分别为a、b、c.已知
中,内角A、b、c的对边长分别为a、b、c.已知 ,且
,且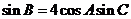 ,求b.
,求b.
(19)(本小题满分12分)(注决:在试题卷上作答无效)
如图,四棱锥 中,底面
中,底面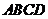 为矩形,
为矩形,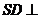 底面
底面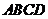 ,
,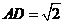 ,
,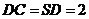 ,点
,点 在侧棱
在侧棱 上,
上, 。
。
 证明:
证明: 是侧棱
是侧棱 的中点;
的中点;
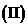 求二面角
求二面角 的大小。
的大小。

(20)(本小题满分12分)(注意:在试题卷上作答无效)
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(Ⅰ)求再赛2局结束这次比赛的概率;
(Ⅱ)求甲获得这次比赛胜利的概率。
(21)(本小题满分12分)(注意:在试题卷上作答无效)
已知函数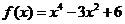 .
.
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)设点P在曲线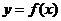 上,若该曲线在点P处的切线
上,若该曲线在点P处的切线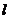 通过坐标原点,求
通过坐标原点,求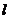 的方程
的方程
(22)(本小题满分12分)(注意:在试题卷上作答无效)
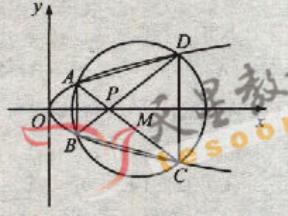
如图,已知抛物线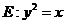
 与圆
与圆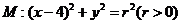 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。
(Ⅰ)求r的取值范围
(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
本资料由《七彩教育网》 提供!
(注意:在试题卷上作答无效)
(13)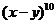 的展开式中,
的展开式中, 的系数与
的系数与 的系数之和等于_____________.
的系数之和等于_____________.
(14)设等差数列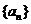 的前
的前 项和为
项和为 。若
。若 ,则
,则 _______________.
_______________.
(15)已知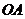 为球
为球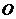 的半径,过
的半径,过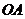 的中点
的中点 且垂直于
且垂直于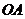 的平面截球面得到圆
的平面截球面得到圆 ,若圆
,若圆 的面积为
的面积为 ,则球
,则球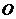 的表面积等于__________________.
的表面积等于__________________.
(16)若直线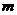 被两平行线
被两平行线 所截得的线段的长为
所截得的线段的长为 ,则
,则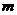 的倾斜角可以是
的倾斜角可以是
① ②
② ③
③ ④
④ ⑤
⑤
其中正确答案的序号是 .(写出所有正确答案的序号)
3.本卷共10小题,共90分.
(1)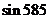 的值为
的值为
(A) 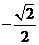 (B)
(B) (C)
(C) (D)
(D) 
(2)设集合A={4,5,6,7,9},B={3,4,7,8,9},全集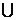 =A
=A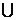 B,则集合[u (A
B,则集合[u (A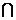 B)中的元素共有
B)中的元素共有
(A) 3个 (B) 4个 (C)5个 (D)6个
(3)不等式 的解集为
的解集为
(A)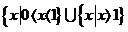 (B)
(B)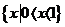
(C)  (D)
(D)
(4)已知tan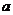 =4,cot
=4,cot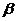 =
= ,则tan(a+
,则tan(a+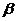 )=
)=
(A) (B)
(B) (C)
(C)  (D)
(D) 
(5)设双曲线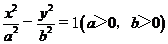 的渐近线与抛物线
的渐近线与抛物线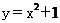 相切,则该双曲线的离心率等于
相切,则该双曲线的离心率等于
(A) (B)2 (C)
(B)2 (C) (D)
(D)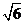
(6)已知函数 的反函数为
的反函数为 ,则
,则
(A)0 (B)1 (C)2 (D)4
(7)甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学,若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有
(A)150种 (B)180种 (C)300种 (D)345种
(8)设非零向量 满足
满足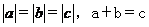 ,则
,则
(A)150°B)120° (C)60° (D)30°
(9)已知三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的射影为
上的射影为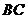 的中点,则异面直线
的中点,则异面直线 与
与 所成的角的余弦值为
所成的角的余弦值为
(A)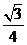 (B)
(B)  (C)
(C) 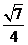 (D)
(D)

(10) 如果函数 的图像关于点
的图像关于点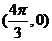 中心对称,那么
中心对称,那么 的最小值为
的最小值为
(A)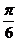 (B)
(B)  (C)
(C)  (D)
(D)

(11)已知二面角 为600 ,动点P、Q分别在面
为600 ,动点P、Q分别在面 内,P到
内,P到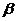 的距离为
的距离为 ,Q到
,Q到 的距离为
的距离为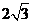 ,则P、Q两点之间距离的最小值为
,则P、Q两点之间距离的最小值为
(12)已知椭圆 的右焦点为F,右准线
的右焦点为F,右准线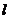 ,点
,点 ,线段AF交C于点B。若
,线段AF交C于点B。若
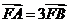 ,则
,则 =
=
(A) 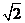 (B) 2 (C)
(B) 2 (C)  (D) 3
(D) 3
2009年普通高等学校招生全国统一考试
文科数学(必修 选修Ⅰ)
选修Ⅰ)
第Ⅱ卷
2.第Ⅱ卷共7页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.
22.已知函数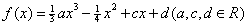 满足
满足 且
且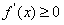 在R上恒成立.
在R上恒成立.
求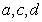 的值.
的值.
是否存在实数m,使函数 在区间
在区间 上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
附加题:(30分)
已知函数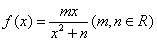 在x=1处取得极值2.
在x=1处取得极值2.
(1) 求f(x)的解析式;
(2) 设A是曲线y=f(x)上除原点O外的任意一点,过OA的中点且垂直于x轴的直线交曲线于点B。试问:是否存在这样的点A,使得曲线在点B处的切线与OA平行?若存在,求出点A的坐标;若不存在,说明理由。
(3) 设函数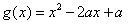 。若对于任意的
。若对于任意的 ,总存在
,总存在 ,使得
,使得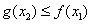 ,求实数a的取值范围。
,求实数a的取值范围。
21.设函数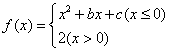 ,其中
,其中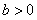 ,
, .当且仅当
.当且仅当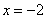 时,函数
时,函数 取得最小值
取得最小值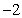
(Ⅰ)求函数 的表达式;
的表达式;
(Ⅱ)若方程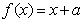
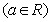 至少有两个不相同的实数根,求
至少有两个不相同的实数根,求 取值的集合.
取值的集合.
20. 已知某企业原有员工2000人,每人每年可为企业创利润3.5万元.为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗,为维护生产稳定,该企业决定待岗人数不超过原有员工的5%,并且每年给每位待岗员工发放生活补贴0.5万元.据评估,当待岗员工人数x为x人,留岗员工每人每年可为企业多创利润 万元;为使企业年利润最大,应安排多少员工待岗?
万元;为使企业年利润最大,应安排多少员工待岗?
19.一个盒中放有除颜色不同外,其余完全相同的黑球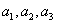 和白球
和白球 。
。
(1)从盒中同时摸出两个球,求两个球颜色恰好相同的概率;
(2) 从盒中摸出一个球,放回后再摸出一个球,求两个球颜色恰好不同的概率.
18.已知条件 和条件
和条件 ,请选取适当的实数
,请选取适当的实数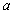 的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com