
6.(2007·江苏,10)在平面直角坐标系xOy中,已知平面区域A={(x,y)|x+y≤1,且x≥0,y≥0},则平面区域B={(x+y,x-y)|(x,y)∈A}的面积为 ( )
?A.2 B.1 C.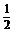 D.
D.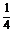
答案?B?
5.(2009·武汉模拟)如果实数x,y满足 目标函数z=kx+y的最大值为12,最小值为3,那么实数k的值为 ( )
目标函数z=kx+y的最大值为12,最小值为3,那么实数k的值为 ( )
?A.2? B.-2? C.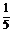 ? D.不存在
? D.不存在
答案?A?
4.(2008·山东理,12)设二元一次不等式组 所表示的平面区域为M,使函数y=ax(a>0,a≠1)的图象过区域M的a的取值范围是 ( )
所表示的平面区域为M,使函数y=ax(a>0,a≠1)的图象过区域M的a的取值范围是 ( )
?A.[1,3]? B.[2,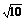 ] C.[2,9]? D.[
] C.[2,9]? D.[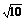 ,9]
,9]
答案?C?
3.已知平面区域D由以A(1,3)、B(5,2)、C(3,1)为顶点的三角形内部和边界组成.若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,则m等于 ( )
?A.-2? B.-1? C.1 D.4
答案?C?
2.若不等式组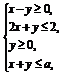 表示的平面区域是一个三角形,则a的取值范围是 ( )
表示的平面区域是一个三角形,则a的取值范围是 ( )
?A.a≥ B.0<a≤1
B.0<a≤1
?C.1≤a≤ ?
D.0<a≤1或a≥
?
D.0<a≤1或a≥
答案?D?
1.(2008·全国Ⅱ理,5)设变量x,y满足约束条件: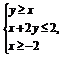 则z=x-3y的最小值为 ( )
则z=x-3y的最小值为 ( )
?A.-2 ?B.-4? C.-6 ?D.-8
答案?D
3.某家具公司制作木质的书桌和椅子两种家具,需要木工和漆工两道工序,已知木工平均四个小时做一把椅子,八个小时做一张书桌,该公司每星期木工最多有8 000个工作时;漆工平均两小时漆一把椅子,一个小时漆一张书桌,该公司每星期漆工最多有1 300个工作时.又已知制作一把椅子和一张书桌的利润分别是15元和20元,根据以上条件,怎样安排生产能获得最大利润?
解 依题意设每星期生产x把椅子,y张书桌,
那么利润p=15x+20y.
其中x,y满足限制条件 .
.
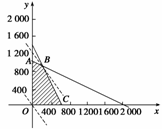
即点(x,y)的允许区域为图中阴影部分,它们的边界分别为4x+8y=8 000 (即AB),2x+y=1 300(即BC),x=0(即OA)和y=0(即OC).
对于某一个确定的 =
= 满足
满足 =15x+20y,且点(x,y)属于
=15x+20y,且点(x,y)属于
解x,y就是一个能获得 元利润的生产方案.
元利润的生产方案.
对于不同的p,p=15x+20y表示一组斜率为- 的平行线,且p越大,相应的直线位置越高;p越小,相应的直线位置越低.按题意,要求p的最大值,需把直线p=15x+20y尽量地往上平移,又考虑到x,y的允许范围,
的平行线,且p越大,相应的直线位置越高;p越小,相应的直线位置越低.按题意,要求p的最大值,需把直线p=15x+20y尽量地往上平移,又考虑到x,y的允许范围,
当直线通过B点时,处在这组平行线的最高位置,此时p取最大值.
由 ,得B(200,900),
,得B(200,900),
当x=200,y=900时,p取最大值,
即pmax=15×200+20×900=21 000,
即生产200把椅子、900张书桌可获得最大利润21 000元.

2.(2008·全国Ⅰ理,13)若x,y满足约束条件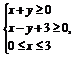 则z=2x-y的最大值为 .
则z=2x-y的最大值为 .
答案 9
1.(2008·浙江理,17)若a≥0,b≥0,且当 时,恒有ax+by≤1,则以a,b为坐标的点P(a,b)所形成的平面区域的面积等于 .
时,恒有ax+by≤1,则以a,b为坐标的点P(a,b)所形成的平面区域的面积等于 .
答案 1
5.(2008·福建理,8)若实数x、y满足 则
则 的取值范围是 ( )
的取值范围是 ( )
?A.(0,1) B.(0,1] C.(1,+∞) D.[1,+∞)
答案?C?

例1 画出不等式组 表示的平面区域,并回答下列问题:
表示的平面区域,并回答下列问题:
(1)指出x,y的取值范围;
(2)平面区域内有多少个整点?
解 (1)不等式x-y+5≥0表示直线x-y+5=0上及右下方的点的集合.x+y≥0表示直线x+y=0上及右上方的点的集合, x≤3表示直线x=3上及左方的点的集合.

则U. 所以,不等式组 .
.
表示的平面区域如图所示.
结合图中可行域得
x ,y
,y [-3,8].
[-3,8].
(2)由图形及不等式组知

当x=3时,-3≤y≤8,有12个整点;
当x=2时,-2≤y≤7,有10个整点;
当x=1时,-1≤y≤6,有8个整点;
当x=0时,0≤y≤5,有6个整点;
当x=-1时,1≤y≤4,有4个整点;
当x=-2时,2≤y≤3,有2个整点;
∴平面区域内的整点共有
2+4+6+8+10+12=42(个).
例2 (2008·湖南理,3)已知变量x、y满足条件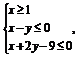 则x+y的最大值是 ( )
则x+y的最大值是 ( )
?A.2? B.5 ?C.6 ?D.8
答案?C?
例3 (12分)某工厂生产甲、乙两种产品,计划每天每种产品的生产量不少于15吨,已知生产甲产品
1吨,需煤9吨,电力4千瓦时,劳力3个;生产乙产品1吨,需煤4吨,电力5千瓦时,劳力10个;甲产品每吨的利润为7万元,乙产品每吨的利润为12万元;但每天用煤不超过300吨,电力不超过200千瓦时,劳力只有300个.问每天生产甲、乙两种产品各多少吨,才能使利润总额达到最大?
解 设每天生产甲、乙两种产品分别为x吨、y吨,利润总额为z万元, 1分
则线性约束条件为 4分
4分
目标函数为z=7x+12y, 6分
作出可行域如图, 8分
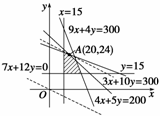
作出一组平行直线7x+12y=t,当直线经过直线4x+5y=200和直线3x+10y=300的交点A(20,24)时,利润最大. 10分
即生产甲、乙两种产品分别为20吨、24吨时,利润总额最大,zmax=7×20+12×24=428(万元).
答 每天生产甲产品20吨、乙产品24吨,才能使利润总额达到最大. 12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com