4.(2008·北京理，4)若点P到直线x=-1的距离比它到点(2，0)的距离小1，则点P的轨迹为(　　 )　A.圆　　　　　　　　　　 　　　　　　　　　　　 ?B.椭圆

?C.双曲线　　　　　　　　　　　　　　　　　　　　 ?D.抛物线　

答案?D?　

3.动点P到两坐标轴的距离之和等于2，则点P的轨迹所围成的图形面积是　　　　　　　 (　　 )　

?A.2　　　　　　　　　 　　 B.4 　　　　　　　　　 C.8　　　　　　　　　　 ?D.不存在　

答案?C?　

2.到两定点A(0，0)，B(3，4)距离之和为5的点的轨迹是　 　　　　　　　　　　　 (　　 )　

?A.椭圆　　　　　　　　　　　　　　　　 ?　 　　　 B.AB所在的直线　

?C.线段AB?　　　　　　　　　　　　　　　　 　　　 D.无轨迹　

答案?C?　

1.已知坐标满足方程F(x，y)=0的点都在曲线C上，那么　　　　　　　　　　　　　　 (　　 )　

?A.曲线C上的点的坐标都适合方程F(x，y)=0　

?B.凡坐标不适合F(x，y)=0的点都不在C上　

?C.不在C上的点的坐标有些适合F(x，y)=0，有些不适合F(x，y)=0　

?D.不在C上的点的坐标必不适合F(x，y)=0　

答案?D?　

12.在R上可导的函数f(x)=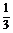x³+ax²+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时取得极小值,求点(a,b)对应的区域的面积以及的取值范围.

解 函数f(x)的导数为f′(x)=x²+ax+2b,当x∈(0,1)时,f(x)取得极大值,当x∈(1,2)时,f(x)取得极小值,则方程x²+ax+2b=0有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内,由二次函数f′(x)=x²+ax+2b的图象与方程x²+ax+2b=0根的分布之间的关系可以得到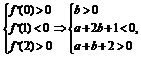

在aOb平面内作出满足约束条件的点(a,b)对应的区域为△ABD(不包括边界),

如图阴影部分,其中点A(-3,1),B(-1,0),D(-2,0),　

△ABD的面积为　

S_△ABD=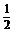|BD|×h=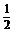(h为点A到a轴的距离).　

点C(1,2)与点(a,b)连线的斜率为,　

显然(k_CA,k_CB),　

即

§7.4 曲线与方程

基础自测

11.两种大小不同的钢板可按下表截成A,B,C三种规格成品:　

	A规格	B规格	C规格
第一种钢板	2	1	1
第二种钢板	1	2	3

某建筑工地需A，B，C三种规格的成品分别为15，18，27块，问怎样截这两种钢板，可得所需三种规格成品，且所用钢板张数最小.　

解 设需要第一种钢板x张，第二种钢板y张，钢板总数为z张，z=x+y,　

约束条件为：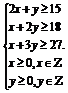

作出可行域如图所示：　

令z=0，作出基准直线l:y=-x,平行移动直线l发现在可行域内，经过直线x+3y=27和直线2x+y=15的交点A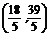可使z取最小，由于都不是整数，而最优解(x,y)中，x,y必须都是整数，可行域内点A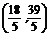不是最优解；　

通过在可行域内画网格发现，经过可行域内的整点且与A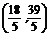点距离最近的直线是x+y=12,经过的整点是B(3,9)和C(4，8)，它们都是最优解.　

答 要截得所需三种规格的钢板，且使所截两种钢板的张数最少的方法有两种：　

第一种截法是截第一种钢板3张，第二种钢板9张；　

第二种截法是截第一种钢板4张，第二种钢板8张；　

两种方法都最少要截两种钢板共12张.

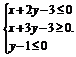10.已知变量x,y满足的约束条件为若目标函数z=ax+y(其中a＞0)仅在点(3，0)处取得最大值，求a的取值范围.　

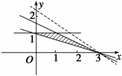
解 依据约束条件，画出可行域.　

∵直线x+2y-3=0的斜率k₁=-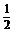,目标函数z=ax+y (a＞0)对应直线的斜率k₂=-a,若符合题意，则须k₁＞k₂,即-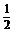＞-a,得a＞.

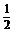9.已知实数x、y满足，试求z=的最大值和最小值.　

解　 由于z==，　

所以z的几何意义是点(x,y)与点M(-1，-1)连线的斜率，因此的最值就是点(x，y)与点

M(-1，-1)连线的斜率的最值，　

结合图可知：直线MB的斜率最大，直线MC的斜率最小，即z_max=k_MB=3，此时x=0，y=2；　

z_min=k_MC=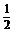，此时x=1，y=0.

8.设集合A={(x,y)|y≥|x-2|,x≥0},B={(x,y)|y≤-x+b},A∩B≠.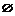　

(1)b的取值范围是　　　 ；　

(2)若(x,y)∈A∩B,且x+2y的最大值为9,则b的值是　　　　 .　

答案 (1)［2,+∞) (2)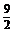　

7.(2008·安徽理，15)若A为不等式组，表示的平面区域，则当a从-2连续变化到1时，动直线x+y=a扫过A中的那部分区域的面积为　　　　　 .　

答案