
5.能够使得圆x2+y2-2x+4y+1=0上恰有两个点到直线2x+y+c=0距离等于1的c的一个值为 ( )
?A.2 ? B.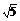 ? C.3? D.3
? C.3? D.3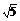
答案?C?
4.(2008·全国Ⅰ文,10)若直线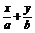 =1与圆x2+y2=1有公共点,则 ( ) A.a2+b2≤1 B.a2+b2≥1?
C.
=1与圆x2+y2=1有公共点,则 ( ) A.a2+b2≤1 B.a2+b2≥1?
C. ≤1 ?D.
≤1 ?D. ≥1
≥1
答案?D?
3.已知圆C:(x-a)2+(y-2)2=4 (a>0)及直线l:x-y+3=0,当直线l被圆C截得的弦长为2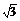 时,则a
时,则a
等于 ( ) A.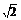 ? B.2-
? B.2-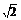 ? C.
? C.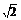 -1 ?D.
-1 ?D.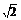 +1
+1
答案?C?
2.(2008·重庆理,3)圆O1:x2+y2-2x=0和圆O2:x2+y2-4y=0的位置关系是 ( )
?A.相离 ?B.相交 ?C.外切 ?D.内切
答案?B?
1.(2008·辽宁理,3)圆x2+y2=1与直线y=kx+2没有公共点的充要条件是 ( )
?A. ? B.
? B.
?C.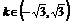 ? D.
? D. 
答案?C?
4.圆x2+y2=8内一点P(-1,2),过点P的直线l的倾斜角为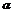 ,直线l交圆于A、B两点.
,直线l交圆于A、B两点.
(1)当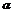 =
=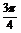 时,求AB的长;
时,求AB的长;
(2)当弦AB被点P平分时,求直线l的方程.
解 (1)当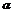 =
=
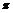 时,kAB=-1,
时,kAB=-1,
直线AB的方程为y-2=-(x+1),
即x+y-1=0.
故圆心(0,0)到AB的距离
d= ,
,
从而弦长|AB|=2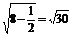 .
.
(2)设A(x1,y1),B(x2,y2),
则x1+x2=-2,y1+y2=4.
由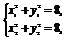
两式相减得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,
即-2(x1-x2)+4(y1-y2)=0,
∴kAB=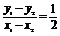 .
.
∴直线l的方程为y-2=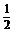 (x+1),
(x+1),
即x-2y+5=0.

3.求过点P(4,-1)且与圆C:x2+y2+2x-6y+5=0切于点M(1,2)的圆的方程.
解 方法一 设所求圆的圆心为A(m,n),半径为r,
则A,M,C三点共线,且有|MA|=|AP|=r,
因为圆C:x2+y2+2x-6y+5=0的圆心为C(-1,3),
则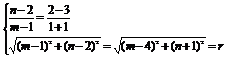 ,
,
解得m=3,n=1,r=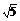 ,
,
所以所求圆的方程为(x-3)2+(y-1)2=5.
方法二 因为圆C:x2+y2+2x-6y+5=0过点M(1,2)的切线方程为2x-y=0,
所以设所求圆A的方程为
x2+y2+2x-6y+5+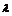 (2x-y)=0,
(2x-y)=0,
因为点P(4,-1)在圆上,所以代入圆A的方程,
解得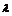 =-4,
=-4,
所以所求圆的方程为x2+y2-6x-2y+5=0.
2.从圆C:x2+y2-4x-6y+12=0外一点P(a,b)向圆引切线PT,T为切点,且|PT|=|PO| (O为原点).
求|PT|的最小值及此时P的坐标.
解 已知圆C的方程为
(x-2)2+(y-3)2=1,
∴圆心C的坐标为(2,3),
半径r=1.
如图所示,连结PC,CT,
由平面几何知,
PT2=PC2-CT2
=(a-2)2+(b-3)2-1.
由已知,PT=PO,∴PT2=PO2,
即(a-2)2+(b-3)2-1=a2+b2.
化简得2a+3b-6=0.
得PT2=a2+b2= (13a2-24a+36).
(13a2-24a+36).
当a= 时,
时,
PTmin=
|PT|的最小值为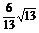 ,
,
此时点P的坐标是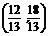 .
.
1.m为何值时,直线2x-y+m=0与圆x2+y2=5.
(1)无公共点;
(2)截得的弦长为2;
(3)交点处两条半径互相垂直.
解 (1)由已知,圆心为O(0,0),半径r=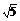 ,
,
圆心到直线2x-y+m=0的距离
d=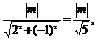
∵直线与圆无公共点,∴d>r,即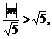 ,
,
∴m>5或m<-5.
故当m>5或m<-5时,直线与圆无公共点.
 (2)如图所示,由平面几何垂径定理知
(2)如图所示,由平面几何垂径定理知
r2-d2=12,即5-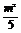 =1.
=1.
得m=±2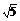 ,
,
∴当m=±2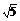 时,直线被圆截得的弦长为2.
时,直线被圆截得的弦长为2.
 (3)如图所示,由于交点处两条半径互相垂直,
(3)如图所示,由于交点处两条半径互相垂直,
∴弦与过弦两端的半径组成等腰直角三角形,
∴d=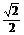 r,即
r,即 =
=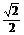 ·
·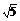 ,
,
解得m=± .
.
故当m=± 时,直线与圆在两交点处的两条半径互相垂直.
时,直线与圆在两交点处的两条半径互相垂直.
5.(2008·重庆理,15)直线l与圆x2+y2+2x-4y+a=0 (a<3)相交于两点A,B,弦AB的中点为(0,1),则直线l的方程为 .
答案 x-y+1=0

例1 已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0(m∈R).
(1)求证:不论m为何值,圆心在同一直线l上;
(2)与l平行的直线中,哪些与圆相交、相切、相离;
(3)求证:任何一条平行于l且与圆相交的直线被各圆截得的弦长相等.
(1)证明 配方得:(x-3m)2+[y-(m-1)]2=25,
设圆心为(x,y),则 消去m得
消去m得
l:x-3y-3=0,则圆心恒在直线l:x-3y-3=0上.
(2)解 设与l平行的直线是l1:x-3y+b=0,
则圆心到直线l1的距离为
d=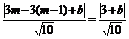 .
.
∵圆的半径为r=5,
∴当d<r,即-5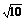 -3<b<5
-3<b<5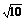 -3时,直线与圆相交;
-3时,直线与圆相交;
当d=r,即b=±5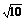 -3时,直线与圆相切;
-3时,直线与圆相切;
当d>r,即b<-5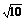 -3或b>5
-3或b>5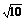 -3时,直线与圆相离.
-3时,直线与圆相离.
(3)证明 对于任一条平行于l且与圆相交的直线l1:x-3y+b=0,由于圆心到直线l1的距离d= ,
,
弦长=2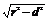 且r和d均为常量.
且r和d均为常量.
∴任何一条平行于l且与圆相交的直线被各圆截得的弦长相等.
 例2 从点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程.
例2 从点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程.
解 方法一 如图所示,设l与x轴交于点B(b,0),则kAB=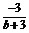 ,根据光的反射定律,
,根据光的反射定律,
反射光线的斜率k反=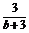 .
.
∴反射光线所在直线的方程为
y=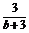 (x-b),
(x-b),
即3x-(b+3)y-3b=0.
∵已知圆x2+y2-4x-4y+7=0的圆心为C(2,2),
半径为1,
∴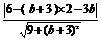 =1,解得b1=-
=1,解得b1=- ,b2=1.
,b2=1.
∴kAB=- 或kAB=-
或kAB=- .
.
∴l的方程为4x+3y+3=0或3x+4y-3=0.
方法二 已知圆C:x2+y2-4x-4y+7=0关于x轴对称的圆为C1:(x-2)2+(y+2)2=1,其圆心C1的坐标为(2,-2),半径为1,由光的反射定律知,入射光线所在直线方程与圆C1相切.
设l的方程为y-3=k(x+3),则 =1,
=1,
即12k2+25k+12=0.
∴k1=- ,k2=-
,k2=- .
.
则l的方程为4x+3y+3=0或3x+4y-3=0.
方法三 设入射光线方程为y-3=k(x+3),反射光线所在的直线方程为y=-kx+b,由于二者横截距相等,且后者与已知圆相切.
∴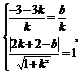 消去b得
消去b得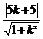 =1.
=1.
即12k2+25k+12=0,∴k1=- ,k2=-
,k2=- .
.
则l的方程为4x+3y+3=0或3x+4y-3=0.
例3 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,m为何值时,(1)圆C1与圆C2相外切;(2)圆C1与圆C2内含?
解 对于圆C1与圆C2的方程,经配方后
C1:(x-m)2+(y+2)2=9; C2:(x+1)2+(y-m)2=4.
(1)如果C1与C2外切,则有 =3+2.
=3+2.
(m+1)2+(m+2)2=25.
m2+3m-10=0,解得m=-5或m=2.
(2)如果C1与C2内含,则有 <3-2.
<3-2.
(m+1)2+(m+2)2<1,m2+3m+2<0,
得-2<m<-1,
∴当m=-5或m=2时,圆C1与圆C2外切;
当-2<m<-1时,圆C1与圆C2内含.
例4(12分)已知点P(0,5)及圆C:x2+y2+4x-12y+24=0.
(1)若直线l过P且被圆C截得的线段长为4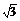 ,求l的方程;
,求l的方程;
(2)求过P点的圆C的弦的中点的轨迹方程.
解 (1)方法一 如图所示,AB=4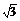 ,D是AB的中点,CD⊥AB,AD=2
,D是AB的中点,CD⊥AB,AD=2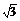 ,圆x2+y2+4x-12y+24=0可化为(x+2)2+(y-6)2=16,圆心C(-2,6),半径r=4,故AC=4,
,圆x2+y2+4x-12y+24=0可化为(x+2)2+(y-6)2=16,圆心C(-2,6),半径r=4,故AC=4,
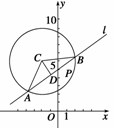 在Rt△ACD中,可得CD=2.
2分
在Rt△ACD中,可得CD=2.
2分
设所求直线的斜率为k,则直线的方程为y-5=kx,
即kx-y+5=0.
由点C到直线AB的距离公式: =2,得k=
=2,得k= .
.
此时直线l的方程为3x-4y+20=0. 4分
又直线l的斜率不存在时,此时方程为x=0. 6分
则y2-12y+24=0,∴y1=6+2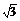 ,y2=6-2
,y2=6-2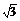 ,
,
∴y2-y1=4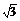 ,故x=0满足题意.
,故x=0满足题意.
∴所求直线的方程为3x-4y+20=0或x=0. 8分
方法二 设所求直线的斜率为k,则直线的方程为
y-5=kx,即y=kx+5,
联立直线与圆的方程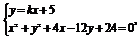
消去y得(1+k2)x2+(4-2k)x-11=0 ① 2分
设方程①的两根为x1,x2,
由根与系数的关系得 ② 4分
② 4分
由弦长公式得 |x1-x2|=
|x1-x2|=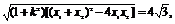
将②式代入,解得k= ,
,
此时直线的方程为3x-4y+20=0. 6分
又k不存在时也满足题意,此时直线方程为x=0.
∴所求直线的方程为x=0或3x-4y+20=0. 8分
(2)设过P点的圆C的弦的中点为D(x,y),
则CD⊥PD,即 ·
· =0, 10分
=0, 10分
(x+2,y-6)·(x,y-5)=0,化简得所求轨迹方程为
x2+y2+2x-11y+30=0. 12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com