
2.(2009重庆卷文)已知 ,则
,则 的最小值是( )
的最小值是( )
A.2 B.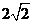 C.4 D.5
C.4 D.5
答案 C
解析 因为 当且仅当
当且仅当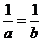 ,且 ,即
,且 ,即 时,取“=”号。
时,取“=”号。
1.(2009天津卷理)设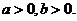 若
若 的最小值为
的最小值为
A . 8 B . 4 C.
1 D. 
考点定位 本小题考查指数式和对数式的互化,以及均值不等式求最值的运用,考查了变通能力。
答案 C
解析 因为 ,所以
,所以 ,
,
 ,当且仅当
,当且仅当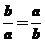 即
即 时“=”成立,故选择C
时“=”成立,故选择C
2009年高考题
10.选木箱、人和小车组成的系统为研究对象,取向右为正方向.设第n次推出木箱后人与小车的速度为vn,第n次接住后速度为vn′,则由动量守恒定律可知:
第一次推出后有:0=Mv1-mv,则v1=mv/M
第一次接住后有:Mv1+mv=(M+m)v1′
第二次推出后有:(M+m)v1′=Mv2-mv,则v2=3mv/M
第二次接住后有:Mv2+mv=(M+m)v2′……
第n-1次接住:Mvn-1+mv=(M+m)vn-1
第n次推出:(M+m)vn-1′=Mvn-mv 即vn=(2n-1)mv/M
设最多能推N次,推出后有vn≥v vn-1≤v 即 ≥v,且
≥v,且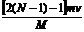 <v
<v
所以 ≤ N <
≤ N <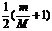 + 1 将M/m=4代入,可得: 2.5≤N<3.5
+ 1 将M/m=4代入,可得: 2.5≤N<3.5
因N取整数,故N=3
9.(1)射出第一颗子弹时,设船的速度为V1,由动量守恒定律得 ,
,
(2)每射出一颗子弹的过程,系统的动量均守恒,而每一颗子弹进入靶中后,船的速度将为零,故每一颗子弹射出时,船后退的速度是相同的,
即
(3)每发射一颗子弹的过程实际上经历了三个阶段:第一阶段是击发到子弹射出枪瞠为止;第二个阶段是子弹在空中飞行的阶段;第三个阶段是子弹从击中靶子到静止为止.三个阶段都遵从动量守恒定律,第一、第三阶段历时很短,故这两个阶段船的移动可忽略.因此每发射一颗子弹的过程,只在第二阶段船向后移动.每发射完一颗子弹后船向移动的距离
8. (1)由动量守恒得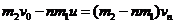 小车开始反向
小车开始反向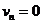 得
得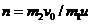
(2)发射相邻两 枚弹丸的时间间隔就是发射第K(K〈1〉颗弹丸后小车的周期,即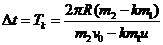 且
且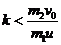
6. 7.
7. 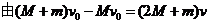
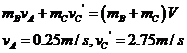
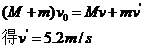
1.A、 2.B、 3.CD 4.BC 5. 
10.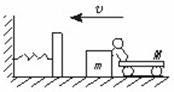 如图所示,光滑水平面上停放一个木箱和小车,木箱的质量为m,小车和人总的质量为M,M∶m=4∶1, 人以速率v沿水平方向将木箱推出,木箱被挡板以原速反弹回来以后,人接住木箱再以同样大小的速度v第二次推出木箱,木箱又被原速反弹……,问人最多能推几次木箱?
如图所示,光滑水平面上停放一个木箱和小车,木箱的质量为m,小车和人总的质量为M,M∶m=4∶1, 人以速率v沿水平方向将木箱推出,木箱被挡板以原速反弹回来以后,人接住木箱再以同样大小的速度v第二次推出木箱,木箱又被原速反弹……,问人最多能推几次木箱?
动量守恒定律适应练习答案
9.某人在一只静止的小船上练习射击.已知船、人连同枪(不包括子弹)及靶的总质量为M,枪内装有n颗子弹,每颗子弹的质量为m,枪口到靶的距离为L,子弹飞出枪口时相对于地面的速度为v.若在发射后一颗子弹时,前一颗子弹已陷入固定在船上的靶中,不计水对船的阻力.问
(1)射出第一颗子弹时,船的速度多大,
(2)发射第n颗子弹时,船的速度多大?
(3)发射完颗n子弹后,船一共能向后移动多少距离?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com