
5.定义区间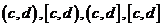 的长度均为
的长度均为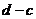 ,其中
,其中 。已知实数
。已知实数 ,则满足
,则满足 的
的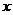 构成的区间的长度之和为(
)。
构成的区间的长度之和为(
)。
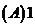



答 选 。
。
原不等式等价于 。
。
当 或
或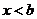 时,原不等式等价于
时,原不等式等价于 。设
。设 ,则
,则 。设
。设 的两个根分别为
的两个根分别为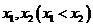 ,则满足
,则满足 的
的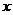 构成的区间为
构成的区间为 ,区间的长度为
,区间的长度为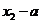 。
。
当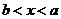 时,同理可得满足
时,同理可得满足 的
的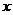 构成的区间为
构成的区间为 ,区间的长度为
,区间的长度为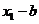 。
。
由韦达定理, ,所以满足条件的
,所以满足条件的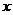 构成的区间的长度之和为
构成的区间的长度之和为 ,所以选
,所以选 。
。
4.已知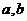 为正整数,
为正整数, ,实数
,实数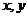 满足
满足 ,若
,若 的最大值为
的最大值为 ,则满足条件的数对
,则满足条件的数对 的数目为(
)。
的数目为(
)。
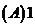
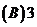
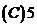
 。
。
答 选 。
。
因为 ,所以
,所以 ,
,
于是有 ,因此
,因此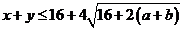 。由于
。由于 ,得
,得 ,其中
,其中 的最大值当
的最大值当 ,
,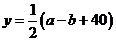 时取到。又因为
时取到。又因为 ,所以满足条件的数对
,所以满足条件的数对 的数目为
的数目为 ,选
,选 。
。
3.已知关于参数 的二次函数
的二次函数 的最小值是关于
的最小值是关于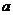 的函数
的函数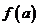 ,则
,则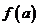 的最小值为(
)。
的最小值为(
)。
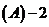


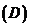 以上结果都不对
以上结果都不对
答 选 。
。
当 时,
时, 的最小值为
的最小值为 ,其中
,其中 。因为对称轴为
。因为对称轴为 ,所以当
,所以当 时
时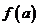 的最小值为
的最小值为 ,选
,选 。
。
2.正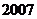 边形
边形 被它的一些不在
被它的一些不在 内部相交的对角线分割成若干个区域,每个区域都是三角形,则锐角三角形的个数为( )。
内部相交的对角线分割成若干个区域,每个区域都是三角形,则锐角三角形的个数为( )。


 大于
大于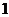
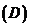 与分割的方法有关
与分割的方法有关
答 选 。
。
只有包含正 边形中心
边形中心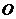 的三角形是锐角三角形,所以只有一个,选
的三角形是锐角三角形,所以只有一个,选 。
。
1.方程 的实数解的个数为( )。
的实数解的个数为( )。



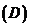 大于
大于
答 选 。
。
设 ,则
,则 ,因此
,因此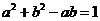 ,从而可得
,从而可得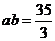 ,因此
,因此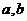 是方程
是方程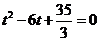 的两个实根,判别式
的两个实根,判别式 ,无解,所以选
,无解,所以选 。
。
例7. 已知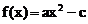 ,且
,且 ,求
,求 的范围。
的范围。
解:令
可得
∴
又
可解得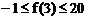
评注:题中 ,且
,且 是四个整体,在解题过程中,整体谋划,不能破坏其固有的整体结构。
是四个整体,在解题过程中,整体谋划,不能破坏其固有的整体结构。
例6. 解不等式
分析:本题若直接将左边通分采用解高次不等式的思维来做,运算较繁杂。但注意到 ,且题中出现
,且题中出现 ,启示我们构造函数
,启示我们构造函数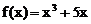 去投石问路。
去投石问路。
解:将原不等式化为
令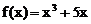
则不等式等价于
∵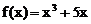 在R上为增函数
在R上为增函数
∴原不等式等价于
解得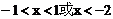
例5. 已知 ,求证
,求证
分析:结论可以转化为 ,恰好是一元二次方程有实根的必要条件。
,恰好是一元二次方程有实根的必要条件。
解:由已知可化为 ,这表明二次方程
,这表明二次方程 有实根
有实根 ,从而需要判别式
,从而需要判别式 ,即
,即 成立。
成立。
例4. 设a<0为常数,解不等式 。
。
解:不等式转化为
令函数 和
和
其图象如图所示
由
解得 (舍去)
(舍去)

∴两个函数图象的交点为
由图知,当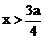 时,函数
时,函数 的图象位于函数
的图象位于函数 的图象的上方
的图象的上方
∴不等式的解集是
评注:在不等式的求解过程中,换元法和图象法是常用的技巧。通过换元,可将较复杂的不等式化归为较简单的不等式或基本不等式,通过构造函数,数形结合,则可将不等式的解化归为直观、形象的图象关系。对含有参数的不等式,运用图象法,还可以使得分类标准更加明晰。
例3. 解不等式
解:若令 则
则
∵ ,且
,且
∴
∴不等式化为
即
∴
解得
从而
即
∴不等式的解集是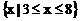
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com