6.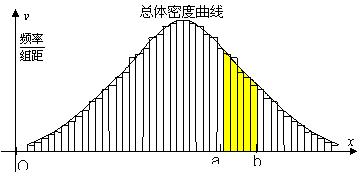总体密度曲线:如果ξ是连续型随机变量,就把ξ的取值区间分组,当样本容量无限增大，分组的组距无限缩小，各组的频率就越接近于总体在相应各组取值的概率,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线．

它反映了总体在各个范围内取值的概率．根据这条曲线，可求出总体在区间(a，b)内取值的概率等于该区间上总体密度曲线与x轴、直线x=a、x=b所围成曲边梯形的面积。

　总体分布密度密度曲线函数y=f(x)的两条基本性质：

　①f(x) ≥0(x∈R)；②由曲线y=f(x)与x轴围成面积为1。

5.总体分布：从总体中抽取一个个体，就是一次随机试验，从总体中抽取一个容量为n的样本，就是进行了n次试验，试验连同所出现的结果叫随机事件，所有这些事件的概率分布规律称为总体分布.

总体分布是不易知道的,通常用“样本频率分布估计总体分布”，这是统计的基本思想方法，样本容量越大,估计越精确.

4.频率分布：用样本估计总体，是研究统计问题的基本思想方法，样本中所有数据(或数据组)的频数和样本容量的比，就是该数据的频率.所有数据(或数据组)的频率的分布变化规律叫做样本的频率分布.可以用样本频率表、样本频率分布条形图或频率分布直方图来表示.

3.分层抽样: 当已知总体由差异明显的几部分组成时，为了使样本更充分地反映总体的情况，常将总体分成几部分，然后按照各部分所占的比例进行抽样，这种抽样叫做分层抽样，所分成的部分叫做层.

简单随机抽样,系统抽样,分层抽样都是等概率抽样,简单随机抽样是基础,系统抽样的第一部分和分层抽样的每一层都采用简单随机抽样. 随机抽样、系统抽样、分层抽样都是不放回抽样

2.系统抽样:当总体中的个体数较多时，可将总体分成均衡的几个部分，然后按预先定出的规则，从每一部分抽取一个个体，得到需要的样本，这种抽样叫做系统抽样．

系统抽样的步骤：(总体中的个体的个数为N，样本容量为n)

①采用随机的方式将总体中的个体编号.为简便起见，有时可直接采用个体所带有的号码，如考生的准考证号、街道上各户的门牌号，等等

②确定分段(部分)的间隔k当是整数时，k=;当不是整数时，先从总体中用简单随机抽样剔除一些个体,使剩下的总体中个体数能被n整除，取k=.

③在第一段用简单随机抽样确定起始的个体编号.

　　 ④按照事先确定的规则抽取样本(通常是将加上间隔k，得到第2个编号+k,第3个编号+2k，……)

与简单随机抽样一样，系统抽样是等概率抽样，它是客观的、公平的.

可以证明:当n不能整除N时,先刎除的个体与其它个体一样,被抽的概率也是1/N.

1.简单随机抽样：设一个总体的个体数为N．如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的概率相等，就称这样的抽样为简单随机抽样.

⑴简单随机抽样的特点:逐个抽取，不放回抽样,各个个体被抽到的概率相等.简单随机抽样方法是其他更复杂抽样方法的基础．

(2)简单随机抽样的两种方法:

①抽签法：编号写签,搅拌均匀，逐个抽取.先后抽取概率均等.

抽签法简便易行，适用于个体数不太多总体．

　 ②随机数表法：“三步曲”：第一步，将总体中的个体编号；第二步，选定开始的数字；第三步，获取样本号码

4.了解线性回归的方法和简单应用

3.了解正态分布的意义及主要性质

2.会用样本频率分布去估计总体分布

1.会用随机抽样、系统抽样、分层抽样等常用的抽样方法从总体中抽取样本