
2. 某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②.则完成①、②这两项调查宜采用的抽样方法依次是
A.分层抽样法,系统抽样法 B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法 D.简单随机抽样法,分层抽样法
分析:此题为抽样方法的选取问题.当总体中个体较多时宜采用系统抽样;当总体中的个体差异较大时,宜采用分层抽样;当总体中个体较少时,宜采用随机抽样.
1.一个总体中共有10个个体,用简单随机抽样的方法从中抽取一容量为3的样本,则某特定个体入样的概率是
A. B.
B.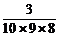 C.
C. D.
D.

4、了解线性回归的方法,会求线性回归方程。
同步练习 10.10 抽样方法 总体分布的估计
[选择题]
3、正态分布的意义、主要性质及应用;
2、用样本的频率去估计总体分布;
1、理解三种抽样方法的特点;
[例1]某批零件共160个,其中,一级品48个,二级品64个,三级品32个,等外品16个.从中抽取一个容量为20的样本.请说明分别用简单随机抽样、系统抽样和分层抽样法抽取时总体中的每个个体被取到的概率均相同.
解:(1)简单随机抽样法:可采取抽签法,将160个零件按1-160编号,相应地制作1-160号的160个签,从中随机抽20个.显然每个个体被抽到的概率为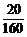 =
=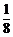 .
.
(2)系统抽样法:将160个零件从1至160编上号,按编号顺序分成20组,每组8个.然后在第1组用抽签法随机抽取一个号码,如它是第k号(1≤k≤8),则在其余组中分别抽取第k+8n(n=1,2,3,…,19)号,此时每个个体被抽到的概率为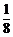 .
.
(3)分层抽样法:按比例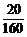 =
=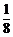 ,分别在一级品、二级品、三级品、等外品中抽取48×
,分别在一级品、二级品、三级品、等外品中抽取48×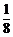 =6个,64×
=6个,64×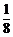 =8个,32×
=8个,32×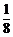 =4个,16×
=4个,16×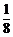 =2个,每个个体被抽到的概率分别为
=2个,每个个体被抽到的概率分别为 ,
, ,
,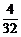 ,
,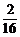 ,即都是
,即都是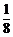 .
.
综上可知,无论采取哪种抽样,总体的每个个体被抽到的概率都是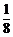 .
.
点评:三种抽样方法的共同点就是每个个体被抽到的概率相同,这样样本的抽取体现了公平性和客观性.
 [例2]设随机变量ξ的概率密度函数为
[例2]设随机变量ξ的概率密度函数为
 ,
,
求(1)常数a的值; (2)P(ξ<2)及F(x)=P(ξ<x)
解(1)f(1)=a,f(3)=0,如图,密度曲线与x轴围成三角形面积
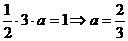 .
.
(2)f(2)= , f(ξ<2)=
, f(ξ<2)= .
.
F(x)=P(ξ<x)=

[例3]将温度调节器放置在贮存着某种液体的容器内,调节器设定在d ℃,液体的温度ξ(单位:℃)是一个随机变量,且ξ-N(d,0.52).
(1)若d=90°,求ξ<89的概率;
(2)若要保持液体的温度至少为80 ℃的概率不低于0.99,问d至少是多少?(其中若η-N(0,1),则Φ(2)=P(η<2)=0.9772,Φ(-2.327)=P(η<-2.327)=0.01).
分析:需转化为标准正态分布的数值.
解:(1)P(ξ<89)=F(89)=Φ( )=Φ(-2)=1-Φ(2)=1-0.9772=0.0228.
)=Φ(-2)=1-Φ(2)=1-0.9772=0.0228.
(2)由已知d满足0.99≤P(ξ≥80),
即1-P(ξ<80)≥1-0.01,∴P(ξ<80)≤0.01.
∴Φ(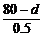 )≤0.01=Φ(-2.327).
)≤0.01=Φ(-2.327).
∴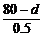 ≤-2.327. ∴d≤81.1635.
≤-2.327. ∴d≤81.1635.
故d至少为81.1635.
◆提炼方法:(1)若ξ-N(μ,σ),则η= -N(0,1).(2)标准正态分布的密度函数f(x)是偶函数,x<0时,f(x)为增函数,x>0时,f(x)为减函数.
-N(0,1).(2)标准正态分布的密度函数f(x)是偶函数,x<0时,f(x)为增函数,x>0时,f(x)为减函数.
[例4] (2006湖北)在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布N(70,100)。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)试问此次参赛的学生总数约为多少人?
(Ⅱ)若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数约为多少分?
可供查阅的(部分)标准正态分布表
|
x0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1.2 |
0.8849 |
0.8869 |
0.8888 |
0.8907 |
0.8925 |
0.8944 |
0.8962 |
0.8980 |
0.8997 |
0.9015 |
|
1.3 |
0.9032 |
0.9049 |
0.9066 |
0.9082 |
0.9099 |
0.9115 |
0.9131 |
0.9147 |
0.9162 |
0.9177 |
|
1.4 |
0.9192 |
0.9207 |
0.9222 |
0.9236 |
0.9251 |
0.9265 |
0.9278 |
0.9292 |
0.9306 |
0.9319 |
|
1.9 |
0.9713 |
0.9719 |
0.9726 |
0.9732 |
0.9738 |
0.9744 |
0.9750 |
0.9756 |
0.9762 |
0.9767 |
|
2.0 |
0.9772 |
0.9778 |
0.9783 |
0.9788 |
0.9793 |
0.9798 |
0.9803 |
0.9808 |
0.9812 |
0.9817 |
|
2.1 |
0.9821 |
0.9826 |
0.9830 |
0.9834 |
0.9838 |
0.9842 |
0.9846 |
0.9850 |
0.9854 |
0.9857 |
解:(1)设参赛学生的分布数为ξ,因为ξ-N(70,100),由条件知:

这说明成绩在90分以上(含90分)的学生人数约占全体参赛人数的2.28%
因此,参赛总人数约为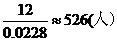
(2)假定设奖的分数线为 分,则
分,则
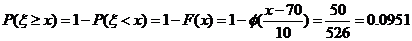
即 ,查表得
,查表得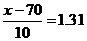 ,解得
,解得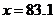
故设奖的分数线约为83分.
[研讨.欣赏] 设有一样本x1,x2,…,xn,其标准差为sx,另有一样本y1,y2,…,yn,其中yi=3xi+2(i=1,2,…,n),其标准差为sy,求证:sy=3sx.
证明:∵ =
= ,
,
∴ =
=
=
= =3
=3 +2.
+2.
∴sy2= [(y12+y22+…+yn2)-n
[(y12+y22+…+yn2)-n 2]
2]
= [(3x1+2)2+(3x2+2)2+…+(3xn+2)2-n(3
[(3x1+2)2+(3x2+2)2+…+(3xn+2)2-n(3 +2)2]
+2)2]
= [9(x12+x22+…+xn2)+12(x1+x2+…+xn)+4n-n(9
[9(x12+x22+…+xn2)+12(x1+x2+…+xn)+4n-n(9 2+12
2+12 +4)]
+4)]
= [(x12+x22+…+xn2)-n
[(x12+x22+…+xn2)-n 2]=9sx2.
2]=9sx2.
∵sx≥0,sy≥0, ∴sy=3sx.
6.先求出回归方程 =bx+a,令
=bx+a,令 =6,得x=1.5万元. 答案:1.5万元
=6,得x=1.5万元. 答案:1.5万元
5.P(-1<ξ<0)=P(0<ξ<1)=Φ(1)-Φ(0)=0.8413-0.5=0.3413.
4.根据3σ原则,在8+3×1.5=8.45,与8-3×1.5=7.55,之外时为异常.答案:C;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com