2、常量与变量

⑴、变量的定义：我们在观察某一现象的过程时，常常会遇到各种不同的量，其中有的量在过程中不起变化，我们把其称之为常量；有的量在过程中是变化的，也就是可以取不同的数值，我们则把其称之为变量。注：在过程中还有一种量，它虽然是变化的，但是它的变化相对于所研究的对象是极其微小的，我们则把它看作常量。

⑵、变量的表示：如果变量的变化是连续的，则常用区间来表示其变化范围。在数轴上来说，区间是指介于某两点之间的线段上点的全体。

区间的名称	区间的满足的不等式	区间的记号	区间在数轴上的表示
闭区间	a≤x≤b	[a，b]
开区间	a＜x＜b	(a，b)
半开区间	a＜x≤b或a≤x＜b	(a，b]或[a，b)

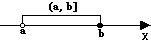
以上我们所述的都是有限区间，除此之外，还有无限区间：

[a，+∞)：表示不小于a的实数的全体，也可记为：a≤x＜+∞；

(-∞，b)：表示小于b的实数的全体，也可记为：-∞＜x＜b；

(-∞，+∞)：表示全体实数，也可记为：-∞＜x＜+∞

注：其中-∞和+∞，分别读作"负无穷大"和"正无穷大",它们不是数,仅仅是记号。

⑶、邻域：设α与δ是两个实数，且δ＞0.满足不等式│x-α│＜δ的实数x的全体称为点α的δ邻域，点α称为此邻域的中心，δ称为此邻域的半径。

5、无限集合A＝{1，2，3，4，…，n，…}，B＝{2，4，6，8，…，2n，…}，你能设计一种比较这两个集合中元素个数多少的方法吗？

4、对于有限集合A、B、C，能不能找出这三个集合中元素个数与交集、并集元素个数之间的关系呢？

3、已知集合A={x|1≤x≤3}，B＝{x|(x-1)(x-a)=0}。试判断B是不是A的子集？是否存在实数a使A＝B成立？

2、在平面直角坐标系中，集合C＝{(x,y)|y=x}表示直线y＝x，从这个角度看，集合D={(x,y)|方程组：2x-y=1,x+4y=5}表示什么？集合C、D之间有什么关系？请分别用集合语言和几何语言说明这种关系。

1、学校里开运动会，设A＝{x|x是参加一百米跑的同学}，B＝{x|x是参加二百米跑的同学}，C＝{x|x是参加四百米跑的同学}。学校规定，每个参加上述比赛的同学最多只能参加两项，请你用集合的运算说明这项规定，并解释以下集合运算的含义。⑴、A∪B；⑵、A∩B。

1、集合的概念

一般地我们把研究对象统称为元素，把一些元素组成的总体叫集合(简称集)。集合具有确定性(给定集合的元素必须是确定的)和互异性(给定集合中的元素是互不相同的)。比如“身材较高的人”不能构成集合，因为它的元素不是确定的。

我们通常用大字拉丁字母A、B、C、……表示集合，用小写拉丁字母a、b、c……表示集合中的元素。如果a是集合A中的元素，就说a属于A，记作：a∈A，否则就说a不属于A，记作：aA。

⑴、全体非负整数组成的集合叫做非负整数集(或自然数集)。记作N

⑵、所有正整数组成的集合叫做正整数集。记作N⁺或N₊。

⑶、全体整数组成的集合叫做整数集。记作Z。

⑷、全体有理数组成的集合叫做有理数集。记作Q。

⑸、全体实数组成的集合叫做实数集。记作R。

集合的表示方法

⑴、列举法：把集合的元素一一列举出来，并用“{}”括起来表示集合

⑵、描述法：用集合所有元素的共同特征来表示集合。

集合间的基本关系

⑴、子集：一般地，对于两个集合A、B，如果集合A中的任意一个元素都是集合B的元素，我们就说A、B有包含关系，称集合A为集合B的子集，记作A B(或B A)。。

⑵相等：如何集合A是集合B的子集，且集合B是集合A的子集，此时集合A中的元素与集合B中的元素完全一样，因此集合A与集合B相等，记作A＝B。

⑶、真子集：如何集合A是集合B的子集，但存在一个元素属于B但不属于A，我们称集合A是集合B的真子集。

⑷、空集：我们把不含任何元素的集合叫做空集。记作 ，并规定，空集是任何集合的子集。

⑸、由上述集合之间的基本关系，可以得到下面的结论：

①、任何一个集合是它本身的子集。即A A

②、对于集合A、B、C，如果A是B的子集，B是C的子集，则A是C的子集。

③、我们可以把相等的集合叫做“等集”，这样的话子集包括“真子集”和“等集”。

集合的基本运算

⑴、并集：一般地，由所有属于集合A或属于集合B的元素组成的集合称为A与B的并集。记作A∪B。(在求并集时，它们的公共元素在并集中只能出现一次。)

即A∪B＝{x|x∈A，或x∈B}。

⑵、交集：一般地，由所有属于集合A且属于集合B的元素组成的集合称为A与B的交集。记作A∩B。

即A∩B＝{x|x∈A，且x∈B}。

⑶、补集：

①全集：一般地，如果一个集合含有我们所研究问题中所涉及的所有元素，那么就称这个集合为全集。通常记作U。

②补集：对于一个集合A，由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集。简称为集合A的补集，记作C_UA。

即C_UA＝{x|x∈U，且x A}。

集合中元素的个数

⑴、有限集：我们把含有有限个元素的集合叫做有限集，含有无限个元素的集合叫做无限集。

⑵、用card来表示有限集中元素的个数。例如A＝{a,b,c}，则card(A)=3。

⑶、一般地，对任意两个集合A、B，有

card(A)+card(B)=card(A∪B)+card(A∩B)

我的问题：

10、函数极限的运算规则··· 11

9、函数的极限··· 9

8、数列的极限··· 8