
[例1] 在DABC中,2sinA+cosB=2,sinB+2cosA= ,则ÐC的大小应为( )
,则ÐC的大小应为( )
A. B.
B. C.
C. 或
或 D.
D. 或
或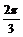
错解:C
错因:求角C有两解后未代入检验.
正解:A
[例2] 已知tana tanb是方程x2+3 x+4=0的两根,若a,bÎ(-
x+4=0的两根,若a,bÎ(-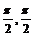 ),则a+b=( )
),则a+b=( )
A. B.
B. 或-
或- C.-
C.- 或
或 D.-
D.-
错解:B.
错因:未能准确限制角的范围.
正解:D.
[例3] △ABC中,已知cosA= ,sinB=
,sinB=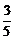 ,则cosC的值为( )
,则cosC的值为( )
A. B.
B.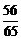 C.
C. 或
或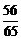 D.
D.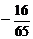
错解:C
错因:是忽略对题中隐含条件的挖掘.
正解:A
[例4] 已知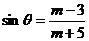 ,
,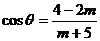 (
( ),则
),则 ( )
( )
A、 B、
B、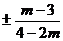 C、
C、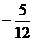 D、
D、
错解:A
错因:是忽略 ,而解不出
,而解不出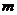
正解:C
点评:在对三角式作变形时,以上四种方法,提供了四种变形的角度,这也是研究其他三角问题时经常要用的变形手法.
6. 三角恒等式的证明包括无条件恒等式和有条件恒等式
(1)无条件恒等式证明,要认真分析等式两边三角函数的特点,角度和函数关系,找出差异寻找突破口.
(2)有条件的等式证明,常常四寻找条件与需证式的区别与联系,对条件或须证式进行变形.采用消去法或基本量法等求证.
5.化为三角函数式,常见的思路为化“三同”即同名、同角、同次,切割化弦、特殊值与特殊角的三角函数互化等.
4. 三角公式由角的拆、凑很灵活.如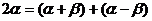 、
、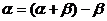 、
、
 ,
, 等,注意到倍角的相对性.
等,注意到倍角的相对性.
3.公式使用过程中(1)要注意观察差异,寻找联系,实现转化,要熟悉公式的正用逆用和变形使用,也要注意公式成立的条件.例 、
、 、
、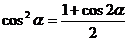 等.
等.
2.倍角公式的内涵是揭示具有倍数关系的两个角的三角函数的运算规律.如 成立的条件是“
成立的条件是“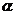 是任意角,
是任意角, 的2倍角”,精髓体现在角的“倍数”关系上.
的2倍角”,精髓体现在角的“倍数”关系上.
1.两角和与差的三角函数公式的内涵是揭示同名不同角的三角函数的运算规律,常用于解决求值、化简和证明题.
2.恒等变形主要是运用三角公式对式子进行等价变形,常见于化简求值和恒等式证明.恒等式证明就是利用公式消除等式两边的差异,有目的地化繁为简,使左右相等,常用方法为:(1)从一边开始证得它等于另一边,一般由繁到简;(2)证明左右两边都等于同一个式子(或数值).
1.两角和、差、倍、半公式
(1) 两角和与差的三角函数公式

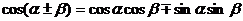

(2) 二倍角公式

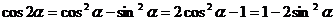
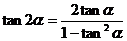
(3) 半角公式
 ,
, 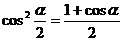 ,
,
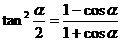
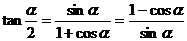
3.3三角函数的恒等变换
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com