
7.利用单调性比较函数值的大小.往往先利用对称型或周期性转化成同一单调区间上的两个同名函数.
6.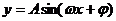
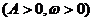 单调性的确定,基本方法是将
单调性的确定,基本方法是将 看作整体,如求增区间可由
看作整体,如求增区间可由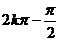



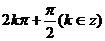 解出
解出 的范围.若
的范围.若 的系数为负数,通常先通过诱导公式处理.
的系数为负数,通常先通过诱导公式处理.
5.求三角函数的值域是常见题型.一类是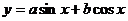 型,这要变形成
型,这要变形成 ;二是含有三角函数复合函数,可利用换元、配方等方法转换成一元二次函数在定区间上的值域.
;二是含有三角函数复合函数,可利用换元、配方等方法转换成一元二次函数在定区间上的值域.
4.三角函数的定义域是研究其它一切性质的前提.求定义域实质上是解简单的三角不等式(组).要考虑到分母不为零,偶次根式被开方数不小于零,对数的真数大于零、底数大于零且不等于1,同时还要考虑到函数本身的定义域.可用三角函数图像或三角函数线解不等式(组).
3.
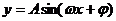 的图像既是中心对称图形,又是轴对称图形.而
的图像既是中心对称图形,又是轴对称图形.而 图像只是中心对称图形,掌握对称中心和对称轴的求法及位置特征,充分利用特征求出中
图像只是中心对称图形,掌握对称中心和对称轴的求法及位置特征,充分利用特征求出中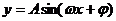
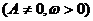 的各个参数.
的各个参数.
2.用“五点法”作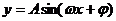
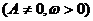 图时,将
图时,将 看作整体,取
看作整体,取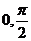 ,
,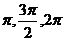 来求相应的
来求相应的 值及对应的
值及对应的 值,再描点作图.
值,再描点作图.
1.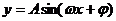 +
+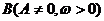 中,
中,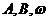 及
及 ,对正弦函数
,对正弦函数 图像的影响,应记住图像变换是对自变量而言.
图像的影响,应记住图像变换是对自变量而言.
如: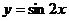 向右平移
向右平移 个单位,应得
个单位,应得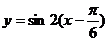 ,而不是
,而不是
4.三角函数的奇偶性和单调性
3.三角函数的定义域、值域及周期
2.三角函数的图像
(1)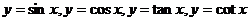 四种图像
四种图像
(2)函数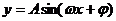 的图像
的图像
①“五点作图法”
②图像变化规律
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com