1．画出不等式－+2y－4＜0表示的平面区域.

[例1] ．画出不等式组表示的平面区域.

错解：如图(1)所示阴影部分即为不等式组表示的平面区域.

错因一是实虚线不清，二是部分不等式所表示的平面区域弄错了.

正解：如图(2)所示阴影部分即为不等式组表示的平面区域.

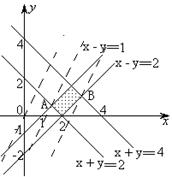[例2] 已知1x－y2,且2x+y4,求4x－2y的范围.

错解：由于　1x－y2　①,

2x+y4　　②,

①+② 得32x6　　 ③

①×(－1)+② 得：02y3　 ④.

③×2+④×(－1)得. 34x－2y12

错因：可行域范围扩大了.

正解：线性约束条件是：

令z＝4x－2y，

画出可行域如右图所示，

由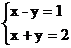得A点坐标(1.5，0.5)此时z＝4×1.5－2×0.5＝5.

由得B点坐标(3，1)此时z＝4×3－2×1＝10.

　 54x－2y10

　[例3] 已知,求x²+y²的最值.

错解：不等式组表示的平面区域如右图所示ABC的内部(包括边界)，

令z= x²+y²

由得A点坐标(4，1)，

此时z＝x²+y²＝4²+1²＝17，

由得B点坐标(－1，－6)，

此时z＝x²+y²＝(－1)²+(－6)²＝37，

由得C点坐标(－3，2)，

此时z＝x²+y²＝(－3)²+2²＝13，

　 当时x²+y²取得最大值37，当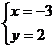时x²+y²取得最小值13.

错因：误将求可行域内的点到原点的距离的平方的最值误认为是求三点A、B、C到原点的距离的平方的最值.

正解：不等式组表示的平面区域如图所示ABC的内部(包括边界)，

令z= x²+y²,则z即为点(x，y)到原点的距离的平方.

由得A点坐标(4，1)，

此时z＝x²+y²＝4²+1²＝17，

由得B点坐标(－1，－6)，

此时z＝x²+y²＝(－1)²+(－6)²＝37，

由得C点坐标(－3，2)，

此时z＝x²+y²＝(－3)²+2²＝13，

而在原点处，，此时z＝x²+y²＝0²+0²＝0，

　 当时x²+y²取得最大值37，当时x²+y²取得最小值0.

　[例4]某家具厂有方木料90m³，五合板600m²，准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1m³，五合板2m²，生产每个书橱需要方木料0.2m³，五合板1m²，出售一张书桌可获利润80元，出售一个书橱可获利润120元.如果只安排生产书桌，可获利润多少？如果只安排生产书橱，可获利润多少？怎样安排生产可使得利润最大？

分析： 数据分析列表

设生产书桌x张，书橱y张，利润z元，则约束条件为

2x+y-600=0 　 　 A(100,400) 　　　　　　　 x+2y-900=0 　 　2x+3y=0

目标函数z=80x+120y

作出上可行域：

作出一组平行直线2x+3y=t, 此直线经过点A(100，400)时，即合理安排生产，生产书桌100张，书橱400张，有最大利润为

z_max=80×100+400×120=56000(元)

若只生产书桌，得0<x≤300，即最多生产300张书桌，利润为

z=80×300=24000(元)

若只生产书橱，得0<y≤450，即最多生产450张书橱，利润为z=120×450=54000(元)

　　 答：略

[例5]某钢材厂要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格小钢板的块数如下表：

每张钢板的面积，第一种为1m²，第二种为2 m²，今需要A、B、C三种规格的成品各12、15、27块，请你们为该厂计划一下，应该分别截这两种钢板多少张，可以得到所需的三种规格成品，而且使所用钢板的面积最小？只用第一种钢板行吗？

　 解：设需要截第一种钢板x张，第二种钢板y张，所用钢板面积为z m²，则

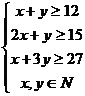　　 目标函数z=x+2y

作出可行域如图

作一组平行直线x+2y=t，

2x+y=15 　 　 　 　 　 　 x+y=12　　　 x+3y=27 　 x+2y=0

由

可得交点，

但点不是可行域内的整点，其附近的整点(4，8)或(6，7)可都使z有最小值，

且z_min=4+2×8=20 或z_min=6+2×7=20

若只截第一种钢板，由上可知x≥27，所用钢板面积最少为z=27(m²);

若只截第二种钢板，则y≥15，最少需要钢板面积z=2×15=30(m²).

它们都比z_min大，因此都不行.

答：略

　[例6]设，式中满足条件，求的最大值和最小值.

解：由引例可知：直线与所在直线平行，则由引例的解题过程知，

当与所在直线重合时最大，此时满足条件的最优解有无数多个，

当经过点时，对应最小，∴，．

说明：1．线性目标函数的最大值、最小值一般在可行域的顶点处取得；

2．线性目标函数的最值也可在可行域的边界上取得，即满足条件的最优解有无数多个.

5.简单线性规划问题就是求线性目标函数在线性约束条件下的最优解，无论此类题目是以什么实际问题提出，其求解的格式与步骤是不变的：(1)寻找线性约束条件，线性目标函数；(2)由二元一次不等式表示的平面区域做出可行域；(3)在可行域内求目标函数的最优解.

4.对于有实际背景的线性规划问题，可行域通常是位于第一象限内的一个凸多边形区域，此时变动直线的最佳位置一般通过这个凸多边形的顶点．

3. 平 移 直 线 y＝－kx +P时，直线必须经过可行域．

2.确定二元一次不等式所表示的平面区域有多种方法，常用的一种方法是“选点法”：任选一个不在直线上的点，检验它的坐标是否满足所给的不等式，若适合，则该点所在的一侧即为不等式所表示的平面区域；否则，直线的另一侧为所求的平面区域．若 直 线 不 过 原点，通 常 选 择 原 点 代入检验．

线性规划是一门研究如何使用最少的人力、物力和财力去最优地完成科学研究、工业设计、经济管理中实际问题的专门学科.主要在以下两类问题中得到应用：一是在人力、物力、财务等资源一定的条件下，如何使用它们来完成最多的任务；二是给一项任务，如何合理安排和规划，能以最少的人力、物力、资金等资源来完成该项任务.

1.对于不含边界的区域，要将边界画成虚线．

5. 整数线性规划:要求量取整数的线性规划称为整数线性规划．

4.线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值的问题，通常称为线性规划问题．只含有两个变量的简单线性规划问题可用图解法来解决．

3. 整点:坐标为整数的点叫做整点．