
17.(14分)一个袋中装有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .若袋中共有10个球,
.若袋中共有10个球,
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望E(
的数学期望E( ).
).
解 (1)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,设袋中白球的个数为x,则P(A)=1- ,
,
得到x=5,故白球有5个.
(2)随机变量 的取值为0,1,2,3,概率分布是
的取值为0,1,2,3,概率分布是
 |
0 |
1 |
2 |
3 |
|
P |
 |
 |
 |
 |
 的数学期望
的数学期望
E( )=
)=  ×0+
×0+ ×1+
×1+ ×2+
×2+ ×3=
×3=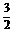 .
.
16.(14分)某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
解 (1)P= ·
· =
= .
.
(2)6场胜3场的情况有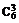 种.
种.
∴P=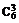
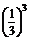
 =20×
=20× ×
× =
=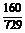 .
.
(3)由于 服从二项分布,即
服从二项分布,即 -B(6,
-B(6, ) ,
) ,
∴E( )=6×
)=6× =2,V(
=2,V( )=6×
)=6× ×(1-
×(1- )=
)=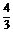 .
.
答 (1)这支篮球队首次胜场前已负两场的概率为 ;
;
(2)这支篮球队在6场比赛中恰胜3场的概率为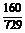 ;
;
(3)在6场比赛中这支篮球队胜场的期望为2,方差为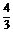 .
.
15.(14分)在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的的奖品;其余6张没有奖.某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得奖品总价值 (元)的概率分布和期望E(
(元)的概率分布和期望E( ).
).
解 方法一 (1)P=1- =1-
=1-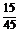 =
= .
.
即该顾客中奖的概率为 .
.
(2)  的所有可能值为:0,10,20,50,60(元).
的所有可能值为:0,10,20,50,60(元).
且P( =0)=
=0)= =
= ,P(
,P( =10)=
=10)= =
= ,
,
P( =20)=
=20)= =
= ,P(
,P( =50)=
=50)= =
= .
.
P( =60)=
=60)=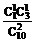 =
= .
.
故 的概率分布为:
的概率分布为:
 |
0 |
10 |
20 |
50 |
60 |
|
P |
 |
 |
 |
 |
 |
从而期望E( )=0×
)=0× +10×
+10× +20×
+20× +50×
+50× +60×
+60× =16.
=16.
方法二 (1)P= =
= =
= .
.
(2) 的概率分布求法同方法一.
的概率分布求法同方法一.
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值E( )=2×8=16(元).
)=2×8=16(元).
14.罐中有6个红球,4个白球,从中任取1球,记住颜色后再放回,连续摸取4次,设ξ为取得红球的次数,则ξ的期望E( )=
.
)=
.
答案 
13.在某项测量中,测量结果 服从正态分布N(1,
服从正态分布N(1,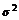 )(
)(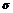 >0).若
>0).若 在(0,1)内取值的概率为0.4,则
在(0,1)内取值的概率为0.4,则 在(2,
在(2,
+∞)上取值的概率为 .
答案 0.1
12.两名战士在一次射击比赛中,战士甲得1分、2分、3分的概率分别为0.4、0.1、0.5;战士乙得1分、2分、3分的概率分别为0.1、0.6、0.3,那么两名战士得胜希望大的是 .
答案 乙
11.有一批产品,其中有12件正品和4件次品,从中任取3件,若 表示取到次品的个数,则E(
表示取到次品的个数,则E( )=
.
)=
.
答案 
10.在100张奖券中,有4张有奖,从这100张奖券中任意抽取2张,则2张都中奖的概率为 .
答案 
9.节假日时,国人发手机短信问候亲友已成为一种时尚,若小王的同事中,给其发短信问候的概率为1,0.8,0.5,0的人数分别为8,15,14,3(人),今年五一节时,通常情况下,小王应收到同事问候的短信条数为 .
答案 27
8.若 是离散型随机变量,P(
是离散型随机变量,P( =x1)=
=x1)= ,P(
,P( =x2)=
=x2)= ,且x1<x2;又已知E(
,且x1<x2;又已知E( )=
)=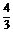 ,V(
,V( )=
)= ,则x1+x2的值为 .
,则x1+x2的值为 .
答案 3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com