
6、就--就是
(17)警方还发现这个邪教组织已经建立了自己的网站,网页上就有不少蛊惑人心的反科学的内容。
(18)你说说这样的好事,就是打着灯笼,也难找啊!
5、而--而且、从而、进而、因而、反而、而后、幸而、而况
(10)天亮后,雨不但没有停,而且越下越大了。(“而且”不能表反方向的递进,应改为“反而”)
(11)改革后,产品质量提高了,款式新颖了,而且包装也精美了,因而更加受到群众的欢迎。
(12)前年在上海见过一面,而后就不知他的去向了。(“而后”不能单用,应改为“以后”)
(13)听说老人家身体欠安,故而特来看望。(“故而”是单用词,常用于书面语中)
(14)乡党委认真贯彻执行党的政策,进而推动了生产的迅速发展。(“进而”表递进,应改为表相因相成的“从而”)
(15)我亲自感受过中国近代的屈辱史,因而对近百年来那些为中国寻求解脱之路而牺牲的先行者,一直怀有崇敬的心情。
(16)这么多事情一个人一天做完是困难的,更而况他是新手。(“而况”前不能加“更、又”)
4、为--为了、因为
(7)这些考古新发现,为人类的起源和发展提供了非常重要的依据。
(8)为了营救落水的儿童,他毫不犹豫地跳进了冰冷的河水。
(9)因为大家缺乏经验,所以前几次实验都没有成功。
3、由--由于
(5)一个人的天性不是天生的,而是由于他的家庭出身、生活环境和经历决定的。(“由于”应改为“由”)
(6)这次考试不难,但由于他准备得不够充分,差点儿就没及格。
2、及--以及、及其
(3)院子里种着大丽花、矢车菊、夹竹桃及(以及)其它的花木。
(4)不仅要掌握实词的常用义和用法,还要注意去掌握实词的运用情况及其基本规律。
1、或--或者
(1)既有丰富的知识和较强的能力,又有较高素质的人,才能称为完全的或健全的人才。
(2)这本书或者你先看,或者我先看。
0.18,所以,有且只有一条河流发生洪水的概率为:P(A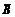 +
+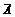 B)=P(A)P(
B)=P(A)P(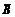 )+P(
)+P(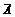 )P(B)=0.34,两河流同时发生洪水的概率为P(AB)=0.045,都不发生洪水的概率为P(
)P(B)=0.34,两河流同时发生洪水的概率为P(AB)=0.045,都不发生洪水的概率为P(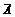
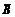 )=0.75×0.82=0.615,设损失费为随机变量ξ,
)=0.75×0.82=0.615,设损失费为随机变量ξ,
则 的概率分布为:
的概率分布为:
 |
10 000 |
60 000 |
0 |
|
P |
0.34 |
0.045 |
0.615 |
(2)对方案1来说,花费4 000元;对方案2来说,建围墙需花费1 000元,它只能抵御一条河流的洪水,但当两河流都发生洪水时,损失约56 000元,而两河流同时发生洪水的概率为P=0.25×0.18=0.045.所以,该方案中可能的花费为: 1 000+56 000×0.045=3 520(元).
对于方案3:损失费的数学期望为:
E( )=10 000×0.34+60 000×0.045=6
100(元),
)=10 000×0.34+60 000×0.045=6
100(元),
比较可知,方案2最好,方案1次之,方案3最差.
20.(16分)某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提 出以下三种方案:
方案1:运走设备,此时需花费4 000元;
方案2:建一保护围墙,需花费1 000元,但围墙只能抵御一个河流发生的洪水,当两河流同时发生洪水时,设备仍将受损,损失约56 000元;
方案3:不采取措施,此时,当两河流都发生洪水时损失达60 000元,只有一条河流发生洪水时,损失为10 000元.
(1)试求方案3中损失费 (随机变量)的概率分布;
(随机变量)的概率分布;
(2)试比较哪一种方案好.
解 (1)在方案3中,记“甲河流发生洪水”为事件A,“乙河流发生洪水”为事件B,则P(A)=0.25,P(B)=
19.(16分)某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生选修甲而不选修乙和丙的概率为0.08,选修甲和乙而不选修丙的概率是0.12,至少选修一门课的概率是0.88,用 表示该学生选修的课程门数和没有 选修的课程门数的乘积.
表示该学生选修的课程门数和没有 选修的课程门数的乘积.
(1)记“函数f(x)=x2+ ·x为R上的偶函数”为事件A,求事件A的概率;
·x为R上的偶函数”为事件A,求事件A的概率;
(2)求 的概率分布和数学期望.
的概率分布和数学期望.
解 设该学生选修甲、乙、丙的概率分别为x、y、z.
依题意得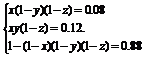
解得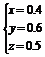
(1)若函数f(x)=x2+ ·x为R上的偶函数,则
·x为R上的偶函数,则 =0.
=0.
当 =0时,表示该学生选修三门功课或三门功课都没选.
=0时,表示该学生选修三门功课或三门功课都没选.
∴P(A)=P( =0)=xyz+(1-x)(1-y)(1-z)
=0)=xyz+(1-x)(1-y)(1-z)
=0.4×0.5×0.6+(1-0.4)(1-0.5)(1-0.6)=0.24.
∴事件A的概率为0.24.
(2)依题意知 的取值为0和2,由(1)所求可知
的取值为0和2,由(1)所求可知
P( =0)=0.24,P(
=0)=0.24,P( =2)=1-P(
=2)=1-P( =0)=0.76.
=0)=0.76.
则 的概率分布为
的概率分布为
 |
0 |
2 |
|
P |
0.24 |
0.76 |
∴ 的数学期望为E(
的数学期望为E( )=0×0.24+2×0.76=1.52.
)=0×0.24+2×0.76=1.52.
18.(2008·安徽理,19)(16分)为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物.某人一次种植了n株沙柳.各株沙柳的成活与否是相互独立的,成活率为p,设 为成活沙柳的株数,数学期望E(
为成活沙柳的株数,数学期望E( )为3,标准差
)为3,标准差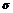 为
为 .
.
(1)求n和p的值,并写出 的概率分布;
的概率分布;
(2)若有3株或3株以上的沙柳未成活,则需要补种.求需要补种沙柳的概率.
解 由题意知, 服从二项分布B(n,p),
服从二项分布B(n,p),
P( =k)=
=k)=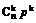 (1-p)n-k,k=0,1,…,n.
(1-p)n-k,k=0,1,…,n.
(1)由E( )=np=3,
)=np=3,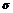 2=np(1-p)=
2=np(1-p)=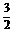 ,
,
得1-p=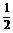 ,从而n=6,p=
,从而n=6,p=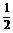 .
.
 的概率分布为
的概率分布为
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
P |
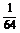 |
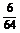 |
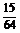 |
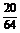 |
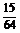 |
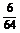 |
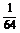 |
(2)记“需要补种沙柳”为事件A,则P(A)=P( ≤3),
≤3),
得P(A)=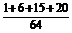 =
= ,或P(A)=1-P(
,或P(A)=1-P( >3)
>3)
=1-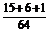 =
= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com