
41.[2010·四川文数]直线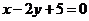 与圆
与圆 相交于A、B两点,则
相交于A、B两点,则 .
.
[答案]2
[解析]方法一、圆心为(0,0),半径为2
圆心到直线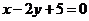 的距离为d=
的距离为d=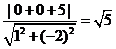
故
得|AB|=2
40.[2010·广东理数]已知圆心在x轴上,半径为 的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是 。
的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是 。
[答案]
[解析]设圆心为 ,则
,则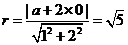 ,解得
,解得 .
.
39.[2010·天津文数]已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切。则圆C的方程为 。
[答案]
[解析]本题主要考查直线的参数方程,圆的方程及直线与圆的位置关系等基础知识,属于容易题。
令y=0得x=-1,所以直线x-y+1=0,与x轴的交点为(-1.0)
因为直线与圆相切,所以圆心到直线的距离等于半径,即 ,所以圆C的方程为
,所以圆C的方程为
[温馨提示]直线与圆的位置关系通常利用圆心到直线的距离或数形结合的方法求解。
38.[2010·四川理数]直线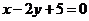 与圆
与圆 相交于A、B两点,则
相交于A、B两点,则 .
.
[ 答案]2
[解析]方法一、圆心为(0,0),半径为2
圆心到直线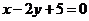 的距离为d=
的距离为d=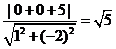
故
得|AB|=2
37.[2010·山东文数]已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l: 被该圆所截得的弦长为
被该圆所截得的弦长为 ,则圆C的标准方程为 .
,则圆C的标准方程为 .
[答案]
36. [2010·全国卷2文数]已知球
[2010·全国卷2文数]已知球 的半径为4,圆
的半径为4,圆 与圆
与圆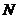 为该球的两个小圆,
为该球的两个小圆, 为圆
为圆 与圆
与圆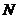 的公共弦,
的公共弦,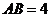 ,若
,若 ,则两圆圆心的距离
,则两圆圆心的距离 。
。
[答案]3
[解析]本题考查球、直线与圆的基础知识
∵ ON=3,球半径为4,∴小圆N的半径为 ,
,
∵小圆N中弦长AB=4,作NE垂直于AB,∴ NE= ,理可得
,理可得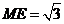 ,在直角三角形ONE中,∵
NE=
,在直角三角形ONE中,∵
NE= ,ON=3,∴
,ON=3,∴ 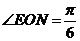 ,
,
∴  ,∴
MN=3
,∴
MN=3
35.[2010·全国卷2理数]已知球 的半径为4,圆
的半径为4,圆 与圆
与圆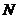 为该球的两个小圆,
为该球的两个小圆, 为圆
为圆 与圆
与圆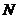 的公共弦,
的公共弦,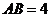 .若
.若 ,则两圆圆心的距离
,则两圆圆心的距离 .
.
[答案]3
[解析]设E为AB的中点,则O,E,M,N四点共面,如图,∵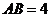 ,所以
,所以 ,∴
,∴ ,由球的截面性质,有
,由球的截面性质,有 ,∵
,∵ ,所以
,所以 与
与 全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,
全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,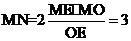
34. [2010•上海文数]圆 的圆心到直线
的圆心到直线 的距离
的距离 。
。
[答案]3
[解析]圆心(1,2)到直线 距离为
距离为
33.[2010·山东德州一模]若直线 与圆
与圆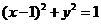 有公共点,则实数
有公共点,则实数 的取值为( )
的取值为( )
A. 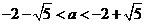 B.
B.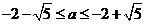
C. D.
D.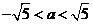
[答案]B
[解析]依题意, ,
, ,选择B
,选择B
32.[2010·锦州市年高三质量检测(二)]与直线x-y-4=0和圆x2+y2+2x-2y=0都相切的半径最小的圆的方程是( )
A. B.
B.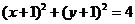
C.  D.
D. 
[答案]C
[解析]由已知圆的圆心C(-1,1)向直线x-y-4=0作垂线,垂足为H,当所求圆的圆心位于CH的上时,所求圆的半径最小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com