
9.已知a>0,b>0,c>0,且a+b+c=1.
求证:++≥9.
(文科)
8.若a、b∈R+,且满足ab=a+b+3,则ab的取值范围是__________,a+b的取值范围是__________.
7.若x≥0,y≥0,x2+=1,则x的最大值是________.
6.(2009年佛山一中月考)已知x,y∈R+,且x+4y=1,则x·y的最大值为________.
5.某工厂第一年底的产量为P,第二年的增长率为a,第三年的增长率为b,这两年的平均增长率为x,则有( )
A.x≥ B.x=
C.x≤ D.x>
4.(2010年厦门月考)已知不等式(x+y)≥9对任意正实数x,y恒成立,则正实数a的最小值为( )
A.2 B.4
C.6 D.8
3.(2008年江西卷)若0<a1<a2,0<b1<b2,且a1+a2=b1+b2=1,则下列代数式中值最大的是( )
A.a1b1+a2b2 B.a1a2+b1b2
C.a1b2+a2b1 D.
2.(2009年福州检测)若实数x,y,z满足x2+y2+z2=1,则xy+yz+zx的取值范围是( )
A.[-1,1] B.
C. D.
1.在下列函数中,最小值为2的是( )
A.y=x+
B.y=3x+3-x
C.y=lg x+(0<x<1)
D.y=sin x+
15简解:P:0<a<1;Q:a>1/2;P、Q中有且仅有一个为真∴0<a≤1/2或a≥1
16解(1)对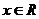 ,令x=u-v则有
,令x=u-v则有
f(-x)=f(v-u)=f(v)g(u)-g(v)f(u)=f(u-v)=-[f(u)g(v)-g(u)f(v)]=-f(x)
(2)f(2)=f{1-(-1)}=f(1)g(-1)-g(1)f(-1)=f(1)g(-1)+g(1)f(1)=f(1){g(-1)+g(1)}
∵f(2)=f(1)≠0
∴g(-1)+g(1)=1
17解:(1)若a=0,则f(x)=2x+1,f(x)的图象与x轴的交点为(-,0),满足题意.
若a≠0,则依题意得:Δ=4-4a=0,即a=1.故a=0或1.
(2)显然a≠0.
若a<0,则由x1x2=<0可知,方程f(x)=0有一正一负两根,此时满足题意.
若a>0,则Δ=0时,x=-1,不满足题意;Δ>0时,方程有两负根,也不满足题意.故a<0.
18解
(1)
 (…………4分)
(…………4分)
(2) =
=
又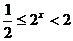 ,
, ,
, (…………………6分)
(…………………6分)
①若 ,即
,即 时,
时, =
=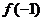 =
= ,(…………8分)
,(…………8分)
②若 ,即
,即
 时,
时,
所以当 即
即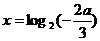 时,
时, =
= (………………11分)
(………………11分)

19解:原不等式化为<0.
(1)若1-k>0即k<1时,不等式等价于(x-)(x-2)<0.
①若k<0,不等式的解集为{x|<x<2}.
②若k=0,不等式的解集为Ø
③若0<k<1,不等式的解集为{x|2<x<}.
(2)若1-k<0即k>1时,不等式等价于(x-)(x-2)>0.此时恒有2>,所以不等式解集为{x|x<,或x>2}.
(3)若1-k=0即k=1时,不等式的解集为{x|x>2}.
综上可知当且仅当k=0时,不等式的解集为空集.
20解:(1)令m=n=1得:f(1)=2f(1),∴f(1)=0.
而f(1)=f(2·)=f(2)+f()=f(2)-1=0,
∴f(2)=1.
(2)设0<x1<x2,则>1,由已知得f()>0.∵f(1)=f(x1·)=f(x1)+f()=0,∴f()=-f(x1).
而f()=f(x2)+f(),∴f()=f(x2)-f(x1),由f()>0得f(x2)-f(x1)>0,f(x2)>f(x1),
∴f(x)在(0,+∞)上是增函数.
(3)由f(2)=1得,2=f(2)+f(2)=f(4),又f(x)≥2+f(),∴不等式化为f(x)≥f(),由(2)已证f(x)在区间(0,+∞)上是增函数可得:,
①当p>0时,由>0得x>4,∴不等式x≥可化为x2-4x-4p≥0.
这时,Δ=16+16p>0,不等式x2-4x-4p≥0的解为x≥2+2或x≤2-2.
又x>4,∴不等式组的解为x≥2+2.
②当p=0时,不等式>0不成立,∴不等式组的解集为Ø.
③当即-1<p<0时,由>0得x<4,∴不等式x≥可化为x2-4x-4p≤0.
不等式组的解为2-2≤x≤2+2.
综上可得:当p>0时,原不等式的解集是{x|x≥2+2},
当p=0时,原不等式的解集是Ø,
当-1<p<0时,原不等式的解集是{x|2-2≤x≤2+2}.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com