
2.完成下列文学常识填空。(12分)
①19世纪30年代开始, 文学成为欧洲文学的主流,长篇小说独领风骚,
的《红与黑》为其奠基, 的《人间喜剧》成为他的一座巨峰, 的《名利场》、 的《简爱》等名篇均属不朽的代表。
②现实主义作家视文学为透视 的手段,以犀利的笔锋无情揭露 ,真实再现 ,塑造了众多栩栩如生的“典型环境中的典型人物”。
③《红与黑》《高老头》《简爱》《名利场》的主人公分别是: 、 、
、 。
1.给下列加点的字注音。(8分)
悭吝( )玷污( )逶迤( )( )恪守( )狩猎( )阴霾( )乜斜( )囹圄( )( )盘桓( )蜷曲( )悄声( )后裔( )( )忖度( )
1  若a≠b,a≠0,b≠0,则
若a≠b,a≠0,b≠0,则 >
> 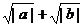

2 解不等式|x2-4x+2|≥
解不等式|x2-4x+2|≥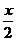

0<x≤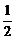 或
或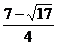 ≤x≤
≤x≤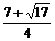 或x≥4
或x≥4
3 求证:(1)|x+1|+|x-1|≥2;
求证:(1)|x+1|+|x-1|≥2;
(2)|x+2|+|x+1|+|x-1|+|x-2|≥6;
(3)2|x+2|+|x+1|≥1(当且仅当x=-2时,“=”号成立)
证明:(1)|x+1|+|x-1|≥|(x+1)-(x-1)|=2
(2)|x+1|+|x-1|≥|(x+1)-(x-1)|=2
当且仅当(x+1)(x-1)≤0,即-1≤x≤1时“=”成立;
又|x+2|+|x-2|≥|(x+2)-(x-2)|=4,
当且仅当(x+2)(x-2)≤0,即-2≤x≤2时“=”号成立
∴|x+2|+|x+1|+|x-1|+|x-2|≥6,
当且仅当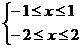 即-1≤x≤1时“=”号成立
即-1≤x≤1时“=”号成立
(3)|x+2|+|x+1|≥|(x+2)-(x+1)|=1,
当且仅当(x+2)(x+1)≤0,即-2≤x≤-1时“=”号成立;
又|x+2|≥0,当且仅当x=-2时,“=”号成立,
∴2|x+2|+|x+1|≥1,
当x=-2时,“=”号成立
4 已知f(x)=
已知f(x)=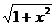 ,当|a|≠|b|时,求证:
,当|a|≠|b|时,求证:
(1)|a+b|<|f(a)+f(b)|;(2)|a-b|>|f(a)-f(b)|
证明:(1)| a+b|≤|a|+|b|<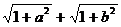 =|f(a)+f(b)|
=|f(a)+f(b)|
(2)由(1)得:|a+b|<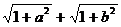 ,
,
∴|a-b|=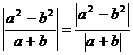
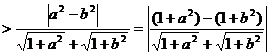
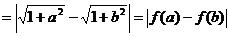
5 求证:
求证: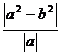 ≥|a|-|b|(a≠b)
≥|a|-|b|(a≠b)
证明:当|a|≤|b|时,|a|-|b|≤0,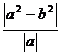 ≥0,有
≥0,有 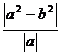 ≥|a|-|b|;
≥|a|-|b|;
当|a|>|b|时,又a≠0,从而|a|>0,有|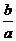 |<1
|<1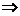 -|
-|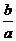 |>-1
|>-1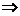 -
-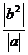 ≥-|b|
≥-|b|
∵(|b|≥0) ∴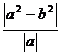 ≥
≥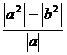 =|a|-
=|a|-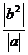 ≥|a|-|b|
≥|a|-|b|
综上所述有: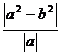 ≥|a|-|b|(a≠b)
≥|a|-|b|(a≠b)
6 若|x|<1,|y|<1,|z|<1,求证:|
若|x|<1,|y|<1,|z|<1,求证:|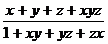 |<1
|<1
证明:所证不等式
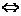 |x+y+z+xyz|<|1+xy+yz+zx|
|x+y+z+xyz|<|1+xy+yz+zx|
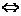 (x+y+z+xyz)2<(1+xy+yz+zx)2
(x+y+z+xyz)2<(1+xy+yz+zx)2
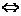 (xyz+xy+yz+zx+x+y+z+1)(xyz-xy-yz-zx+x+y+z-1)<0
(xyz+xy+yz+zx+x+y+z+1)(xyz-xy-yz-zx+x+y+z-1)<0
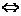 [(x+1)(y+1)(z+1)]·[(x-1)(y-1)(z-1)]<0
[(x+1)(y+1)(z+1)]·[(x-1)(y-1)(z-1)]<0
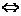 (x2-1)(y2-1)(z2-1)<0
(x2-1)(y2-1)(z2-1)<0
由于|x|<1,|y|<1,|z|<1,从而x2<1,y2<1,z2<1,
于是(x2-1)(y2-1)(z2-1)<0成立,所以原不等式成立
7 已知a,b∈R,求证:
已知a,b∈R,求证: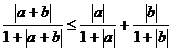

证明:原不等式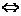 |a+b|(1+|a|)(1+|b|)
|a+b|(1+|a|)(1+|b|)
≤|a|(1+|a+b|)(1+|b|)+|b|(1+|a+b|)(1+|a|)
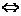 |a+b|(1+|b|)+|a+b|·|a|(1+|b|)
|a+b|(1+|b|)+|a+b|·|a|(1+|b|)
≤|a|(1+|b|)+|a|·(1+|b|)·|a+b|+|b|(1+|a|)+|b|·|a+b|(1+|a|)
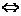 |a+b|+|a+b|·|b|≤|a|+2|ab|+|b|+|b|·|a+b|+|ab|·|a+b|
|a+b|+|a+b|·|b|≤|a|+2|ab|+|b|+|b|·|a+b|+|ab|·|a+b|
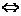 |a+b|≤|a|+|b|+2|ab|+|ab|·|a+b|
|a+b|≤|a|+|b|+2|ab|+|ab|·|a+b|
由于|a+b|≤|a|+|b|成立,显然最后一个不等式成立,从而原不等式成立
以上证明是最基本的方法,但过程繁琐冗长,利用放大技巧证明要简捷得多,证明如下:
∵|a+b|≤|a|+|b|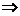 |a|+|b|-|a+b|≥0,
|a|+|b|-|a+b|≥0,
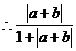
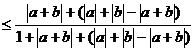
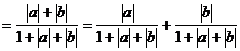
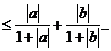
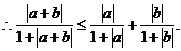
2.已知函数f(x)=-2x+1,对任意的正数ε,使得|f(x1)-f(x2)|<ε成立的一个充分非必要条件是( C )
A |x1-x2|<ε B
|x1-x2|<ε B |x1-x2|<
|x1-x2|<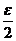 C
C |x1-x2|<
|x1-x2|<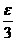 D
D |x1-x2|>
|x1-x2|>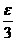
1.若|x-a|<m,|y-a|<n,则下列不等式一定成立的是( D )
A |x-y|<2m B
|x-y|<2m B |x-y|<2n C
|x-y|<2n C |x-y|<n-m
D
|x-y|<n-m
D |x-y|<n+m
|x-y|<n+m
例1 已知a、b、c、d都是实数,且a2+b2=r2,c2+d2=R2,(r>0,R>0)
求证:|ac+bd|≤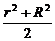

证明:(综合法)∵a、b、c、d都是实数,
∴|ac+bd|≤|ac|+|bd|≤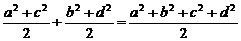
∵a2+b2=r2,c2+d2=R2,
∴|ac+bd|≤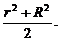

例2 设f
(x) = x2+px+q, 求证:|
f (1) |、| f (2) |、| f (3) | 中至少有一个不小于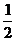

说明:此题正面证明较为困难,“正难则反”,引导学生尝试“反证法”证明
证明:(反证法)假设原命题不成立,则|f(1)|<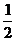 ,|f(2)|<
,|f(2)|<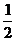 ,|f(3)|<
,|f(3)|<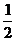 ,
,
∴ |f(1)|+2 |f(2)|+|f(3)|<2 ①
由f(1)=1+p+q, f(2)=4+2p+q, f(3)=9+3p+q 得
f(1)+f(3)-2f(2)=2
∴ |f(1)|+2 |f(2)|+|f(3)|≥|f(1)+f(3)-2f(2)|=2
这与①矛盾,故假设不成立,求证为真
例3 求证:

证法一:(分析法)要证明
只需证 (|a|+|b|)(1+|a+b|)≥|a+b| (1+|a|+|b|)
只需证 |a|+|b|+(|a|+|b|)·|a+b|≥|a+b|+(|a|+|b|)|a+b|
只需证|a|+|b|≥|a+b|
显然上式成立
所以原不等式成立
证法二:(利用函数的单调性)
构造函数f(x)=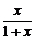 (x≥0)
(x≥0)
∵f(x)= 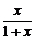 =1-
=1-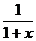
∴函数f(x)在[0,+∞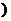 是增函数
是增函数
∵f(|a|+|b|)=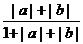 , f(|a+b|)=
, f(|a+b|)=
而 |a|+|b|≥|a+b|,∴f(|a|+|b|)≥f(|a+b|)
即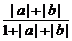 ≥
≥
例4 已知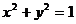 ,求证:
,求证: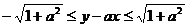
说明:根据已知条件x2+y2=1的形式特点,可以进行三角代换,即设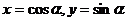 ,转化为三角形式的不等式
,转化为三角形式的不等式
解:设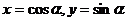 , 则
, 则
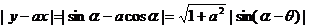 (其中tanθ=a)
(其中tanθ=a)
∵|sin(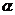 -θ)|≤1
-θ)|≤1
∴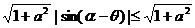
∴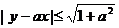
即 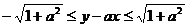
上一节课,我们学习了含绝对值的不等式的一个重要性质,并认识到证明不等式的方法的多样性与灵活性,这一节,我们将综合运用绝对值的性质、不等式的性质、算术平均数与几何平均数的定理证明不等式
定理: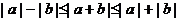
注意:1° 左边可以“加强”同样成立,即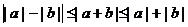
2° 这个不等式俗称“三角不等式”-三角形中两边之和大于第三边,两边之差小于第三边
3° a,b同号时右边取“=”,a,b异号时左边取“=”
推论1: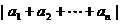 ≤
≤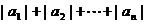
推论2: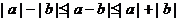
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com