
3.已知甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量 和
和 ,已知
,已知 和
和  的分布列如下:(注得分越大,水平越高)
的分布列如下:(注得分越大,水平越高)
 |
1 |
2 |
3 |
|
p |
a |
0.1 |
0.6 |
 |
1 |
2 |
3 |
|
p |
0.3 |
b |
0.3 |
试分析甲、乙技术状况
解:由0.1+0.6+a+1 a=0.3
a=0.3
2.已知随机变量 服从二项分布即
服从二项分布即 ~B(6、
~B(6、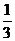 )求b (2;6,
)求b (2;6,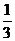 )
)
解:p( =2)=c62(
=2)=c62(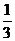 )2(
)2( )4
)4
1.设 -B(n、p)且E
-B(n、p)且E =12 D
=12 D =4,求n、p
=4,求n、p
解:由二次分布的期望与方差性质可知E =np
D
=np
D = np(1-p)
= np(1-p)
∴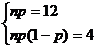 ∴
∴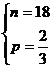
⑵对于两个随机变量 和
和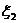 ,在
,在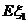 和
和 相等或很接近时,比较
相等或很接近时,比较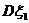 和
和
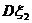 ,可以确定哪个随机变量的性质更适合生产生活实际,适合人们的需要
,可以确定哪个随机变量的性质更适合生产生活实际,适合人们的需要
6. 在有奖摸彩中,一期(发行10000张彩票为一期)有200个奖品是5元的,20个奖品是25元的,5个奖品是100元的.在不考虑获利的前提下,一张彩票的合理价格是多少元?
分析:这是同学们身边常遇到的现实问题,比如福利彩票、足球彩票、奥运彩票等等.一般来说,出台各种彩票,政府要从中收取一部分资金用于公共福利事业,同时也要考虑工作人员的工资等问题.本题的“不考虑获利”的意思是指:所收资金全部用于奖品方面的费用
解:设一张彩票中奖额为随机变量ξ,显然ξ所有可能取的值为0,5,25,100 依题
依题
意,可得ξ的分布列为
|
ξ |
0 |
5 |
25 |
100 |
|
P |
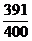 |
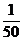 |
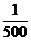 |
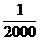 |
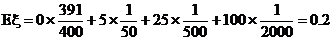
答:一张彩票的合理价格是0.2元.
5. 有A、B两种钢筋,从中取等量样品检查它们的抗拉强度,指标如下:
|
ξA |
110 |
120 |
125 |
130 |
135 |
|
ξB |
100 |
115 |
125 |
130 |
145 |
|
P |
0.1 |
0.2 |
0.4 |
0.1 |
0.2 |
|
P |
0.1 |
0.2 |
0.4 |
0.1 |
0.2 |
其中ξA、ξB分别表示A、B两种钢筋的抗拉强度.在使用时要求钢筋的抗拉强度不低于120,试比较A、B两种钢筋哪一种质量较好
分析: 两个随机变量ξA和ξB&都以相同的概率0.1,0.2,0.4,0.1,0.2取5个不同的数值.ξA取较为集中的数值110,120,125,130,135;ξB取较为分散的数值100,115,125,130,145.直观上看,猜想A种钢筋质量较好.但猜想不一定正确,需要通过计算来证明我们猜想的正确性
解:先比较ξA与ξB的期望值,因为
EξA=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
EξB=100×0.1+115×0.2+125×0.4十130×0.1+145×0.2=125.
所以,它们的期望相同.再比较它们的方差.因为
DξA=(110-125)2×0.1+(120-125) 2 ×0.2+(130-125) 2×0.1+(135-125) 2×0.2=50,
DξB=(100-125)2×0.1+(110-125) 2 ×0.2+(130-125) 2×0.1+(145-125) 2×0.2=165.
所以,DξA < DξB.因此,A种钢筋质量较好
4. 设事件A发生的概率为p,证明事件A在一次试验中发生次数ξ的方差不超过1/4
分析:这是一道纯数学问题.要求学生熟悉随机变量的期望与方差的计算方法,关键还是掌握随机变量的分布列.求出方差Dξ=P(1-P)后,我们知道Dξ是关于P(P≥0)的二次函数,这里可用配方法,也可用重要不等式证明结论
证明:因为ξ所有可能取的值为0,1且P(ξ=0)=1-p,P(ξ=1)=p,
所以,Eξ=0×(1-p)+1×p=p 
则 Dξ=(0-p)2×(1-p)+(1-p)
2×p=p(1-p) 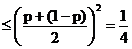
3. 有一批数量很大的商品的次品率为1%,从中任意地连续取出200件商品,设其中次品数为ξ,求Eξ,Dξ
分析:涉及产品数量很大,而且抽查次数又相对较少的产品抽查问题.由于产品数量很大,因而抽样时抽出次品与否对后面的抽样的次品率影响很小,所以可以认为各次抽查的结果是彼此独立的.解答本题,关键是理解清楚:抽200件商品可以看作200次独立重复试验,即ξ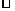 B(200,1%),从而可用公式:Eξ=np,Dξ=npq(这里q=1-p)直接进行计算
B(200,1%),从而可用公式:Eξ=np,Dξ=npq(这里q=1-p)直接进行计算
解:因为商品数量相当大,抽200件商品可以看作200次独立重复试验,所以ξ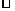 B(200,1%)
B(200,1%) 因为Eξ=np,Dξ=npq,这里n=200,p=1%,q=99%,所以,Eξ=200×1%=2,Dξ=200×1%×99%=1.98
因为Eξ=np,Dξ=npq,这里n=200,p=1%,q=99%,所以,Eξ=200×1%=2,Dξ=200×1%×99%=1.98
2. 一盒中装有零件12个,其中有9个正品,3个次品,从中任取一个,如果每次取出次品就不再放回去,再取一个零件,直到取得正品为止.求在取得正品之前已取出次品数的期望.
分析:涉及次品率;抽样是否放回的问题.本例采用不放回抽样,每次抽样后次品率将会发生变化,即各次抽样是不独立的.如果抽样采用放回抽样,则各次抽样的次品率不变,各次抽样是否抽出次品是完全独立的事件.
解:设取得正品之前已取出的次品数为ξ,显然ξ所有可能取的值为0,1,2,3
当ξ=0时,即第一次取得正品,试验停止,则
P(ξ=0)=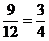
当ξ=1时,即第一次取出次品,第二次取得正品,试验停止,则
P(ξ=1)=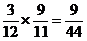
当ξ=2时,即第一、二次取出次品,第三次取得正品,试验停止,则
P(ξ=2)=
当ξ=3时,即第一、二、三次取出次品,第四次取得正品,试验停止,则P(ξ=3)=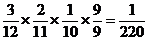
所以,Eξ=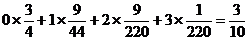

1.已知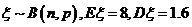 ,则
,则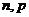 的值分别是(
)
的值分别是(
)
A.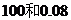 ; B.
; B.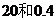 ; C.
; C. ; D.
; D.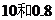

答案:1.D 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com