9．(2009年襄樊市)如图1所示的杠杆中，属于费力杠杆的是C

8．(2009年德州市)如图2所示的杠杆处于平衡状态，若使弹黄秤的示数变为原来的1/2，杠杆仍然保持平衡状态，可以采取哪些措施？ D

A、把弹簧秤向左移动一个小格

B、减少三个钩码

C、把钩码向左移动一个小格

D、把钩码向右移动一个小格

7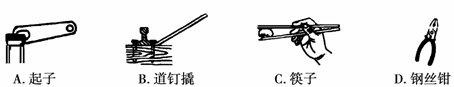．(2009年娄底市)简单机械在日常生活中应用十分广泛，下列图中属于费力杠杆的C

6．(09年南昌市)如图14所示,是2008北京残奥会开幕式最后一棒火炬手侯斌，靠自己双手的力量，攀爬到火炬台底部并最终点燃圣火的照片，该点火仪式充分体现了残疾人自强自立、拼搏向上的勇气和精神.已知他和轮椅总质量为80kg，攀爬高度39m，历时约3min20s.

(1)如果不计机械装置的额外功，求他的平均功率多大？

(2)小明同学看到火炬手攀爬很费劲，想到物理课上学过利用滑轮组可

以省力.小明同学如果站在地面上,用如图15所示的哪个滑轮组拉起火炬

手侯斌最合适,理由是什么?如果该滑轮组机械效率为80%，求小明同学

的拉力至少要多大？(g取10N/kg)

　答案.解：(1)P＝W/t＝Gh/t＝mgh/t＝80㎏×10N/㎏×39m/200s＝156W………… (3分)

(2)D滑轮组. 拉力方向向下且更省力 …………………(2分)

∵η＝W_有用/W_总＝Gh/Fs＝Gh/4Fh＝G/4F

∴F＝G/4η＝(80kg×10N/㎏)/(4×0.8)＝250N… ……………………(3分)

评分意见：有其它合理答案均参照给分.

5．(09常德)用如图所示滑轮组将一物体匀速提高2m，已知拉力大小恒为60N，

方向总保持竖直向上，动滑轮的质量为3kg，绳重和摩擦均不计。求：

(1)物体所受重力；

(2)该滑轮组在此过程中的机械效率(保留1位小数)。

4．(09常德)下列工具：①钢丝钳　 ②钓鱼杆　 ③筷子　 ④镊子　 ⑤开酒瓶用的起子，其中属于费力杠杆的是B

A．①②③　 　B．②③④　 　C．①③⑤　 　D．②③⑤

3．．(09福州)用滑轮组将一个重为5N的物体匀速提升10cm，由图9可知，绳端受到的拉力F为　 　　　N，绳端移动的距离s为　 　　　cm，滑轮组的机械效率η为　 　　　 。

答案：2N　　 30　　　 83%

2．(09福州)如图3所示，使用中属于费力杠杆的工具是C

1、(2009年贵阳市)如图19所示，拉力F=80N，物体重G=120N，若绳子自由端匀速拉动的距离s=4m，物体被提高的距离h=2m，，求：

(1)拉力所做的有用功；

(2)拉力所做的总功W_总；

(3)该滑轮组的机械效率η。

解：⑴W_有=Gh=120N×2m=240J　　　　　　　　　　 (2分)

　　　　 ⑵W_总=FS=80N×4m=320J　　　　　　　　　 (2分)　　　　

⑶×100%=×100%=75%　　　　 (2分)

20．(天津19)(本小题满分12分)

如图，在五面体ABCDEF中，FA 平面ABCD, AD//BC//FE，ABAD，M为EC的中点，AF=AB=BC=FE=AD　　　

(I)　 求异面直线BF与DE所成的角的大小；

(II)　 证明平面AMD平面CDE；

(III)求二面角A-CD-E的余弦值。　　

本小题要考查异面直线所成的角、平面与平面垂直、二面角等基础知识，考查用空间向量解决立体几何问题的方法，考查空间想像能力、运算能力和推理论证能力。满分12分.

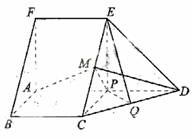方法一：(Ⅰ)解：由题设知，BF//CE，所以∠CED(或其补角)为异面直线BF与DE所成的角。设P为AD的中点，连结EP，PC。因为FEAP，所以FAEP，同理ABPC。又FA⊥平面ABCD，所以EP⊥平面ABCD。而PC，AD都在平面ABCD内,故EP⊥PC，EP⊥AD。由AB⊥AD，可得PC⊥AD设FA=a，则EP=PC=PD=a,CD=DE=EC=，故∠CED=60°。所以异面直线BF与DE所成的角的大小为60°　　

(II)证明：因为

(III)

由(I)可得，

方法二：如图所示，建立空间直角坐标系，

点为坐标原点。设依题意得　 　　

(I)　 　　　

所以异面直线与所成的角的大小为.

(II)证明： 　，

(III)　　

又由题设，平面的一个法向量为