
(15) 设数列{an}的首项a1=a≠ ,且
,且 ,
,
记 ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求
(16) 数列{an}的前n项和为Sn,且a1=1, ,n=1,2,3,……,求
,n=1,2,3,……,求
(I)a2,a3,a4的值及数列{an}的通项公式;
(II) 的值.
的值.
(17) 已知{ }是公比为q的等比数列,且
}是公比为q的等比数列,且 成等差数列.
成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{ }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
.
(18) 已知定义在R上的函数 和数列
和数列 满足下列条件:
满足下列条件:
 ,
,
 ,其中a为常数,k为非零常数.
,其中a为常数,k为非零常数.
(Ⅰ)令
 ,证明数列
,证明数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)当 时,求
时,求 .
.
(11) 在等差数列{an}中,a1>0,a5=3a7,前n项和为Sn,若Sn取得最大值,则n= .
(12) 在等差数列{an}中,前n项和为Sn,若S19=31,S31=19,则S50的值是______
(13)在等比数列{an}中,若a9·a11=4,则数列{ }前19项之和为_______
}前19项之和为_______
(14)若a>0,且a≠1, 则
 的值是
.
的值是
.
(1) 已知等差数列{an}的前n项和为Sn,且S4=3,S8=7,则S12的值是 ( )
A 8 B 11 C 12 D 15
(2) 已知数列 满足
满足 ,则
,则 = ( )
= ( )
A 0 B  C
C  D
D 
(3) 数列1,(1+2),(1+2+22),…,( 1+2+22+…+2n-1+…)的前n项和是 ( )
A 2n B 2n-2 C 2n+1- n -2 D n·2n
(4) 从集合{1,2,3,4,5,6,7,8,9,10}中任选三个不同的数,如果这三个数经过适当的排列成等差数列,则这样的等差数列一共有 ( )
A 20个 B 40个 C 10个 D 120个
(5) 
 =
( )
=
( )
A 2
B 4 C  D
0
D
0
(6) 如果 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差 ,则
( )
,则
( )
A  B
B  C
C  D
D 
(7)已知等差数列{an}与{bn}的前n项和分别为Sn与Tn, 若 , 则
, 则
 的值是
( )
的值是
( )
A  B
B  C
C  D
D 
(8) 
 的值是
(
)
的值是
(
)
A  B
B
 C
C
 D
D 
(9) 已知数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a2=5,则
 =
(
)
=
(
)
A 2 B  C 1 D
C 1 D 
(10) 已知数列 满足
满足 ,
, ,
, ….若
….若 ,则 ( )
,则 ( )
A  B3
C4
D5
B3
C4
D5
22.(本小题12分)若函数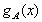 的定义域为
的定义域为 ,且
,且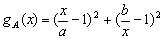 ,
, 且
且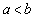 .
.
(1)求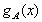 的最小值;
的最小值;
(2)求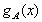 的单调区间;
的单调区间;
(3)若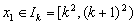 ,
, ,
,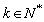 ,求证:
,求证: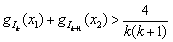 .
.
21.(本小题12分)若存在实常数 和
和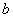 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和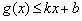 ,则称直线
,则称直线 为函数
为函数 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, .
.
(1)求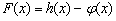 的极值;
的极值;
(2)函数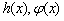 是否存在隔离直线.
是否存在隔离直线.
20.(本小题12分)已知某企业原有员工2000人,每人每年可为企业创利润 万元,为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的
万元,为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的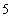 %,并且每年给每位待岗员工发放生活补贴0.5万元.据评估,当待岗员工人数
%,并且每年给每位待岗员工发放生活补贴0.5万元.据评估,当待岗员工人数 不超过原有员工的1%时,留岗员工每人每年可为企业多创利润(
不超过原有员工的1%时,留岗员工每人每年可为企业多创利润( )万元;当待岗员工人数
)万元;当待岗员工人数 超过原有员工的1%时,留岗员工每人每年可为企业多创利润0.9595万元.为使企业年利润最大,应安排多少员工待岗?
超过原有员工的1%时,留岗员工每人每年可为企业多创利润0.9595万元.为使企业年利润最大,应安排多少员工待岗?
19.(本小题12分)已知函数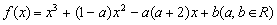 .
.
(1)若函数 的图象过原点,且在原点处的切线的斜率是
的图象过原点,且在原点处的切线的斜率是 ,求
,求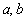 的值;
的值;
(2)若函数 在区间
在区间 上不单调,求
上不单调,求 的取值范围.
的取值范围.
18.(本小题12分)已知实数 满足
满足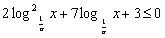 ,求函数
,求函数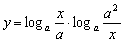 的最大值和最小值.
的最大值和最小值.
17.(本小题10分)已知二次函数 满足:①在
满足:①在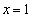 时有极值;②图象过点
时有极值;②图象过点 ,且在该点处的切线与直线
,且在该点处的切线与直线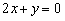 平行.
平行.
(1)求 的解析式;
的解析式;
(2)若曲线 上任意两点的连线的斜率恒大于
上任意两点的连线的斜率恒大于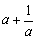 ,求
,求 的取值范围.
的取值范围.
16.已知两个实数 ,满足
,满足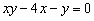 ,则
,则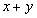 的取值范围为_____________
的取值范围为_____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com