
9、如图所示为一列简谐横波t=0.1秒时刻的波动图象,已知波沿x轴正方向传播,波速大小为0.4m/s。则 ( )
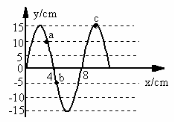 A.此时刻,质点a、b所受的回复力大小之比为2:1
A.此时刻,质点a、b所受的回复力大小之比为2:1
B.质点a比质点c要先回到平衡位置
C.在标明的三个质点中,质点c的振幅最大
D.在0.72秒时刻,质点c的振动方向向上
8、在欢庆节日的时候,人们会在夜晚燃放美丽的焰火.按照设计,某种型号的装有焰火的礼花弹从专用炮筒中射出后,在4s末到达离地面100m的最高点时炸开,构成各种美丽的图案.假设礼花弹从炮筒中射出时的初速度是v0,上升过程中所受的平均阻力大小始终是自身重力的k倍,那么v0和k分别等于(重力加速度g取10m/s2) ( )
A. 25m/s,1.25 B. 40m/s,0.25 C. 50m/s,0.25 D. 80m/s,1.25
7.我国古代神话传说中有:地上的“凡人”过一年,天上的“神仙”过一天.如果把看到一次日出就当作一天,那么,近地面轨道(距离地面300-700km)环绕地球飞行的宇航员24 h内在太空中度过的“天”数约为 (地球半径R=6400km,重力加速度g=10m/s2) ( )
A.24 B.16 C.8 D.1
6.质量为m1的物体放在A地的地面上,用竖直向上的力F拉物体,物体在竖直方向运动时产生的加速度与拉力的关系如图中A线所示;质量为m2的物体在B地地面上做类似的实验,得到加速度与拉力关系如图中B线所示,A、B两线的延长线交Oa轴于同一点,设A、 B两地的重力加速度分别为g1和g2,由图可知 (
)
B两地的重力加速度分别为g1和g2,由图可知 (
)
A. B.
B.
C. D.
D.
5、如图所示,在一次空地演习中,离地H高处的飞机以水平速度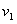 发射一颗炮弹欲轰炸
地面目标P,反应灵敏的地面拦截系统同时以速度
发射一颗炮弹欲轰炸
地面目标P,反应灵敏的地面拦截系统同时以速度 竖直向上发射炮弹拦截,设拦截系统
竖直向上发射炮弹拦截,设拦截系统 与飞机的水平距离为
与飞机的水平距离为 ,若拦截成功,不计空气阻力,则
,若拦截成功,不计空气阻力,则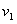 、
、 的关系应满足( )
的关系应满足( )
A.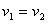 B.
B.
C.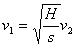 D.
D.
4.如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管往下滑。已知这名消防队员的质量为60kg,他从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零。如果他加速时的加速度大小是减速时的2倍,下滑的总时间为 3s,g取10m/s2,那么该消防队员
(
)
3s,g取10m/s2,那么该消防队员
(
)
A.下滑过程中的最大速度为8 m/s
B.加速与减速过程的时间之比为1:3
C.加速与减速过程中所受摩擦力大小之比为1:3
D.加速与减速过程的位移之比为1:4
3. 在军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达最大值v1时打开降落伞,做减速运动,在t2时刻以较小速度v2着地。他的速度图象如图所示。下列关于该空降兵在0-t1或t1-t2时间内的的平均速度 的结论正确的是( )
的结论正确的是( )
A.0-t1, B.t1-t2,
B.t1-t2,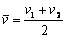
C.t1-t2, 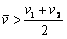 D.t1-t2,
D.t1-t2,
2.如图所示,质量为m的质点静止地放在半径为R的半球体上,质点与半球体间的动摩擦因数为 ,质点与球心的连线与水平地面的夹角为
,质点与球心的连线与水平地面的夹角为 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.地面对半球体的摩擦力方向水平向左
 B.质点对半球体的压力大小为mgcos
B.质点对半球体的压力大小为mgcos
C.质点所受摩擦力大小为mgsin
 D.质点所受摩擦力大小为mgcos
D.质点所受摩擦力大小为mgcos
1.匀强磁场中有一个静止的氡原子核( ),由于衰变它放 出一个粒子,此粒子的径迹与反冲核的径迹是两个相互外切的圆,大圆与小圆的直径之比为42 : 1,如图所示。那么氡
),由于衰变它放 出一个粒子,此粒子的径迹与反冲核的径迹是两个相互外切的圆,大圆与小圆的直径之比为42 : 1,如图所示。那么氡 核的衰变方程应是下列方程的哪一个 (
)
核的衰变方程应是下列方程的哪一个 (
)
A. →
→
B. →
→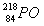 +
+
C. →
→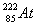 +
+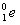
D. →
→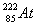 +
+
22、解:(Ⅰ)当 时,
时, ,
, ;………2分
;………2分
对于 [1,e],有
[1,e],有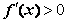 ,∴
,∴ 在区间[1,e]上为增函数,…3分
在区间[1,e]上为增函数,…3分
∴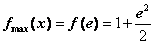 ,
, .……………………………5分
.……………………………5分
(Ⅱ)令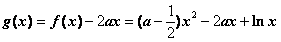 ,
,
则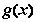 的定义域为(0,+∞).…………6分
的定义域为(0,+∞).…………6分
在区间(1,+∞)上函数 的图象恒在直线
的图象恒在直线 下方等价于
下方等价于 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立.
∵
① 若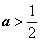 ,令
,令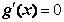 ,得极值点
,得极值点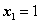 ,
,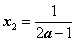 ,
,
当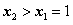 ,即
,即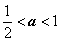 时,在(
时,在(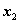 ,+∞)上有
,+∞)上有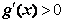 ,
,
此时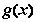 在区间(
在区间(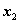 ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有
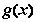 ∈(
∈( ,+∞),不合题意;………………………………………8分
,+∞),不合题意;………………………………………8分
当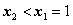 ,即
,即 时,同理可知,
时,同理可知,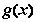 在区间(1,+∞)上,有
在区间(1,+∞)上,有
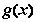 ∈(
∈( ,+∞),也不合题意;………………………………………9分
,+∞),也不合题意;………………………………………9分
② 若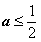 ,则有
,则有 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有 ,
,
从而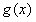 在区间(1,+∞)上是减函数;……………………………………10分
在区间(1,+∞)上是减函数;……………………………………10分
要使 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
 ,
,
由此求得 的范围是[
的范围是[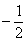 ,
,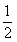 ].
].
综合①②可知,当 ∈[
∈[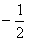 ,
, ]时,
]时,
函数 的图象恒在直线
的图象恒在直线 下方. ………………12分
下方. ………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com