
6. 已知 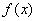 是一次函数,其图象过点
是一次函数,其图象过点  ,又
,又  成等差数列,求
成等差数列,求 的值.
的值.
4.在△ABC中,三边 成等差数列,
成等差数列,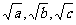 也成等差数列,求证△ABC为正三角形。 5. 三数成等比数列,若将第三个数减去32,则成等差数列,若再将这等差数列的第二个数减去4,则又成等比数列,求原来三个数。
也成等差数列,求证△ABC为正三角形。 5. 三数成等比数列,若将第三个数减去32,则成等差数列,若再将这等差数列的第二个数减去4,则又成等比数列,求原来三个数。
3.已知数列 中,
中, 是它的前
是它的前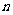 项和,并且
项和,并且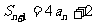 ,
,
(1) 设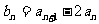 ,求证数列
,求证数列 是等比数列;
是等比数列;
(2) 设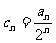 ,求证数列
,求证数列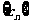 是等差数列。
是等差数列。
2.某城市1991年底人口为500万,人均住房面积为6 m2,如果该城市每年人口平均增长率为1%,每年平均新增住房面积为30万m2,求2000年底该城市人均住房面积为多少m2?(精确到0.01)
1.在[1000,2000]内能被3整除且被4除余1的整数有多少个?
[例1]设 是由正数组成的等比数列,Sn是其前n项和.证明:
是由正数组成的等比数列,Sn是其前n项和.证明: 。
。
错解:欲证
只需证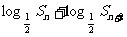 >2
>2
即证: >
>
由对数函数的单调性,只需证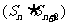 <
<

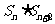 -
- =
=
=-
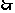
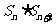 <
<
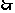 原不等式成立.
原不等式成立.
错因:在利用等比数列前n项和公式时,忽视了q=1的情况.
正解:欲证
只需证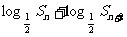 >2
>2
即证: >
>
由对数函数的单调性,只需证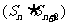 <
<
由已知数列 是由正数组成的等比数列,
是由正数组成的等比数列,
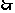
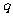 >0,
>0, .
.
若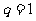 ,
,
则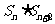 -
- =
= =-
=-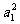 <0;
<0;
若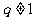 ,
,
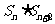 -
- =
=
=-
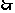
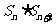 <
<
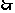 原不等式成立.
原不等式成立.
[例2] 一个球从100米高处自由落下,每次着地后又跳回至原高度的一半落下,当它第10次着地时,共经过了多少米?(精确到1米)
错解:因球 每次着地后又跳回至原高度的一半,从而每次着地之间经过的路程形成了一公比为 的等比数列,又第一次着地时经过了100米,故当它第10次着地时,共经过的路程应为前10项之和.
的等比数列,又第一次着地时经过了100米,故当它第10次着地时,共经过的路程应为前10项之和.
即 =199(米)
=199(米)
错因:忽视了球落地一次的路程有往有返的情况.
正解:球第一次着地时经过了100米,从这时到球第二次着地时,一上一下共经过了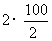 =100(米)…因此到球第10次着地时共经过的路程为
=100(米)…因此到球第10次着地时共经过的路程为
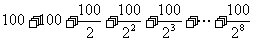
=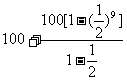
 300(米)
300(米)
答:共经过300米。
[例3] 一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一出生就在每年生日,到银行储蓄a元一年定期,若年利率为r保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁上大学时,将所有存款(含利息)全部取回,则取回的钱的总数为多少?
错解: 年利率不变,每年到期时的钱数形成一等比数列,那18年时取出的钱数应为以a为首项,公比为1+r的等比数列的第19项,即a19=a(1+r)18.
年利率不变,每年到期时的钱数形成一等比数列,那18年时取出的钱数应为以a为首项,公比为1+r的等比数列的第19项,即a19=a(1+r)18.
错因:只考虑了孩子出生时存入的a元到18年时的本息,而题目要求是每年都要存入a元.
正解:不妨从每年存入的a元到18年时产生的本息 入手考虑,出生时的a元到18年时变为a(1+r)18,
1岁生日时的a元到18岁时成为a(1+r)17,
2岁生日时的a元到18岁时成为a(1+r)16,
……
17岁生日时的a元到18岁时成为a(1+r)1,
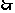 a(1+r)18+ a(1+r)17+ …+ a(1+r)1
a(1+r)18+ a(1+r)17+ …+ a(1+r)1
=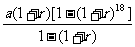
=
答:取出的钱的总数为 。
。
[例4]求数列 的前n项和。
的前n项和。
解:设数列的通项为an,前n项和为Sn,则 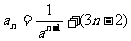
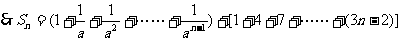
当 时,
时,
当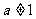 时,
时,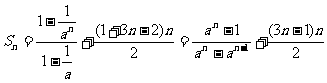
[例5]求数列 前n项和
前n项和
解:设数列的通项为bn,则
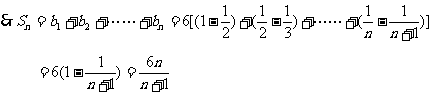
[例6]设等差数列{an}的前n项和为Sn,且 ,
,
求数列{an}的前n项和
解:取n =1,则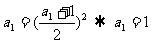
又由  可得:
可得: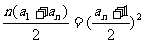
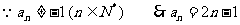

[例7]大楼共n层,现每层指定一人,共n人集中到设在第k层的临时会议室开会,问k如何确定能使n位参加人员上、下楼梯所走的路程总和最短。(假定相邻两层楼梯长相等)
解:设相邻两层楼梯长为a,则

当n为奇数时,取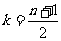 S达到最小值
S达到最小值
当n为偶数时,取 S达到最大值
S达到最大值
8.若一阶线性递推数列an=kan-1+b(k≠0,k≠1),则总可以将其改写变形成如下形式: (n≥2),于是可依据等比数列的定义求出其通项公式;
(n≥2),于是可依据等比数列的定义求出其通项公式;
7.对等差数列{an},当项数为2n时,S偶-S奇=nd;项数为2n-1时,S奇-S偶=a中(n∈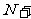 );
);
6.等差(或等比)数列的“间隔相等的连续等长片断和序列”(如a1+a2+a3,a4+a5+a6,a7+a8+a9…)仍是等差(或等比)数列;
5.若{an}、{bn}是等差数列,则{kan+bbn}(k、b是非零常数)是等差数列;若{an}、{bn}是等比数列,则{kan}、{anbn}等也是等比数列;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com