
3. 公理4:平行于同一条直线的两条直线平行.定理4:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
2. 空间两条直线的位置关系,包括:相交、平行、异面.
1. 平面的基本性质.公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.公理3:经过不在同一条直线上的三点,有且只有一个平面.推论1:经过一条直线和这条直线外的一点,,有且只有一个平面.推论2:经过两条相交直线,有且只有一个平面.推论3:经过两条平行直线,有且只有一个平面.
函数单调性或者求函数单调区间的求法。
(四)巩固练习:
1、下列函数中,在区间 上递增的是
( )
上递增的是
( )
(A)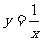 (B)
(B)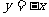 (C)
(C) (D)
(D)
2、设函数 是减函数,且
是减函数,且 ,下列函数中为增函数的是
( )
,下列函数中为增函数的是
( )
(A) (B)
(B)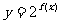 (C)
(C) (D)
(D)
3、已知 是定义在R上的偶函数,且
是定义在R上的偶函数,且 在(0,+∞)上是减函数,如果
在(0,+∞)上是减函数,如果 ,
,
 且
且 则有 ( )
则有 ( )
(A)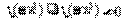 (B)
(B)
(C) (D)
(D)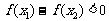
4、已知 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在 上为增函数,
上为增函数, ,则不等式
,则不等式 的解集为
( )
的解集为
( )
(A) (B)
(B) (C)
(C)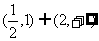 (D)
(D)
变题:设定义在[-2, 2]上的偶函数 在区间[0, 2]上单调递减,若
在区间[0, 2]上单调递减,若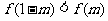 ,求实数m的取值范围。
,求实数m的取值范围。
5、(1)函数 的递增区间为___________;
的递增区间为___________;
(2)函数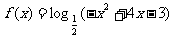 的递减区间为_________
的递减区间为_________
变题:已知 在[0, 1]上是减函数,则实数
在[0, 1]上是减函数,则实数 的取值范围是____。
的取值范围是____。
答案:1、D 2、C 3、C 4、D 变题: 5(1)
5(1) (2)
(2) 变题:(1,2)
变题:(1,2)
(三)例题分析:
例1.(1)求函数 的单调区间;
的单调区间;
(2)已知 若
若 试确定
试确定 的单调区间和单调性.
的单调区间和单调性.
解:(1)单调增区间为: 单调减区间为
单调减区间为 ,
,
(2)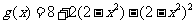
 ,
, ,
,
令  ,得
,得 或
或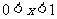 ,令
,令  ,
, 或
或
∴单调增区间为 ;单调减区间为
;单调减区间为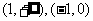 .
.
例2.设 ,
, 是
是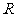 上的偶函数.
上的偶函数.
(1)求 的值;(2)证明
的值;(2)证明 在
在 上为增函数.
上为增函数.
解:(1)依题意,对一切 ,有
,有 ,即
,即
∴
 对一切
对一切 成立,则
成立,则 ,∴
,∴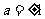 ,∵
,∵ ,∴
,∴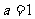 .
.
(2)设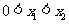 ,则
,则
 ,
,
由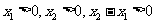 ,得
,得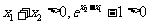 ,
, ,∴
,∴ ,
,
即 ,∴
,∴ 在
在 上为增函数.
上为增函数.
例3.若 为奇函数,且在
为奇函数,且在 上是减函数,又
上是减函数,又 ,则
,则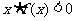 的解集为
的解集为 .
.
例4.已知函数 的定义域是
的定义域是 的一切实数,对定义域内的任意
的一切实数,对定义域内的任意 都有
都有 ,且当
,且当 时
时 ,
,
(1)求证: 是偶函数;(2)
是偶函数;(2) 在
在 上是增函数;(3)解不等式
上是增函数;(3)解不等式 .
.
解:(1)令 ,得
,得 ,∴
,∴ ,令
,令 ,得∴
,得∴ ,
,
∴ ,∴
,∴ 是偶函数.
是偶函数.
(2)设 ,则
,则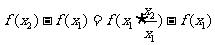
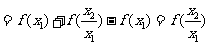
∵ ,∴
,∴ ,∴
,∴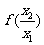
 ,即
,即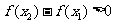 ,∴
,∴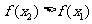
∴ 在
在 上是增函数.
上是增函数.
(3) ,∴
,∴ ,
,
∵ 是偶函数∴不等式
是偶函数∴不等式 可化为
可化为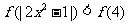 ,
,
又∵函数在 上是增函数,∴
上是增函数,∴ ,解得:
,解得: ,
,
即不等式的解集为 .
.
例5.函数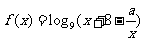 在
在 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
分析:由函数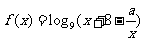 在
在 上是增函数可以得到两个信息:①对任意的
上是增函数可以得到两个信息:①对任意的 总有
总有 ;②当
;②当 时,
时, 恒成立.
恒成立.
解:∵函数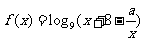 在
在 上是增函数,∴对任意的
上是增函数,∴对任意的 有
有 ,即
,即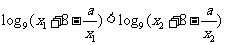 ,得
,得 ,即
,即 ,
,
∵ ,∴
,∴

 ,
,
∵ ,∴要使
,∴要使 恒成立,只要
恒成立,只要 ;
;
又∵函数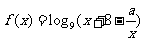 在
在 上是增函数,∴
上是增函数,∴ ,
,
即 ,综上
,综上 的取值范围为
的取值范围为 .
.
另解:(用导数求解)令 ,函数
,函数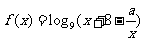 在
在 上是增函数,
上是增函数,
∴ 在
在 上是增函数,
上是增函数, ,
,
∴ ,且
,且 在
在 上恒成立,得
上恒成立,得 .
.
(二)主要方法:
1.讨论函数单调性必须在其定义域内进行,因此要研究函数单调性必须先求函数的定义域,函数的单调区间是定义域的子集;
2.判断函数的单调性的方法有:(1)用定义;(2)用已知函数的单调性;(3)利用函数的导数.
3.注意函数的单调性的应用;
4.注意分类讨论与数形结合的应用.
(一)主要知识:
1、函数单调性的定义;
2、判断函数单调性(求单调区间)的方法:
(1)从定义入手
(2)从导数入手
(3)从图象入手
(4)从熟悉的函数入手
(5)从复合函数的单调性规律入手
注:先求函数的定义域
3、函数单调性的证明:定义法;导数法。
4、一般规律
(1)若f(x),g(x)均为增函数,则f(x)+g(x)仍为增函数;
(2)若f(x)为增函数,则-f(x)为减函数;
(3)互为反函数的两个函数有相同的单调性;
(4)设 是定义在M上的函数,若f(x)与g(x)的单调性相反,则
是定义在M上的函数,若f(x)与g(x)的单调性相反,则 在M上是减函数;若f(x)与g(x)的单调性相同,则
在M上是减函数;若f(x)与g(x)的单调性相同,则 在M上是增函数。
在M上是增函数。
19. 半径分别为r和2r的两个质量不计的圆盘,共轴固定连结在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个质量为m的质点,小圆盘上绕有细绳.开始时圆盘静止,
质点处在水平轴O的正下方位置.现以水平恒力F拉细绳, 使两圆盘转动,若恒力 F=mg,两圆盘转过的角度θ=
时,质点m的速度最大.若圆盘转过的最大角度θ=π/3,则此时恒力F=
。
半径分别为r和2r的两个质量不计的圆盘,共轴固定连结在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个质量为m的质点,小圆盘上绕有细绳.开始时圆盘静止,
质点处在水平轴O的正下方位置.现以水平恒力F拉细绳, 使两圆盘转动,若恒力 F=mg,两圆盘转过的角度θ=
时,质点m的速度最大.若圆盘转过的最大角度θ=π/3,则此时恒力F=
。 
答案
 ,
,





[1D 2BC 3C
4BC 5B 6BCD7CD 8AC 9C 10B 11BCD]
18.一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有两个直径与细管内径相同的小球(可视为质点), A球的质量为m 1,B球的质量为m 2,它们沿环形圆管顺时针运动,经过最低点时的速度都为v 0.设A球运动到最低点时,B球恰好运动到最高点.若要此时两球作用于圆管的合外力为零,那么m 1、m 2、R与v
0应满足的关系式是
. 
答案:


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com