
3.对于命题“三个平面两两相交,有三条交线,则这三条交线互相平行或者相交于同一点.”要会证明.
2.面面平行也是推导线面平行的重要手段;还要注意平行与垂直的相互联系,如:如果两个平面都垂直于同一条直线,则这两个平面平行;如果两条直线都垂直于一个平面,则这两条直线平行等.在证明平行时注意线线平行、线面平行及面面平行的判定定理和性质定理的反复运用.
1.两个平面的位置关系关系的判定关键看有没有公共点.
4.二面角的有关概念(从一条直线出发的两个半平面所组成的图形叫做二面角)与运算; 二面角的平面角(以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角),二面角的平面角的常见作法(定义法、三垂线定理及逆定理法、垂面法等).
3.理解并掌握空间两个平面垂直的定义(一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直);判定定理(如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直)和性质定理(如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面).
2.理解并掌握空间两个平面平行的定义;掌握空间两个平面平行判定定理(如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行)和性质定理(如果两个平行平面同时和第三个平面相交,那么它们的交线平行).
1.空间两个平面的位置关系(有交点的是相交;没交点的是平行).
7.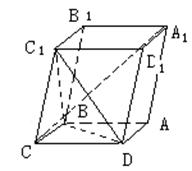 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且
如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且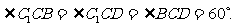
(1)
证明C1C ;
;
(2)
当 的值为多少时,能使A1C
的值为多少时,能使A1C 平面C1BD?请给出证明.
平面C1BD?请给出证明.
§6.3平面与平面之间的位置关系
6.已知两个全等的矩形ABCD 和ABEF 不在同一平面内,M 、N 分别在它们的对角线AC ,BF 上,且CM=BN ,
求证:MN∥ 平面BCE .
5.点P 、Q 、R 、S 分别是空间四边形ABCD 四边的中点,则:当AC 时,四边形
时,四边形 PQRS 是______形;当AC=BD 时,四边形PQRS
是____形.
PQRS 是______形;当AC=BD 时,四边形PQRS
是____形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com