
4.二面角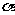 -
-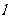 -
- 内一点P,分别作两个面的垂线PA、PB,A、B为垂足.已知PA=3,PB=2,∠APB=60°求
内一点P,分别作两个面的垂线PA、PB,A、B为垂足.已知PA=3,PB=2,∠APB=60°求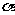 -
-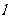 -
- 的大小及P到
的大小及P到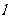 的距离.
的距离.
3. 在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是AB和AD的中点,则点A1到平面EFB1D1的距离为
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是AB和AD的中点,则点A1到平面EFB1D1的距离为
2.异面直线a , b所成的角为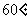 ,过空间一定点P,作直线
,过空间一定点P,作直线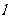 ,使
,使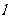 与a ,b 所成的角均为
与a ,b 所成的角均为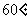 ,这样的直线
,这样的直线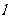 有
条.
有
条.
1.在平面角为600的二面角 内有一点P,P到α、β的距离分别为PC=2cm,PD=3cm,则P到棱
内有一点P,P到α、β的距离分别为PC=2cm,PD=3cm,则P到棱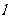 的距离为____________.
的距离为____________.
[例1] 平面 外有两点A,B,它们与平面
外有两点A,B,它们与平面 的距离分别为a,b,线段AB上有一点P,且AP:PB=m:n,则点P到平面
的距离分别为a,b,线段AB上有一点P,且AP:PB=m:n,则点P到平面 的距离为_________________.
的距离为_________________.
错解: .
.
错因:只考虑AB在平面同侧的情形,忽略AB在平面两测的情况.
正解: .
.
[例2]与空间四边形ABCD四个顶点距离相等的平面共有______个.
错解:4个.
错因:只分1个点与3个点在平面两侧.没有考虑2个点与2个点在平面两侧.
正解:7个.
[例3]一个盛满水的三棱锥形容器,不久发现三条侧棱上各有一个小洞D、E、F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛原来水的( )
 A.
A.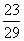 B.
B.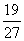 C.
C. D.
D.
错解:A、B、C.由过D或E作面ABC的平行面,所截体计算而得.
正解:D.
当平面EFD处于水平位置时,容器盛水最多



最多可盛原来水得1-
[例4]斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB、AC都成450角,求这个三棱柱的侧面积.
错解:一是不给出任何证明,直接计算得结果;二是作直截面的方法不当,即“过BC作平面与AA1垂直于M”;三是由条件“∠A1AB=∠A1AC ∠AA1在底面ABC上的射影是∠BAC的平分线”不给出论证.
∠AA1在底面ABC上的射影是∠BAC的平分线”不给出论证.
正解:过点B作BM⊥AA1于M,连结CM,在△ABM和△ACM中,∵AB=AC,∠MAB=∠MAC=450,MA为公共边,∴△ABM≌△ACM,∴∠AMC=∠AMB=900,∴AA1⊥面BHC,即平面BMC为直截面,又BM=CM=ABsin450= a,∴BMC周长为2x
a,∴BMC周长为2x a+a=(1+
a+a=(1+ )a,且棱长为b,∴S侧=(1+
)a,且棱长为b,∴S侧=(1+ )ab
)ab
[例5]已知CA⊥平面α,垂足为A;AB  α,BD⊥AB,且BD与α成30°角;AC=BD=b,AB=a.求C,D两点间的距离.
α,BD⊥AB,且BD与α成30°角;AC=BD=b,AB=a.求C,D两点间的距离.
解 : 本题应分两种情况讨论:
(1)如下左图.C,D在α同侧:过D作DF⊥α,垂足为F.连BF,则 于是
于是 .
.
 根据三垂线定理BD⊥AB得BF⊥AB.
根据三垂线定理BD⊥AB得BF⊥AB.
在Rt△ABF中,AF=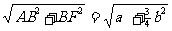
过D作DE AC于E,则DE=AF,AE=DF=
AC于E,则DE=AF,AE=DF=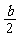 .所以EC=AC-AE= b-
.所以EC=AC-AE= b-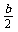 =
= .故
.故
CD=
(2)如上右图.C,D在α两侧时:同法可求得CD=
 点 评: 本题是通过把已知量与未知量归结到一个直角三角形中,应用勾股定理来求解.
点 评: 本题是通过把已知量与未知量归结到一个直角三角形中,应用勾股定理来求解.
[例6]如图,在棱长为1的正方体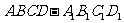 中,
中, 是侧棱
是侧棱 上的一点,
上的一点, .
.
(1)试确定 ,使得直线
,使得直线 与平面
与平面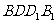 所成角的正切值为
所成角的正切值为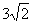 ;
;
(2)在线段 上是否存在一个定点
上是否存在一个定点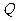 ,使得对任意的
,使得对任意的 ,
, 在平面
在平面 上的射影垂直于
上的射影垂直于 .
.
并证明你的结论.
解:解法一(1)连AC,设AC与BD相交于点O,AP与平面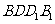 相交于点,,连结OG,因为
相交于点,,连结OG,因为
 PC∥平面
PC∥平面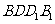 ,平面
,平面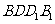 ∩平面APC=OG,
∩平面APC=OG,
故OG∥PC,所以,OG= PC=
PC=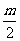 .
.
又AO⊥BD,AO⊥BB1,所以AO⊥平面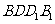 ,
,
故∠AGO是AP与平面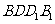 所成的角.
所成的角.
在Rt△AOG中,tan AGO=
AGO=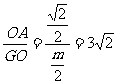 ,即m=
,即m= .
.
所以,当m= 时,直线AP与平面
时,直线AP与平面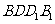 所成的角的正切值为
所成的角的正切值为 .
.
(2)可以推测,点Q应当是AICI的中点O1,因为
D1O1⊥A1C1, 且 D1O1⊥A1A ,所以 D1O1⊥平面ACC1A1,
又AP 平面ACC1A1,故 D1O1⊥AP.
平面ACC1A1,故 D1O1⊥AP.
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直。
 解法二:(1)建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1)
解法二:(1)建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1)
所以
又由 知,
知, 为平面
为平面 的一个法向量。
的一个法向量。
设AP与平面 所成的角为
所成的角为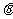 ,则
,则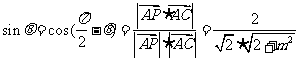 。依题意有
。依题意有 解得
解得 。故当
。故当 时,直线AP与平面
时,直线AP与平面 所成的角的正切值为
所成的角的正切值为 。
。
(2)若在A1C1上存在这样的点Q,设此点的横坐标为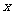 ,则Q(x,1-
,则Q(x,1-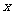 ,1),
,1),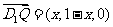 。依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP,等价于D1Q⊥AP
。依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP,等价于D1Q⊥AP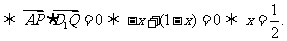 即Q为A1C1的中点时,满足题设要求。
即Q为A1C1的中点时,满足题设要求。
[例7]在梯形ABCD中,∠ADC=90°,AB∥DC,AB=1,DC=2, ,P为平面ABCD外一点,PAD是正三角形,且PA⊥AB,
,P为平面ABCD外一点,PAD是正三角形,且PA⊥AB,
求:(1)平面PBC和平面PAD所成二面角的大小;
(2)D点到平面PBC的距离.
 解: (1)设AD∩BC=E,可知PE是平面PBC和平面PAD的交线,依题设条件得PA=AD=AE,则∠EPD=90°,PD⊥PE
解: (1)设AD∩BC=E,可知PE是平面PBC和平面PAD的交线,依题设条件得PA=AD=AE,则∠EPD=90°,PD⊥PE
又PA⊥AB,DA⊥AB,故AB⊥平面PAD.
∵ DC∥AB,∴ DC⊥平面PAD.
由PE⊥PC得PE⊥PD,∠DPC是平面PBC与平面PAD所成二面角的平面角. ,DC=2,tan
,DC=2,tan ,
,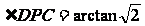 .
.
(2)由于PE⊥PD,PE⊥PC,故PE⊥平面PDC,
因此平面PDC⊥平面PBC,
作DH⊥PC,H是垂足,则DH是D到平面PBC的距离.
在Rt△PDC中, ,DC=2,
,DC=2, ,
, .
.
平面PBC与平面PAD成二面角的大小为arctan ,D到平面PBC的距离为
,D到平面PBC的距离为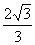 .
.
[例8] 半径为1的球面上有A、B、C三点,A与B和A与C的 球面距离都是
球面距离都是 ,B与C的球面距离是
,B与C的球面距离是 ,求过A、B、C三点的截面到球心O距离.
,求过A、B、C三点的截面到球心O距离.
分析 : 转化为以球心O为顶点,△ABC为底面的三棱锥问题解决.
由题设知△OBC是边长为1的正三角形,△AOB和△AOC是腰长为1的全等的等腰三角形.
取BC中点D,连AD、OD,易得BC⊥面AOD,进而得面AOD⊥面ABC,过O作OH⊥AD于H,则OH⊥面ABC,OH的长即为
所求,在Rt 中,AD=
中,AD=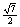 ,故在Rt
,故在Rt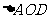 ,OH=
,OH=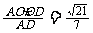
点评: 本题若注意到H是△ABC的外心,可通过解△ABC和△AHO得OH.或利用体积法.
5.要注意距离和角在空间求值中的相互作用,以及在求面积和体积中的作用.
4.球面上两点间的距离是指经过这两点的球的大圆的劣弧的长,关键在于画出经过两点的大圆以及小圆.
3.空间距离的计算一般将其转化为两点间的距离.求点到平面距离时,可先找出点在平面内的射影(可用两个平面垂直的性质),也可用等体积转换法求之.另外要注意垂直的作用.球心到截面圆心的距离由勾股定理得
2.求二面角大小时,关键是找二面角的平面角,可充分利用定义法或垂面法等.
1.求空间角的大小时,一般将其转化为平面上的角来求,具体地将其转化为某三角形的一个内角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com