
8.在△ABC中,3sinA+4cosB=6,4sinB+3cosA=1,则C等于 ( )
A.30° B.150° C.30°或150° D.60°或120°
解析:已知两式两边分别平方相加,得
25+24(sinAcosB+cosAsinB)=25+24sin(A+B)=37,
∴sin(A+B)=sinC=,∴C=30°或150°.
当C=150°时,A+B=30°,此时3sinA+4cosB<3sin30°+4cos0°=,这与3sinA+4cosB=6相矛盾,∴C=30°.
答案:A
7.已知A、B均为钝角,且sinA=,sinB=,则A+B等于 ( )
A. B. C.或 D.
解析:由已知可得cosA=-,cosB=-,
∴cos(A+B)=cosAcosB-sinAsinB=,
又∵<A<π,<B<π,
∴π<A+B<2π,∴A+B=.
答案:B
6.已知cos=,x∈.
(1)求sinx的值;
(2)求sin的值.
解:(1)法一:因为x∈,
所以x-∈,
sin= =.
sinx=sin[+]
=sin(x-)cos+cos(x-)sin
=×+×=.
法二:由题设得cosx+sinx=,
即cosx+sinx=.
又sin2x+cos2x=1,
从而25sin2x-5sinx-12=0,
解得sinx=或sinx=-.
因为x∈,所以sinx=.
(2)因为x∈,
故cosx=-=-=-.
sin2x=2sinxcosx=-,
cos2x=2cos2x-1=-.
所以sin=sin2xcos+cos2xsin
=-.
|
题组三 |
给值求角问题 |
5.已知α为钝角,且sin(α+)=,则cos(α+)的值为 ( )
A. B. C.- D.
解析:∵α为钝角,且sin(α+)=,
∴cos(α+)=-,
∴cos(α+)=cos[(α+)+]=cos(α+)cos-sin(α+)sin=(-)·-·=-.
答案:C
4.sin(-x)=,则sin2x的值为 ( )
A. B. C. D.
解析:∵sin(-x)=,
∴cosx-sinx=(cosx-sinx)=.
∴cosx-sinx=.
∴(cosx-sinx)2=1-sin2x=,
∴sin2x=.
答案:A
3.(2010·辽宁模拟)已知α、β均为锐角,且tanβ=,则tan(α+β)=________.
解析:∵tanβ=,
∴tanβ==tan(-α).
又∵α、β均为锐角,∴β=-α,即α+β=,
∴tan(α+β)=tan=1.
答案:1
|
题组二 |
给值求值问题 |
2.+2的化简结果是 ( )
A.4cos4-2sin4 B.2sin4
C.2sin4-4cos4 D.-2sin4
解析:原式=+2
=2|cos4|+2|sin4-cos4|,
∵<4<,∴cos4<0,sin4<cos4.
∴原式=-2cos4+2(cos4-sin4)=-2sin4.
答案:D
1.的值是 ( )
A. B. C. D.
解析:原式=
=
==.
答案:C
20. (本小题满分16分)
(本小题满分16分)
已知函数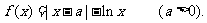
(1)若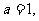 求
求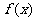 的单调区间及
的单调区间及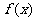 的最小值;
的最小值;
(2)若 ,求
,求
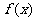 的单调区间;
的单调区间;
(3)试比较) 的大小,
的大小,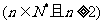 ,并证明你的结论。
,并证明你的结论。
19.(本小题满分16分)
公差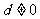 的等差数列
的等差数列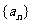 的前
的前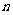 项和为
项和为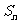 ,已知
,已知 ,
,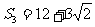 .
.
(Ⅰ)求数列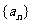 的通项公式
的通项公式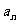 及其前
及其前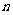 项和
项和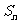 ;
;
(Ⅱ)记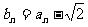 ,若自然数
,若自然数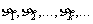 满足
满足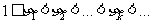 ,并且
,并且
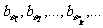 成等比数列,其中
成等比数列,其中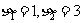 ,求
,求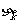 (用
(用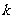 表示);
表示);
(Ⅲ)记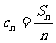 ,试问:在数列
,试问:在数列 中是否存在三项
中是否存在三项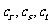
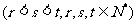 恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com