
17.简单随机抽样:设一个总体的个体数为N.如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样 ⑴用简单随机抽样从含有N个个体的总体中抽取一个容量为
⑴用简单随机抽样从含有N个个体的总体中抽取一个容量为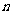 的样本时,每次抽取一个个体时任一个体被抽到的概率为
的样本时,每次抽取一个个体时任一个体被抽到的概率为 ;在整个抽样过程中各个个体被抽到的概率为
;在整个抽样过程中各个个体被抽到的概率为 ; ⑵简单随机抽样的特点是,逐个抽取,且各个个体被抽到的概率相等; ⑶简单随机抽样方法,体现了抽样的客观性与公平性,是其他更复杂抽样方法的基础.(4).简单随机抽样的特点:它是不放回抽样;它是逐个地进行抽取;它是一种等概率抽样
; ⑵简单随机抽样的特点是,逐个抽取,且各个个体被抽到的概率相等; ⑶简单随机抽样方法,体现了抽样的客观性与公平性,是其他更复杂抽样方法的基础.(4).简单随机抽样的特点:它是不放回抽样;它是逐个地进行抽取;它是一种等概率抽样
16.方差的性质: ① ;②若ξ-B(n,p),则
;②若ξ-B(n,p),则 np(1-p)
np(1-p)
15. 标准差: 的算术平方根
的算术平方根 叫做随机变量ξ的标准差,记作
叫做随机变量ξ的标准差,记作 .
.
14. 方差:
 =
=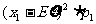 +
+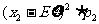 +…+
+…+ +….
+….
13.若ξ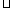 B(n,p),则Eξ=np
B(n,p),则Eξ=np 
12. 期望的一个性质: 
10. 数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平 
11 平均数、均值:在有限取值离散型随机变量ξ的概率分布中,令
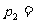 …
… ,则有
,则有
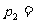 …
… ,
,

 …
… ,所以ξ的数学期望又称为平均数、均值
,所以ξ的数学期望又称为平均数、均值

9.数学期望: 一般地,若离散型随机变量ξ的概率分布为
|
ξ |
x1 |
x2 |
… |
xn |
… |
|
P |
p1 |
p2 |
… |
pn |
… |
则称 
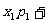
 …
… … 为ξ的数学期望,简称期望.
… 为ξ的数学期望,简称期望.
8.几何分布: g(k,p)= 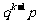 ,其中k=0,1,2,…,
,其中k=0,1,2,…,
 .
.
|
ξ |
1 |
2 |
3 |
… |
k |
… |
|
P |
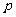 |
 |
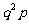 |
… |
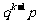 |
… |
7.二项分布:ξ-B(n,p),并记 =b(k;n,p).
=b(k;n,p).
|
ξ |
0 |
1 |
… |
k |
… |
n |
|
P |
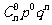 |
 |
… |
 |
… |
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com