
4.
 图中山地年降水量
图中山地年降水量
A. 随海拔升高而递减
B.与山地气温垂直变化一致
C.最大值所在海拔高度不同
D.垂直变化最大的是山地①
3. 臭氧总量减少直接导致
A. 太阳紫外线辐射减小
B. 平流层气温降低
C. 酸雨区面积缩小
D. 地面辐射强度减弱
图3显示中国不同地区山地年降水量从山麓到山顶的变化。读图3,回答第4、5。
2. 随年份的推移,臭氧总量
A. 最大值所在位置南移
B. 随维度的增高而递减
C. 在高纬地区递减明显
D. 随大气CO2浓度而增
1.Ⅰ区太阳年辐射总量比Ⅳ区高,主要因为Ⅰ区
A. 夏季大气逆辐射强
B. 年平均气温比较高
C. 正午太阳高度角大
D. 天气晴朗且海拔高
臭氧层保护是当今全球最重要的环保议题之一。图2反映了9月份30°S-80°S平流层臭氧总量多年变化状况 读图2,回答2、3题。
读图2,回答2、3题。
21.(本小题满分14分)
已知二次函数 的导函数的图像与直线
的导函数的图像与直线 平行,且
平行,且 在
在 =-1处取得最小值m-1(m
=-1处取得最小值m-1(m ).设函数
).设函数
(1)若曲线 上的点P到点Q(0,2)的距离的最小值为
上的点P到点Q(0,2)的距离的最小值为 ,求m的值
,求m的值
(2)  如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
[解析](1)设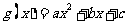 ,则
,则 ;
;
又 的图像与直线
的图像与直线 平行
平行


又 在
在 取极小值,
取极小值,
 ,
, 
 ,
, 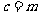 ;
;
 ,
设
,
设
则


 ;
; 

(2)由 ,
,
得 

当 时,方程
时,方程 有一解
有一解 ,函数
,函数 有一零点
有一零点 ;
;
当 时,方程
时,方程 有二解
有二解 ,若
,若 ,
, ,
,
函数 有两个零点
有两个零点 ;若
;若 ,
,
 ,函数
,函数 有两个零点
有两个零点 ;
;
当 时,方程
时,方程 有一解
有一解 ,
,  , 函数
, 函数 有一零点
有一零点


20.(本小题满分14分)
已知点(1, )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前n项和为
的前n项和为 ,数列
,数列
 的首项为c,且前n项和
的首项为c,且前n项和 满足
满足 -
- =
= +
+ (n
(n 2).
2).
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若数列{ 前n项和为
前n项和为 ,问
,问 >
> 的最小正整数n是多少?
的最小正整数n是多少?
[解析](1) ,
,


 ,
,
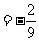 ,
,
 .
.
又数列 成等比数列,
成等比数列, ,所以
,所以  ;
;
又公比 ,所以
,所以
 ;
;


又 ,
, ,
,  ;
;
数列 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列, ,
, 
当 ,
,  ;
;
 (
( );
);
(2)


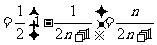 ;
; 

由 得
得 ,满足
,满足 的最小正整数为112.
的最小正整数为112.
19.(本小题满分14分)
已知椭圆G的中心在坐标原点,长轴在 轴上,离心率为
轴上,离心率为 ,两个焦点分别为
,两个焦点分别为 和
和 ,椭圆G上一点到
,椭圆G上一点到 和
和 的距离之和为12.圆
的距离之和为12.圆 :
:
 的圆心为点
的圆心为点 .
.
(1)求椭圆G的方程
(2)求 的面积
的面积
(3)问是否存在圆 包围椭圆G?请说明理由.
包围椭圆G?请说明理由.
[解析](1)设椭圆G的方程为: (
( )半焦距为c;
)半焦距为c;
则 , 解得
, 解得 ,
, 
所求椭圆G的方程为: .
.


(2 )点 的坐标为
的坐标为

(3)若 ,由
,由 可知点(6,0)在圆
可知点(6,0)在圆 外,
外,
若 ,由
,由 可知点(-6,0)在圆
可知点(-6,0)在圆 外;
外;
 不论K为何值圆
不论K为何值圆 都不能包围椭圆G.
都不能包围椭圆G.
18.(本小题满分13分)
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.

[解析](1)由茎叶图可知:甲班身高集中于 之间,而乙班身高集中于
之间,而乙班身高集中于 之间。因此乙班平均身高高于甲班;
之间。因此乙班平均身高高于甲班;
(2) 
甲班的样本方差为
 =57
=57
(3)设身高为176cm的同学被抽中的事件为A;
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173) (181,176)
(181,178) (181,179) (179,173) (179,176) (179,178) (178,173)
(178, 176) (176,173)共10个基本事件,而事件A含有4个基本事件;
 ;
;
17.(本小题满分13分)
某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积
(3)证明:直线BD 平面PEG
平面PEG

[解析](1)侧视图同正视图,如下图所示.

(2)该安全标识墩的体积为:


(3)如图,连结EG,HF及 BD,EG与HF相交于O,连结PO.
由正四棱锥的性质可知, 平面EFGH ,
平面EFGH , 
又
 平面PEG
平面PEG
又
 平面PEG;
平面PEG; 


16.(本小题满分12分)
已知向量 与
与 互相垂直,其中
互相垂直,其中
(1)求 和
和 的值
的值
(2)若 ,
,
 ,求
,求 的值
的值
[解析](1) ,
, ,即
,即
又∵ , ∴
, ∴ ,即
,即 ,∴
,∴
又  ,
,
(2) ∵


 ,
, ,即
,即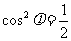
又 
 , ∴
, ∴


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com